《线性代数》中“特征值与特征向量”的教学创新探析

张明

（中国劳动关系学院，北京 100048）

线性代数（Linear Algebra）是数学学科的一个重要分支，它的研究对象是向量、向量空间（或称线性空间）、线性变换和有限维的线性方程组。但是由于线性代数课程的理论性、抽象性及学生所学知识的有限性，我们发现，同学们很难理解这些名词，更谈不上深层次的应用了，特别是对文科专业的学生而言。其中，特征值与特征向量就是一个大家公认的难点。那么我们换个视角，不从科学的、严谨的角度来学习，而是采用“形象的”的方式先掌握住它，然后再从更高、更深的层次来理解、应用，也是一条很不错的学习路径与方法。

关于特征值与特征向量，有观点认为是大数学家莱昂哈德·欧拉（Leonhard Euler）在化三元二次型到主轴的著作里隐含出现了特征方程概念； 也有学者认为是约瑟夫·拉格朗日（Joseph-Louis Lagrange）在思考和处理六大行星运动的微分方程组时，首先明确给出特征方程的概念；现在，更多的观点把它归功于矩阵论的创立者、第一个把矩阵作为一个独立的数学概念提出来的数学家凯莱（A.Cayley）。下面我们就先从特征值与特征向量的定义与性质、矩阵的相似对角化和对称矩阵的正交对角化从“形象的”角度谈起。

1 特征值与特征向量的定义与计算

在《线性代数》教材中：设A 为n 阶方阵，若存在数λ 和n 为非零向量α≠0，使Aα=λα，则称λ 是方阵A的特征值，α 是方阵A 的属于特征值λ 的特征向量；矩阵λE-A 称为方阵A 的特征矩阵；|λE-A|是λ 的n 次多项式，称为方阵A 的特征多项式；|λE-A|=0 称为方阵A 的特征方程。比如，对于方阵而言，对于显然有Aα=λα，所以5 为A 有一个特征值，为A 的属于特征值5 的特征向量。

通过观察，可以发现特征方程|λE-A|=0 的解即为方阵A 的特征值λ0，此处我们还发现，由于|λE-A|=0是λ 的n 次多项式，从而特征方程|λE-A|=0 有个n 根（包括重根），也就是说n 阶方阵A 有n 个特征根，而相应的特征向量α 为方程组（λ0E-A）x=0 的非零解。此处可以这样理解（以下仅是借助于老旧社会的一些名词，没有任何崇尚或推广封建余孽思想的含义于其中，其目的是为了不用专业术语来解释相关理论）：

方阵可以理解为封建社会的富人，他们一般都是肚圆肠肥，身高几乎等于圆乎乎肚子的直径，也就是个好方的富人，我们称之为方阵； 而富人们一般儿孙很多，n 阶富人A 就有了n 个儿子，也就是n 阶方阵A 有n 个特征根；富人的儿子们总会娶妻纳妾，大儿子λ1的妻就是方程组（λ1E-A）x=0 的基础解系，妾就是方程组（λ1E-A）x=0 的所有解（基础解系的线性组合，也就是属于特征值λ1的所有特征向量）。

总结，n 阶方阵A 有n 个特征根，也就是n 阶富人有n 个儿子，由于其财大气粗，每个儿子妻妾成群，方阵A 有属于不同特征根的特征向量就是相应方程组（λ0E-A）x=0 的所有解，也就是每个儿子成群的妻妾们。

2 矩阵的相似对角化问题

设A 为n 阶方阵，若存在n 阶可逆阵P，使P-1AP=Λ 和其中Λ 为对角矩阵，称Λ 与对角矩阵相似，也称方阵可以相似对角化。此时，设且P-1AP=Λ，有AP=PΛ，将矩阵P 分块，得A（α1，α2，···αn）=（α1，α2，···，αn）Λ，从而有Aαi=λαi（i=1，2，···，n）。不难发现，如果存在n 阶可逆阵P，使得P-1AP=Λ，那么对角矩阵就是矩阵A 的特征值，而可逆矩阵P，就是每一个特征值相应特征向量按列排所得。

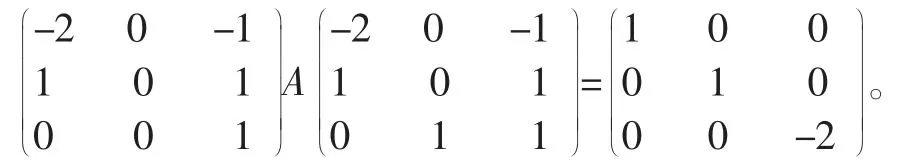
总结，n 阶富人想让儿媳妇们把自己的家A 打扫、收拾得井井有条、干干净净于是他发动儿媳妇们α1，α2，···αn把家里里外外都认真的打扫了一遍（α1，α2，···αn）TA（α1，α2，···αn），于是，这个家就井井有条，儿子们也就规规矩矩的了，而这恰好是方阵为相似对角化的过程与计算。

此处还有一个问题，是随随便便一位富人就可以做到这件事情的吗？答案当然是否定的，所以教材上有这样的定理或者结论：

定理1：n 阶矩阵A 和对角阵相似当且仅当A 有n个线性无关的特征向量。

那换个说法，富人的n 个儿媳妇彼此间互不影响的情况下，才能够顺顺利利的把家打扫的一尘不染，干干净净。毕竟，万一有两个儿媳妇是亲戚，串通好偷奸耍滑，这家就没法打扫了嘛！

定理2：如果A 有n 个不同的特征值，则A 和对角阵相似。因为，矩阵A 的属于不同特征值的特征向量是线性无关的。（证明略）

此时，富人家的儿子们性格迥异完全不同，都一心想着把家来打扫，妻子们必然也会去把家收拾干净、利索的。

3 对称矩阵的正交对角化

设A 为n 阶对称矩阵，若存在n 阶正交矩阵Q，使QTAQ=Λ,其中Λ 为对角矩阵，称对称矩阵A 可以正交对角化。此时正交矩阵的Q 特点是QQT=E，即QT=Q-1，根据相似对角化的过程，设对称矩A 阵的特征值λ1，λ2，···，λn，相应的特征向量为α1，α2···，αn，运用施密特正交化方法，将向量组α1，α2，···αn 正交化得β1，β2，···，βn，再将其单位化得ε1，ε2，···，εn，令Q=（ε1，ε2，···，εn）显然有QQT=E，且即。

总结：n 阶对称矩阵A，也就是工工整整的富人想让知书达理、美丽大方的儿媳妇们把自己的家打扫、收拾的很整洁 但儿媳们的受教育程度参差不齐，于是富人先让儿媳妇们α1，α2，···，αn 参加培训，培训学习之后就各个美丽大方、知书达理、精通琴棋书画，ε1，ε2，···，εn，此时

家就被打扫得很整洁，而这正好又是对称矩阵A正交对角化的过程的体现。

4 结语

以上内容属于从生活实例的角度来看、解释严谨的数学知识，其目的仅是为了学生更容易接受、理解抽象、晦涩的数学知识，不涉及任何的歧视及封建思想的宣扬。

毕竟《线性代数》的基本理论、基本知识高度抽象，又具有严密的逻辑性，再由于学生学习、接触的知识面，单纯地从数学或者专业的知识角度去完全理解、掌握所有的知识点是非常困难的，并且在这个过程中，会有一些学生选择放弃，这是我们所不愿意看到的，所以尝试着从非专业、非科学的角度来解释、讲解晦涩的知识。这仅是一种尝试，失败与成功还是要看其效果。