一种基于频率响应函数的刚体惯性参数改进识别方法

何宇翔，王 彤，张丽君

(1.南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016;2.中车唐山机车车辆有限公司，唐山 063000)

刚体惯性参数包括质量、质心、转动惯量、惯性积，其识别方法主要包括落体法、三线摆法、基于三维数字模型的数值计算法及基于频响函数的振动试验模态分析法等[1-2]。

落体法主要用于测量小部件的惯性参数，且识别精度较差[3]，三线摆法具有较高的精度，但它的缺点是实验设备复杂，安全性差[4]；三维数字模型法通过建立准确的三维模型计算刚体惯性参数，但对于复杂结构，建立准确的三维模型的难度不言而喻[5-6]。基于频响函数和振动试验模态分析的刚体惯性参数辨识方法具有简单、快速和精度高等优点，可很大程度上避免上述问题的发生。振动试验模态分析方法主要包括模态模型法(Modal Method,MM)、质量线法(Inertia Restrain Method,IRM)和直接物理参数识别法(Direct Physical Parameter Identification Method,DPPIM)。

模态模型法(MM)基于刚体模态对刚体质量矩阵具有正交性[7]，达到求解惯性参数的目的。刚体模态振型通过频率响应函数获得，将其质量归一化后，结合响应点坐标转换矩阵求得刚体质量矩阵。常用的方法是Conti-Bretl法[8](C-B法)和Toivola-Nuutila法[9](T-N法)。C-B法要求求出所有6阶刚体模态之后，建立刚体振型矩阵，T-N法只需要4阶刚体振型，通过解方程组求得所有惯性参数。为了得到理想的刚体振型，必须人为地添加理想的弹簧约束。然而在实际测试中，理想的边界条件几乎无法做到。此外，实际实验中很难准确地获得4阶理想的刚体振型[10]。一次识别所有参数的精度很难保证。

DPPIM法基于频率响应函数，可一次性得到刚体全部10个惯性参数。研究显示该法受噪声和弹性模态影响很大[11]，且最终的求解结果是6×6阶矩阵，使用最小二乘法可能会放大误差[12]。质量线法(IRM)它将质量作为已知的参数，利用质心与转动惯量相互独立的性质，分步求解剩余的9个参数。质量线法矩阵计算规模较小，最终得到的是一个3×1的质心坐标向量和一个6×1的惯性张量向量，是一些商业化软件采用的方法。仿真和实验结果表明，IRM在较大噪声输入时仍具有较高识别精度。然而，在实际应用中，质量参数往往未知，且对大型结构称重也很难实现。

由于DPPIM法和IRM法单独使用都具有一定的局限性，本文提出了一种将两种方法组合使用的改进型惯性参数识别方法，即先利用直接参数识别法识别质量，再使用质量线法识别剩余9个参数。

1 惯性参数识别原理

1.1 直接参数识别法(DPPIM)

刚体的质量矩阵可以表示为

(1)

刚体振动方程

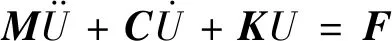
(2)

刚度和阻尼很小时，相关的两项可以忽略不计，振动方程变为

(3)

在坐标系中，第i(i=1,2,…n,其中n为激励点总个数)个激励点的坐标是(xi,yi,zi)，该处的激励力fi在原点O处产生的激振力是

(4)

(5)

由式(5)可知，含有n个激励点和m个响应点组合而成的加速度响应矩阵如式(6)所示

(6)

(7)

由式(4)，n个激励点在坐标原点产生的激振力为

FO,6×n=[FO1…FOn]=

(8)

由式(3)，由n个激励点和m个响应点作用下的刚体振动方程为

(9)

将式(7)和式(8)代入式(9)，得

(10)

式(10)两端同时右乘f-1，得

(11)

H是由实验测得的激励点和响应点之间的加速度频响函数，式(11)使用最小二乘法来计算矩阵M，因此激振力坐标转换矩阵W的秩不能小于6，即激励点总个数n≥6。

由最小二乘方法，可以得刚体的质量矩阵M

M=W(RTR)T(RTHHTR)-1(RTR)

(12)

1.2 质量线法(IRM)

IRM将质量作为已知参数，求出质心、转动惯量和惯性积。由式(9)获得的IRM法计算公式

(13)

由于质心与转动惯量和惯性积相互独立，因此可分步识别。由式(14)识别质心

(14)

由式(15)识别转动惯量和惯性积

(15)

对由式(15)求得的转动惯量和惯性积应用平行轴定理，将其转化到对质心所在坐标轴的转动惯量和惯性积，再组成惯性张量矩阵，如式(16)所示，求解其特征值与特征向量即可得到主转动惯量和3个惯性主轴关于固定坐标系坐标轴夹角的方向余弦。

(16)

2 直接参数识别法和质量线法的对比仿真

分别应用直接参数识别法、质量线法和模态模型法对一个平板进行仿真试验。平板的几何模型如图1所示。

图1 几何模型Fig.1 Geometry model

如果惯性主轴太靠近坐标轴，很小绝对误差将导致较大的相对误差。因此，将平板是沿(2,2,2)的方向移动。板的惯性参数的参考值如表1所示，第一阶弹性模态振型如图2所示。

表1 各参数的参考值(m=9.48 kg)Tab.1 Reference value of each parameter(m=9.48 kg)

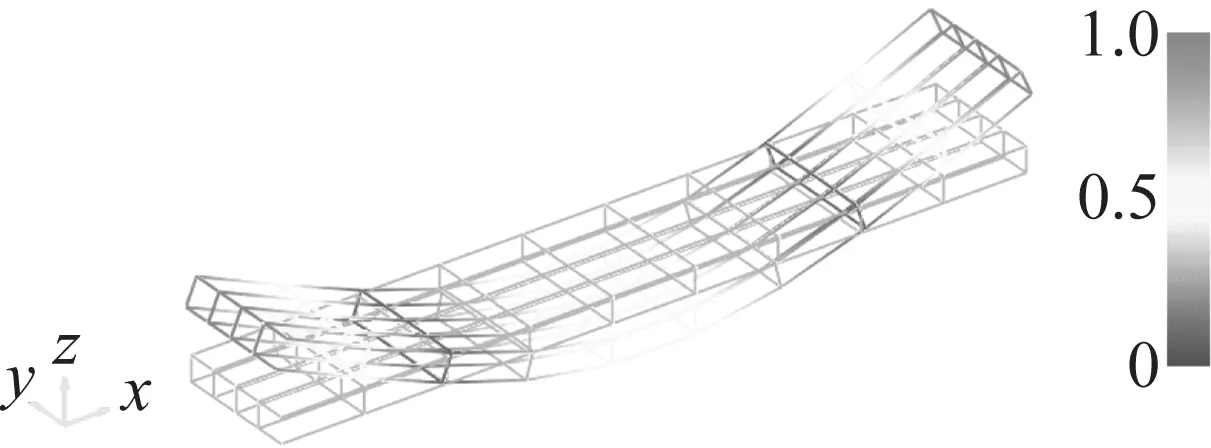
图2 第一阶弹性模态振型Fig.2 The first elastic mode

2.1 响应点位于顶角处

在刚体顶角节点 1、10、91、100上设置三方向响应点，响应点坐标变换矩阵条件数为19.6。激励点为节点1X+，10Y+，41Y+，91Z+，60Z+，100Z+。激励点坐标转换矩阵条件数为24.7。弹簧分布位于顶角上节点1，10，41，50的Z方向，每个弹簧的刚度是20 kN/m。

图3 响应点在顶角处的频响函数Fig.3 Frequency response functions of corner measurement points

仿真结果表明，质量数值受弹性模态影响很大，并且随着所选频带越来越趋近于弹性模态，质量参数的误差就越大。图2给出了板的第一阶弹性模态振型，在该阶模态处Z方向振动幅值最大，Y方向和X方向幅值很小，而对于使用质量线原理识别惯性参数而言，要设法避免弹性模态影响，那么对于振动幅值较小的X和Y方向的数据，正是所期望的。从识别结果中发现，对于同一频率而言，X方向对应的质量数值精度最高，在Y方向结果次之，Z方向结果完全错误。

图4 使用DPPIM法识别不同方向上的质量数值Fig.4 Using the DPPIM method to identify the quality values in different directions

分别使用直接参数识别法直接计算10个参数，和将X方向质量值代入质量线法，继续计算其余9参数。两组结果的误差随选择频带的变化如图5所示。

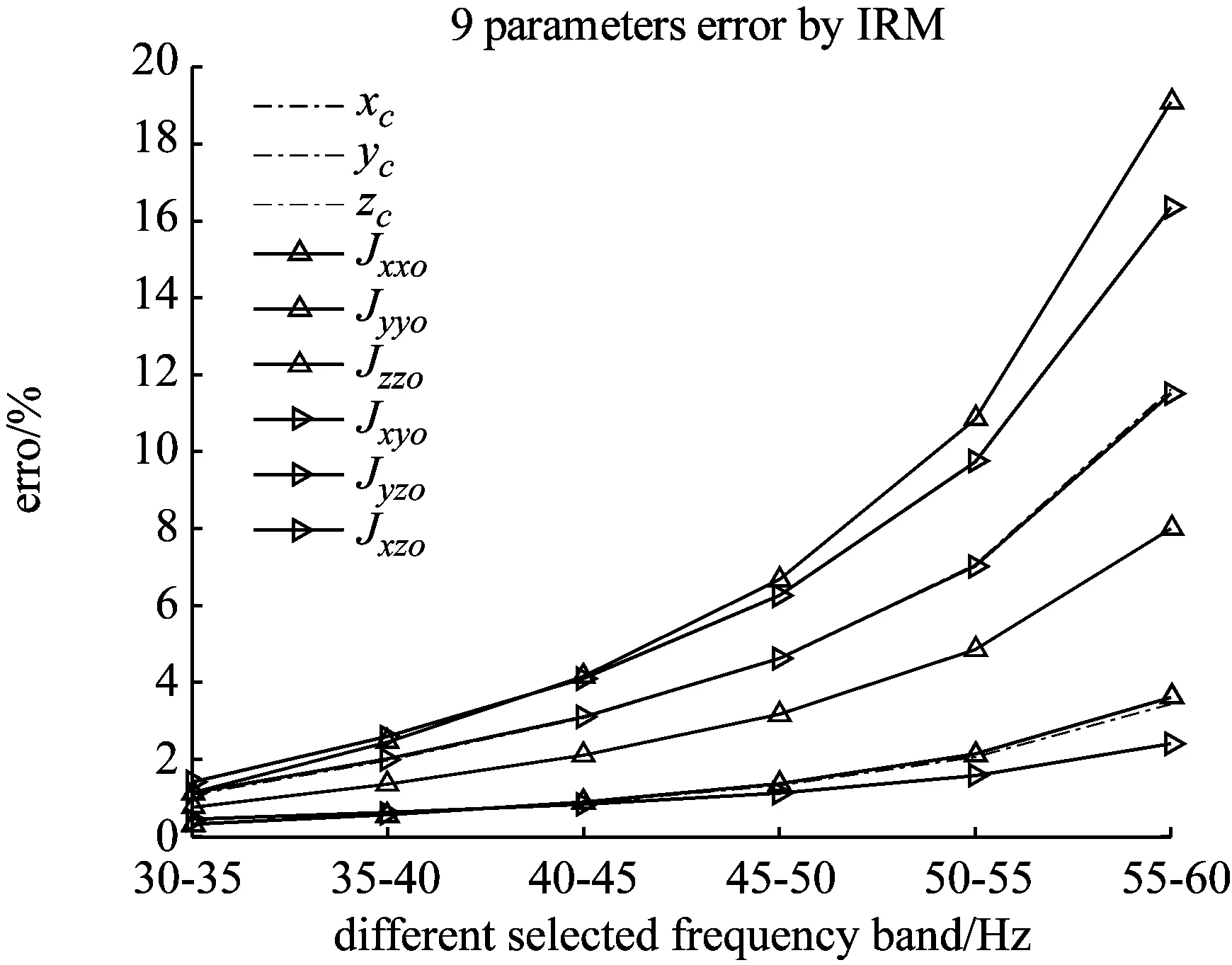
图5 DPPIM法和IRM法识别剩余9个参数的误差Fig.5 Identification error of the remaining 9 parameters by DPPIM method and IRM method

由图5可以看出，直接参数识别法的识别精度远远低于质量线法，含有弹性模态影响时，有时甚至完全错误。

2.2 响应点布置在弹性模态的节点处

图6表示响应点在弹性模态节点上频响函数，图7表示使用DPPIM法识别在不同方向上的质量数值。

图6 响应点在弹性模态节点上频响函数Fig.6 Frequency response functions of nodal points of the first mode

图7 使用DPPIM法识别在不同方向上的质量数值Fig.7 Mass values identified from diffreent directions by DPPIM method

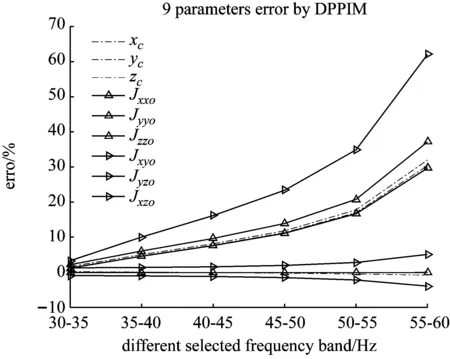
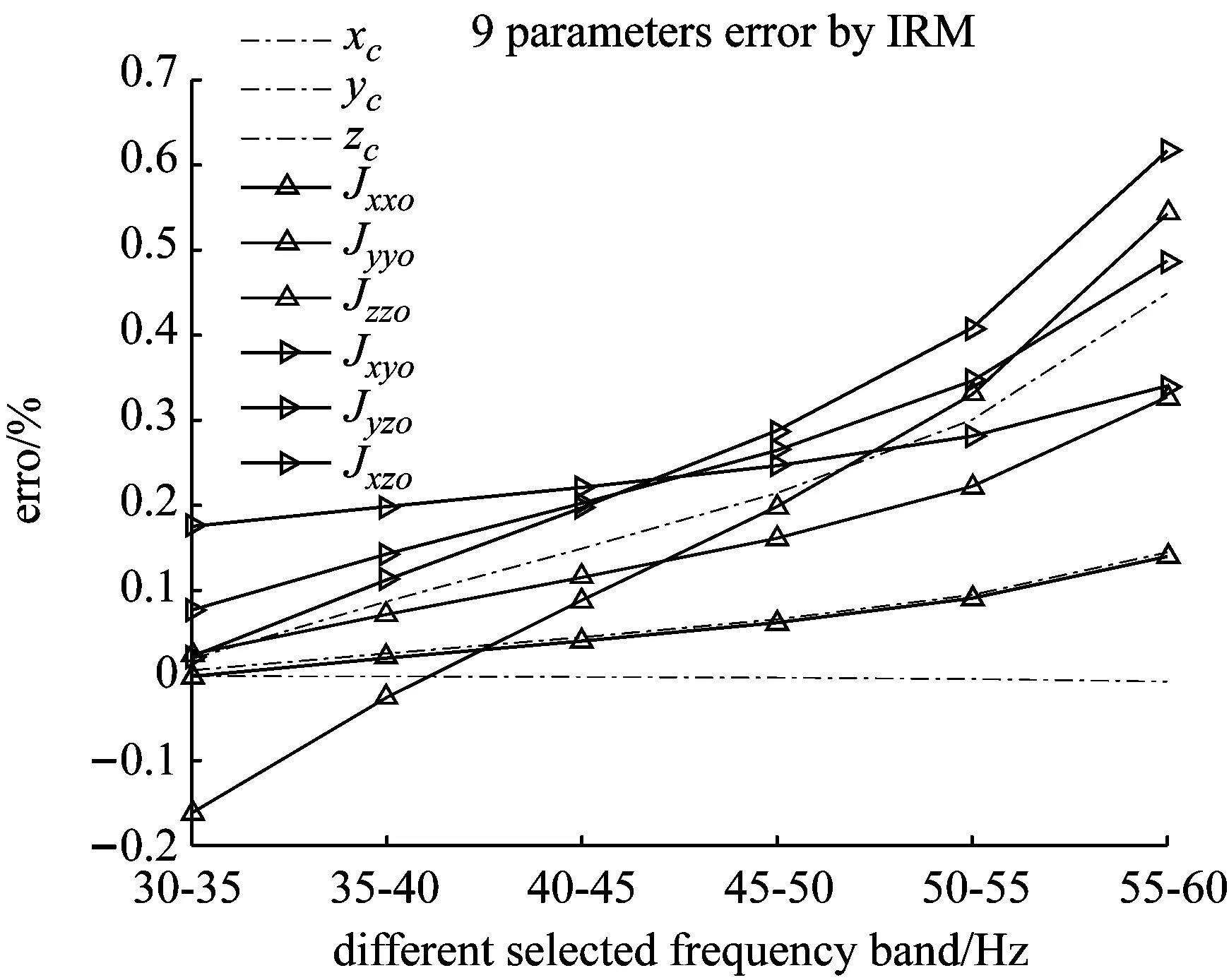
图8 DPPIM法和IRM法识别剩余9参数的误差Fig.8 Identification error of the remaining 9 parameters by DPPIM method and IRM method

图8为将响应点布置在弹性模态节点处的识别误差与所选频带的关系。可以看出，将响应点布置在弹性模态的节点上可有效减小频率响应函数弹性模态的幅值，从而减小弹性模态的影响，识别精度显著提高。

2.3 噪声对精度的影响

在频响函数中添加40%噪声(20%白噪声和20%有色噪声)，频响函数幅值如图9所示。重复计算50次，误差平均值、误差方差、误差最大值和最小值如表2和表3所示。

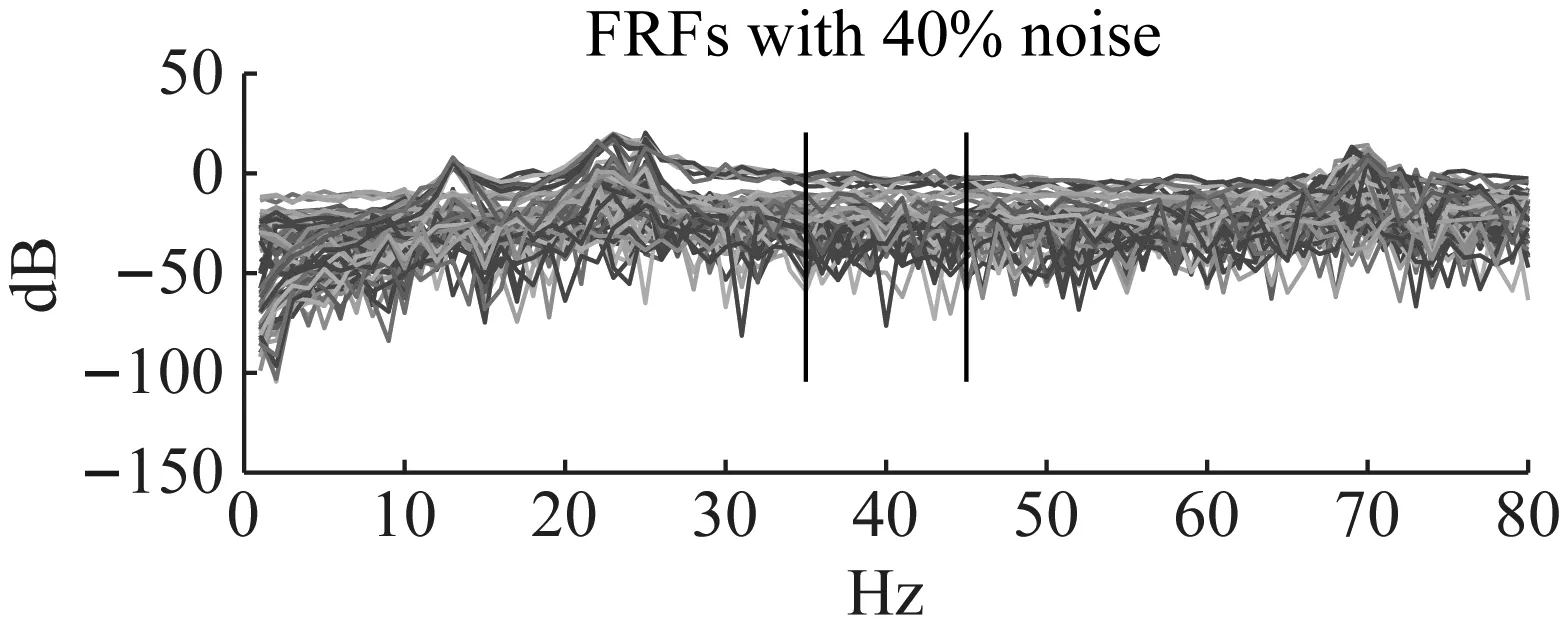
图9 40%噪声的频响函数Fig.9 Frequency response functions with 40% noise

表2 DPPIM法各参数最大误差(50次)
Tab.2The maximum error of each parameter inDPPIM method(50 times)

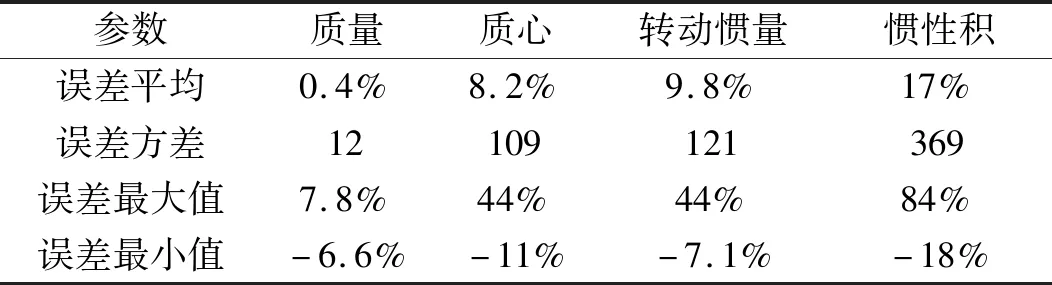
参数质量质心转动惯量惯性积误差平均0.4%8.2%9.8%17%误差方差12109121369误差最大值7.8%44%44%84%误差最小值-6.6%-11%-7.1%-18%

表3 IRM法各参数最大误差(50次)Tab.3 The maximum error of each parameter in IRM method(50 times)

仿真结果表明：与直接参数识别法相比，质量线法具有更高的可靠性，在较大噪声输入的情况下，直接参数识别法精度迅速下降，而质量线法依然保持了很高的精度。

3 实验验证

以某型列车转向架构架为实验对象，在环境噪声影响较大的工厂厂区内验证本文的结论。构架结构如图10所示。

由于感兴趣的频响函数频率很低，因此需要选择较软的力锤锤头[13]。实验所选力锤型号为PCB 086C20，实测灵敏度为0.118 mV/N，三轴加速度传感器型号为PCB U356A08，数据采集设备为OROS-OR35，模态分析软件为N-Modal。进行本改进方法测试之前需要先测试出弹性模态频率与振型，然后降低采样频率，使分析频率仅稍高于第一阶弹性模态频率，并提高频率分辨率，以进行本改进方法实验。测点分布、第一阶弹性振型和测试自由度布置分别如图11～图13所示。

图10 构架全貌Fig.10 The frame of a bogie

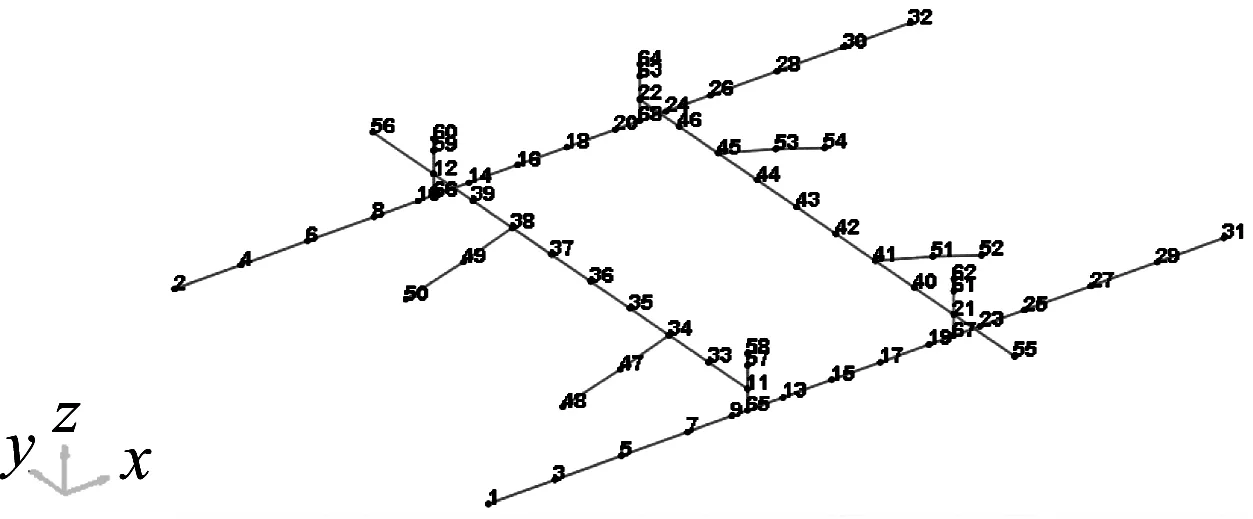
图11 测试弹性模态所布置的测点Fig.11 Measurement points in the elastic modal test

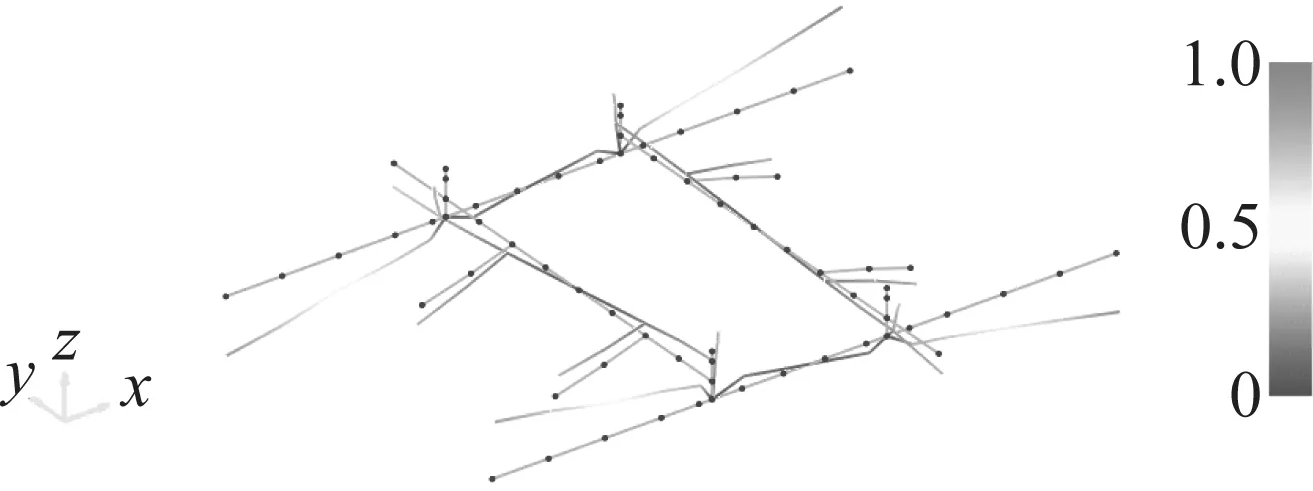
图12 第一阶弹性模态振型Fig.12 First elastic mode

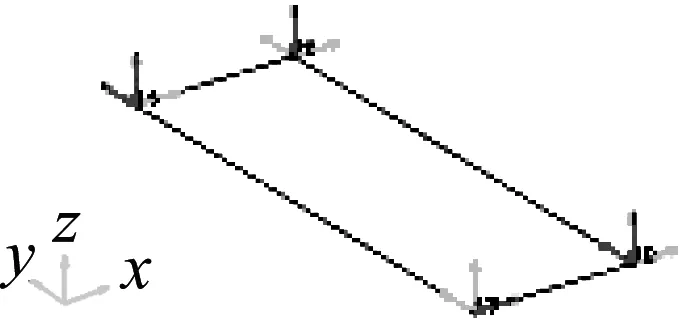
图13 测试几何模型及测试自由度Fig.13 The geometry model and the test degree of freedoms

测点分布原则是反映刚体的几何轮廓，均匀分布，且测点要避开对称轴或转动节线，激振力方向不能全部平行，也不能通过质心，否则坐标转换矩阵条件数会变大，最小二乘法的结果将变得不稳定[14-15]。实验中，采样频率是128 Hz，频率分辨率为0.062 5 Hz，共800条谱线，八次锤击平均。部分相干函数和频响函数幅值如图14所示。

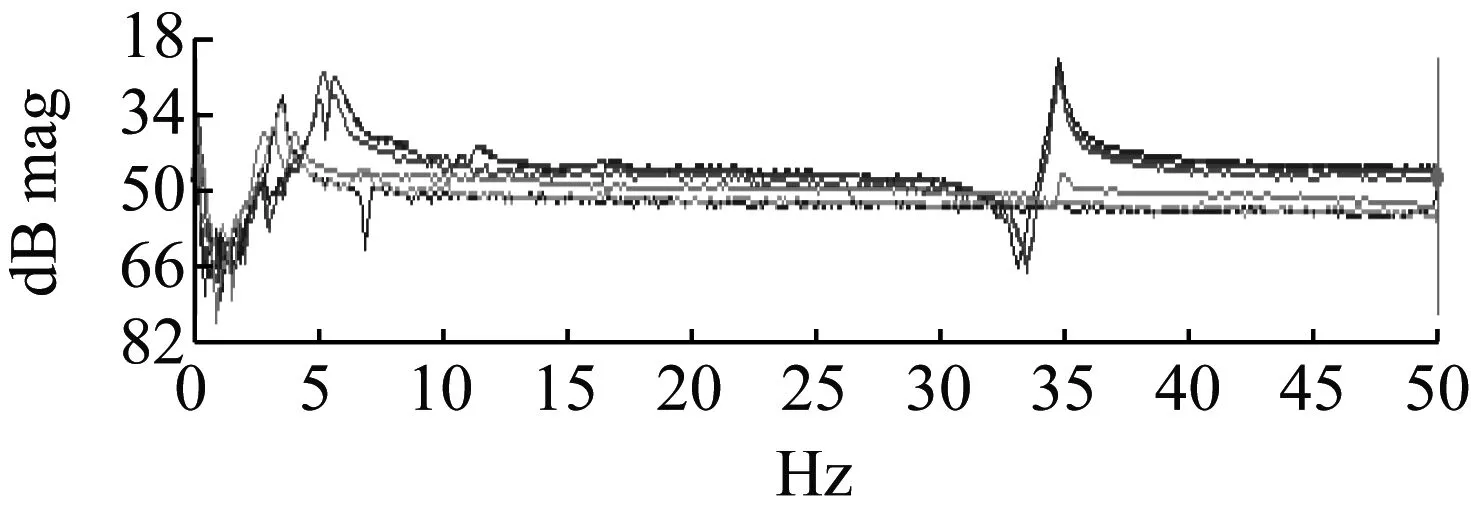
图14 部分测点的相干函数和频响函数Fig.14 The coherence and frequency response functions of some measurement points

选择一段谱线相对平直频带，使用直接参数识别法，求出X方向对应质量(X方向弹性模态幅值最小)在1 077～1 145 kg内波动，由称重法得到结构质量为1 097 kg，误差为-2%～4%，将识别得到的质量数值(1 077 kg和1 145 kg)代入质量线法中继续计算，得到剩余全部参数，如表4和表5所示。

表4 改进方法惯性参数识别结果(m=1 077 kg)Tab.4 Inertia parameter identification results of the improved method(m=1 077 kg)

表5 改进方法惯性参数识别结果(m=1 145 kg)Tab.5 Inertia parameter identification results of the improved method(m=1 045 kg)

惯性主轴的方向是几乎平行于坐标轴，与实际结构的对称性一致。与厂家给出的惯性参数参考值(表6)相比，质量误差不超过±5%，主转动惯量误差不超过10%，质心误差不超过±1%，符合工程实践要求。

表6 厂家提供的惯性参数参考值(m=1 097 kg)Tab.6 Reference value of inertial parameters provided by the manufacturer(m=1 097 kg)

4 结 论

结合仿真结果和实际实验情况，提出一种先通过直接参数识别法识别质量，再使用质量线法识别其他参数的改进方法。其具有精度高，可操作性强，不依赖其他条件或操作的优点，通过仿真和实际实验验证了本改进方法的适用性，具有一定的工程实践意义。