基于相对加速度-相对速度控制的半主动惯容隔振器动态特性研究

王 勇，汪若尘，孟浩东，张步云

(1.江苏大学 汽车工程研究院，江苏 镇江 212013；2.上海大学 上海市应用数学和力学研究所，上海 200072；3.常州工学院 机械与车辆工程学院，江苏 常州 213002)

惯容器的结构实现形式主要有齿轮齿条式[8]、滚珠丝杠式[9]以及液力式[10-11]等，当惯容器的惯质系数为定值且不能调节时，此惯容器为被动惯容器。Chen等[12]首次提出了“半主动惯容器”的概念，半主动惯容器的惯质系数不是一个定值，在工作过程中能够进行调节，半主动惯容隔振器可以通过在滚珠丝杠式惯容器中安装可控惯性飞轮[13]或调节液力式惯容器中的管径[14]来实现。作为一种新型的结构装置，半主动惯容器已经运用于汽车悬架[15]与动力吸振器[16]中，研究表明采用半主动惯容器后，这些装置具有更好的减振性能。

目前鲜有关于半主动惯容隔振器的研究，本文将半主动惯容器应用到隔振器中，根据惯容器的力学特性，提出相对加速度-相对速度控制策略来调节半主动惯容器的惯质系数在最大与最小惯质系数间切换，详细分析此控制策略的有效性，其逻辑意义与半主动减振器中调节阻尼的相对速度-相对位移控制策略[17]类似。本文研究最基本的三元件并联式与串联式半主动惯容隔振器在基础简谐激励下的动态特性，其中惯容、弹簧和阻尼的元件个数各为1个，分别为单自由度与1.5自由度系统，运用平均法求解半主动惯容隔振器的动态响应，定义动态位移峰值、绝对位移传递率峰值、隔振频带以及高频带的绝对位移传递率四个评价指标[18]来评价半主动惯容隔振器的隔振性能，并与被动惯容隔振器进行对比分析。

1 并联式半主动惯容隔振器

并联式半主动惯容隔振器如图1所示，其中惯容器、弹簧与阻尼器处于并联状态。半主动惯容器的可控惯质系数为b；弹簧刚度为k；阻尼器的阻尼系数为c；x为承载质量m从静态平衡位置开始时的位移；外界激励为基础简谐激励y=ymcos(ωt)。

并联式半主动惯容隔振器在基础简谐激励下的动力学方程为

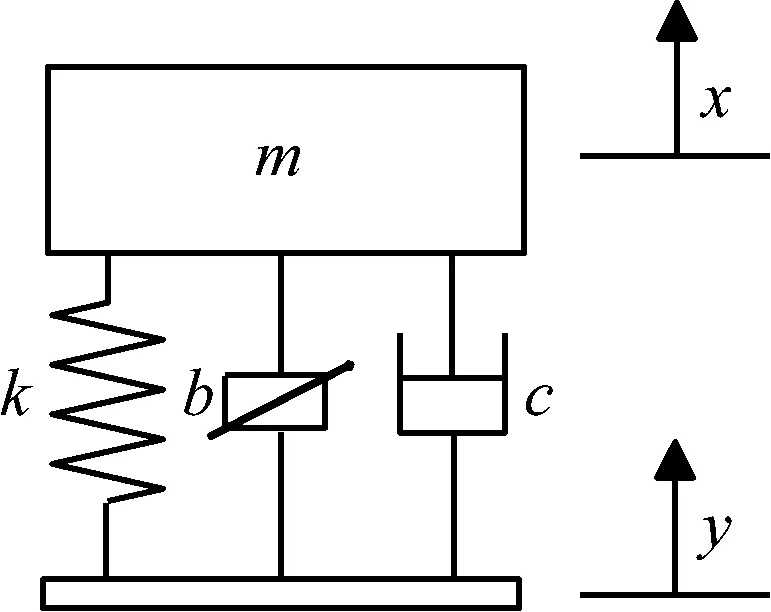
图1 并联式半主动惯容隔振器Fig.1 Parallel-connection semi-active inerter-based vibration isolator

(1)

本文为简化分析，考虑半主动惯容器在调节惯质系数时是实时快速地调节，不考虑其调节响应时间，根据相对加速度-相对速度控制策略，半主动惯容器的可控惯质系数调节规律如下

(2)

式中,bmax，bmin分别为可调节的最大与最小惯质系数。

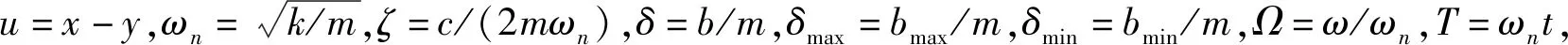
u″+δu″+2ζu′+u=Ω2ymcos(ΩT)

(3)

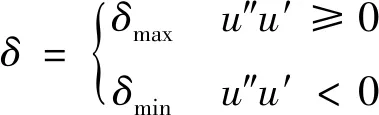
(4)

式(3)与式(4)表示对参数T求导。从式(3)与式(4)可看出，并联式半主动惯容隔振器是单自由度分段系统，对于分段系统，采用平均法可以很方便地求得系统的动态响应[19]，因此运用平均法求解式(3)的近似解析解，假设系统相对位移u的解的形式为

u=umcosφu

(5a)

u′=-umΩsinφu

(5b)

式中,φu=ΩT+θu，分别将式(5a)与(5b)对参数T进行求导，可得

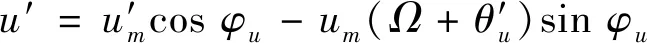
(6a)

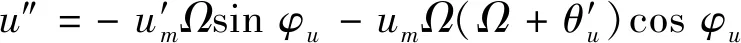
(6b)

将式(6a)与式(5b)结合，式(6b)与式(3)结合，可得

(7a)

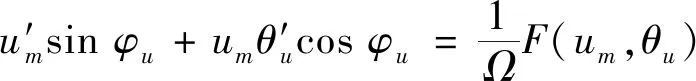
(7b)

F(um,θu)=(1-Ω2)umcosφu-δumΩ2cosφu-

2ζΩumsinφu-Ω2ymcos(φu-θu)

(7c)

由式(7a)与(7b)可得

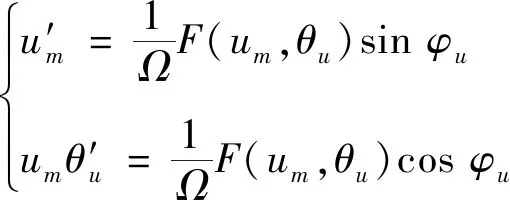
(8)

根据平均法的思想，将式(8)在一个周期内平均化可得近似解析解的振幅和相位的显示表达式

(9)

将式(5a)代入到式(4)中，可得惯质比δ在一个周期内的变化规律

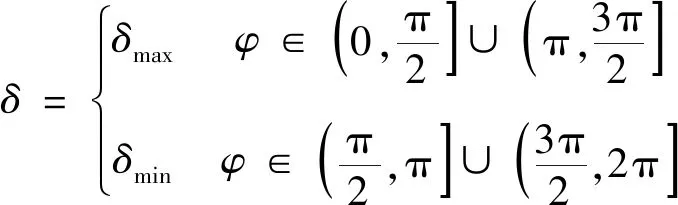
(10)

结合式(10)，对式(9)进行积分计算，可得

πΩ2ymsinθu]

(11a)

(11b)

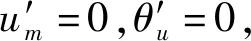
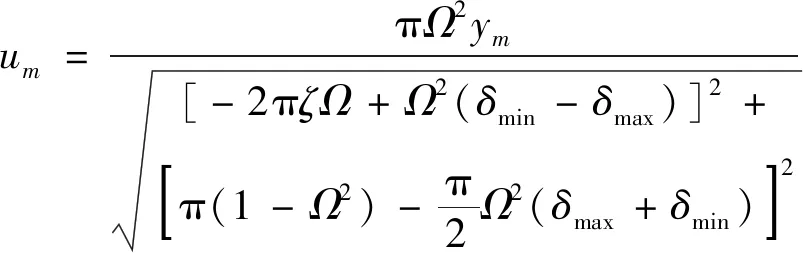
(12a)

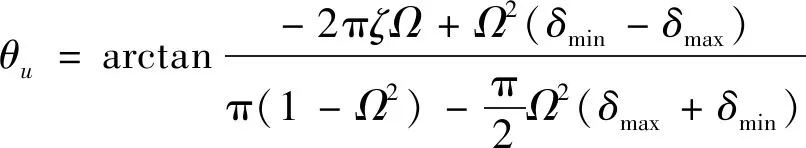
(12b)

依据x=u+y，可得系统绝对位移振幅和相位

x=xmcos(ΩT+γ)

(13a)

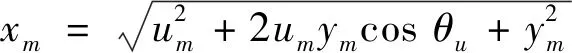
(13b)

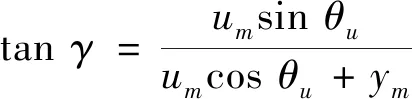
(13c)

将式(12a)与式(12b)代入到式(13b)中，可得系统绝对位移的稳态振幅

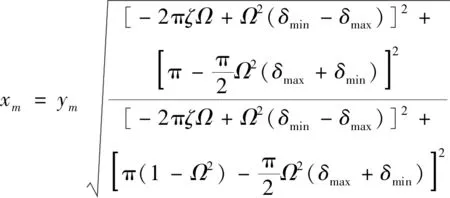
(14)

依据式(14)，可得并联式半主动惯容隔振器的绝对位移传递率

(15a)

(15b)

隔振器的隔振性能用动态位移峰值，绝对位移传递率峰值，隔振频带以及高频带的绝对位移传递率四个性能评价指标来评价，其中本文中的高频带的绝对位移传递率取激励频率趋于无穷时的绝对位移传递率。动态位移峰值决定了隔振物体在振动过程中的最大位移，绝对位移传递率峰值决定了传递到隔振物体的最大传递率，在实际工程中这两个数值不应太大；隔振频带表明在此频带内，绝对位移传递率小于1，隔振器有隔振效果；高频带的绝对位移传递率反映了隔振器在高频带的隔振性能。分别将式(12a)，式(14)与式(15b)对激励频率进行求导，利用数值求解可确定相对位移峰值、绝对位移峰值与绝对位移传递率峰值，以及其所对应的激励频率，后两个性能评价指标如下

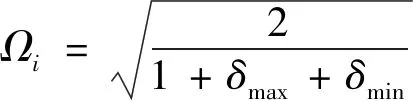
(16a)

(16b)

并联式半主动惯容隔振器的隔振性能需与并联式被动惯容隔振器及线性隔振器进行比较。基础简谐激励下并联式被动惯容隔振器与线性被动隔振器的相对位移振幅、绝对位移振幅及绝对位移传递率为

并联式被动惯容隔振器

(17a)

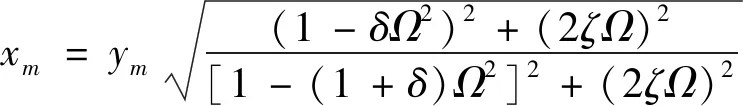
(17b)

(17c)

线性被动隔振器

(18a)

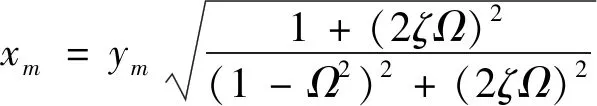
(18b)

(18c)

依据式(17)与式(18)，可确定四个性能评价指标

并联式被动惯容隔振器

(19)

线性被动隔振器

(20)

当最小惯质比δmin与最大惯质比δmax取不同值时，并联式半主动惯容隔振器相对位移、绝对位移与绝对位移传递率如图2和图3所示，并与并联式被动惯容隔振器及线性被动隔振器进行对比分析，图中的相对位移峰值、绝对位移峰值与绝对位移传递率峰值用圆圈表示。本文中系统阻尼比ζ=0.1，基础简谐激励幅值ym=0.02m。当惯质比δ增加时，并联式被动惯容隔振器的相对位移峰值、绝对位移峰值与绝对位移传递率峰值都逐渐减小，隔振频带逐渐变宽，高频带的绝对位移传递率逐渐增大；与线性被动隔振器相比，其高频带的隔振性能较差。

从图2与图3中可看出，当δmax为定值而δmin变化时，随着δmin的增加，并联式半主动惯容隔振器的相对位移峰值、绝对位移峰值与绝对位移传递率峰值逐渐增大，隔振频带逐渐变宽，高频带的绝对位移传递率逐渐增大；当δmin为定值而δmax变化时，随着δmax的增加，并联式半主动惯容隔振器的相对位移峰值、绝对位移峰值与绝对位移传递率峰值逐渐减小，隔振频带逐渐变宽，高频带的绝对位移传递率逐渐增大；与并联式被动惯容隔振器相比，其相对位移峰值、绝对位移峰值与绝对位移传递率峰值较小，隔振频带与高频带的绝对位移传递率介于δ=δmin与δ=δmax之间。

(a)相对位移

(c)绝对位移传递率

(a)相对位移

(b)绝对位移

此时需验证运用平均法求解解析解的精确性，并联式半主动惯容隔振器相对位移解析解与数值解对比如图4所示。数值解通过结合式(4)，并运用四阶定步长的龙格库塔法对式(3)进行数值积分得到，从图中可看出，解析解与数值解比较一致，验证了解析解的精确性与可靠性，表明运用平均法求解并联式半主动惯容隔振器的动态响应是可行的。

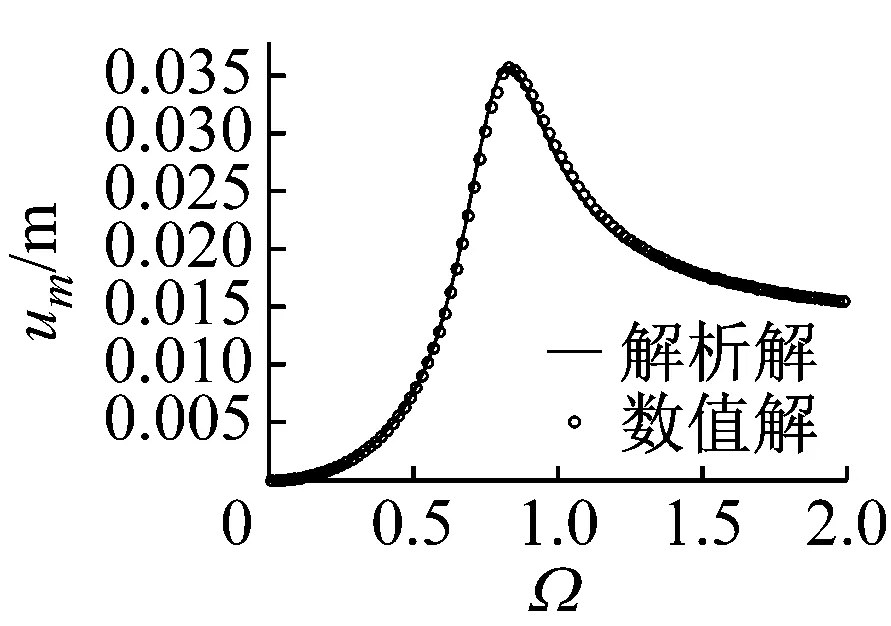
(a)δmax=1 δmin=0

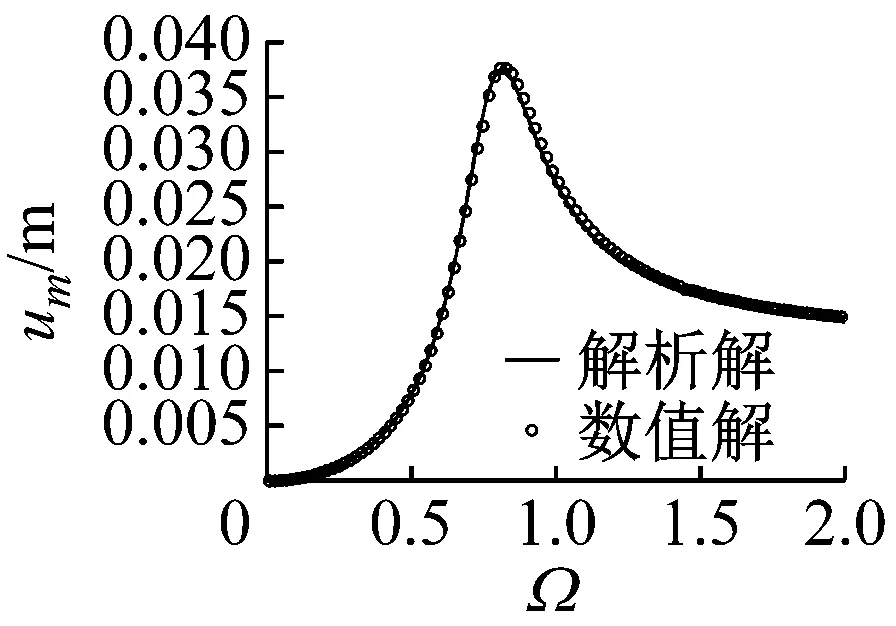
(b)δmax=1 δmin=0.1图4 并联式半主动惯容隔振器相对位移解析解与数值解对比Fig.4 Comparison between analytical results and numerical results of the relative displacement for the parallel-connection semi-active inerter-based vibration isolator

2 串联式半主动惯容隔振器

串联式半主动惯容隔振器如图5所示，其中惯容器与阻尼器先串联再与弹簧并联。

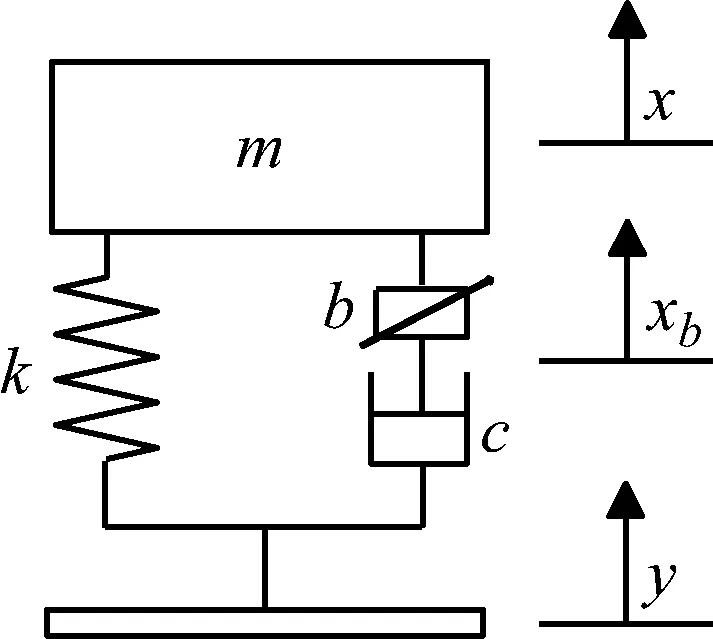
图5 串联式半主动惯容隔振器Fig.5 Series-connection semi-active inerter-based vibration isolator

串联式半主动惯容隔振器为1.5自由度分段系统，其在基础简谐激励下的动力学方程为

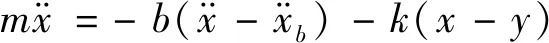
(21a)

(21b)

令u=x-y，v=xb-y，与并联式半主动惯容隔振器类似，式(21)可化简为

u″+δu″-δv″+u=Ω2ymcos(ΩT)

(22a)

-δu″+δv″+2ζv′=0

(22b)

为方便运用平均法求解系统的动态响应，将式(22a)与式(22b)分别化简为只包含u″与v″的动力学方程，如下

u″+2ζv′+u=Ω2ymcos(ΩT)

(23a)

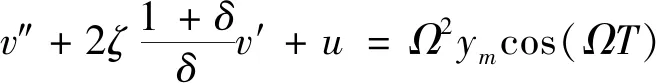
(23b)

系统相对位移u的解的形式如式(5)所示，相对位移v的解的形式为

v=vmcosφv

(24a)

v′=-vmΩsinφv

(24b)

式中,φv=ΩT+θv，分别将式(24a)与(24b)对参数T进行求导，可得

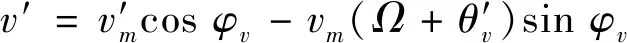
(25a)

(25b)

将式(25a)与式(24b)结合，可得

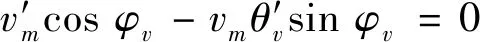
(26)

将式(5)，式(6)，式(24)，式(25)代入式(23)中，可得

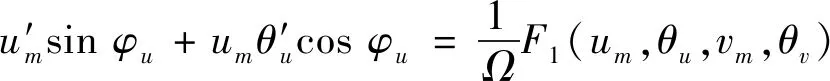
(27a)

F1(um,θu,vm,θv)=um(1-Ω2)cosφu-

2ζΩvmsinφucos(θu-θv)+2ζΩvmcosφusin(θu-θv)-

Ω2ymcosφucosθu-Ω2ymsinφusinθu

(27b)

(27c)

F2(um,θu,vm,θv)=-vmΩ2cosφv+

umcosφvcos(θv-θu)+umsinφvsin(θv-θu)-

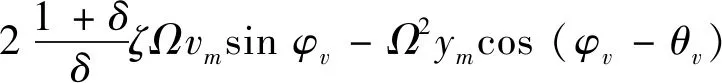
(27d)

由式(27a)与(7a)，式(27c)与式(26)可得

(28)

运用式(10)，将式(28)在一个周期内平均化可得近似解析解的振幅和相位的显示表达式

πΩ2ymsinθu]

(29a)

πΩ2ymcosθu]

(29b)

πumsin(θv-θu)-πΩ2ymsinθv+

(29c)

(29d)

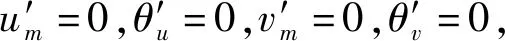
-2ζΩvmcos(θu-θv)=Ω2ymsinθu

(30a)

um(1-Ω2)+2ζΩvmsin(θu-θv)=Ω2ymcosθu

(30b)

(30c)

-πvmΩ2+πumcos(θv-θu)+

(30d)

运用非线性代数方程组求解方法求解此四元非线性方程组，可得串联式半主动惯容隔振器相对位移的稳态振幅和相位，绝对位移与绝对位移传递率可通过式(13b)与式(15a)求得。串联式半主动惯容隔振器的四个评价指标确定过程如下。

(1)相对位移峰值ump

将式(30)对激励频率求导，可得

(31a)

(31b)

2πΩymsinθv

(31c)

2πΩymcosθv

(31d)

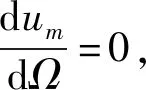
(2)绝对位移峰值xmp，绝对位移传递率峰值Tap

运用式(13b)，对于绝对位移峰值xmp，有

(32)

结合式(31)，式(32)与相位θu及θv的三角函数公式，求解此非线性方程组，可确定绝对位移峰值xmp，绝对位移传递率峰值Tap=xap/ym。

(3)隔振频带

运用式(15a)，在隔振频率Ωi处，有

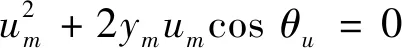
(33)

结合式(30)与式(33)，求解此非线性方程组，可确定隔振频带。

(4)高频带的绝对位移传递率Talim

对于串联式半主动惯容隔振器，有

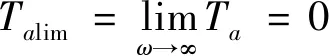
(34)

基础简谐激励下串联式被动惯容隔振器的相对位移振幅、绝对位移振幅及绝对位移传递率为

(35a)

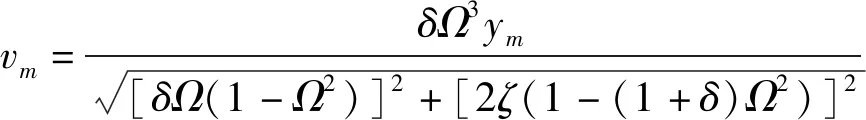
(35b)

(35c)

(35d)

与并联式被动惯容隔振器不同，串联式被动惯容隔振器的相对位移峰值、绝对位移峰值与绝对位移传递率峰值难以用一个解析表达式来表示，但仍可以先通过将式(35)对激励频率进行求导再运用数值法求解得到，所以这里不再详细论述其求解过程，后两个性能评价指标如下

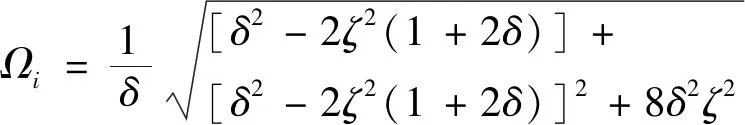
(36a)

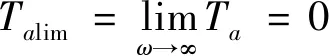
(36b)

当惯质比δ取不同值时，串联式被动惯容隔振器相对位移峰值、绝对位移峰值、绝对位移传递率峰值与隔振频带如图6所示，并与线性被动隔振器进行对比分析。当惯质比δ增加时，串联式被动惯容隔振器的相对位移峰值、绝对位移峰值与绝对位移传递率峰值逐渐减小，隔振频带先变宽后变窄。与线性被动隔振器相比，串联式被动惯容隔振器的隔振频带较宽，高频带的绝对位移传递率都趋于0，当惯质比δ取值较大时，其相对位移峰值、绝对位移峰值与绝对位移传递率峰值较小，反之较大。

当最小惯质比δmin与最大惯质比δmax取不同值时，串联式半主动惯容隔振器相对位移、绝对位移与绝对位移传递率如图7及图8所示。当δmax为定值而δmin变化时，随着δmin的增加，串联式半主动惯容隔振器的相对位移峰值、绝对位移峰值与绝对位移传递率峰值先减小后增大，隔振频带逐渐变窄；当δmin为定值而δmax变化时，随着δmax的增加，串联式半主动惯容隔振器的相对位移峰值、绝对位移峰值与绝对位移传递率峰值逐渐减小，隔振频带逐渐变窄；与串联式被动惯容隔振器相比，其隔振频带介于δ=δmin与δ=δmax之间，高频带的绝对位移传递率都趋于0，当最小惯质比δmin与最大惯质比δmax取值较大时，相对位移峰值、绝对位移峰值与绝对位移传递率峰值较小，反之较大。

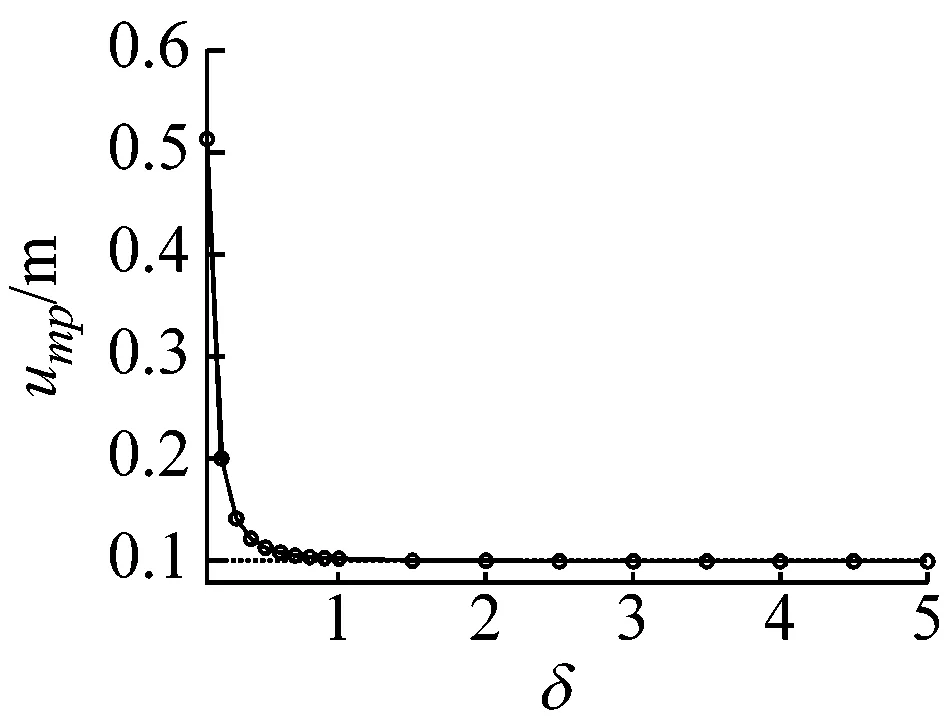
(a)相对位移峰值

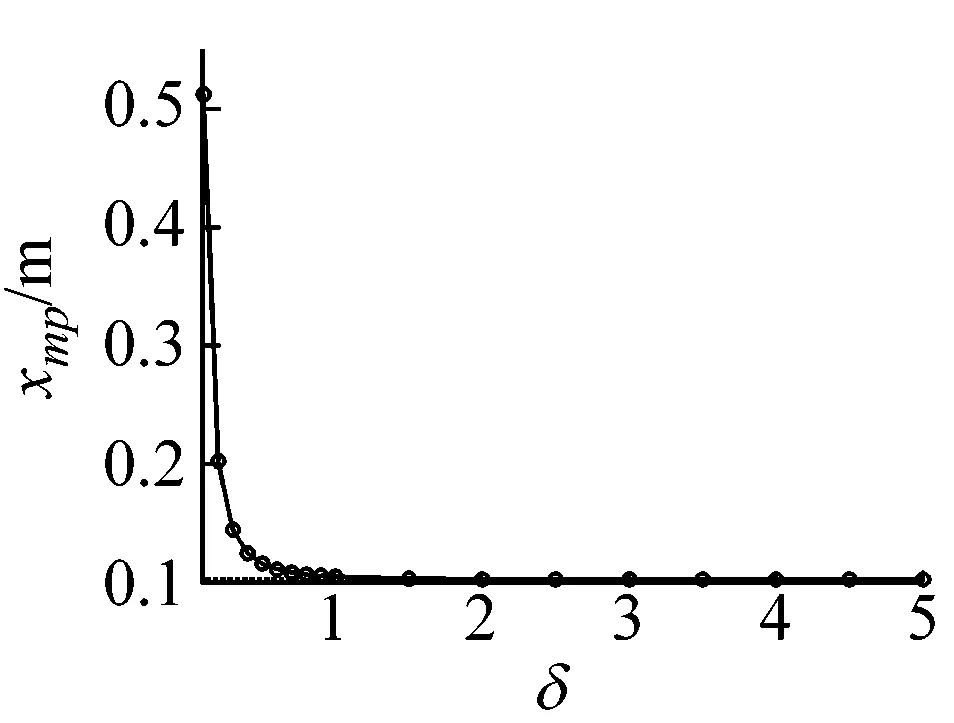
(b)绝对位移峰值

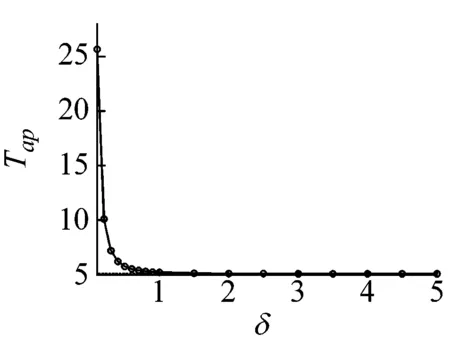
(c)绝对位移传递率峰值

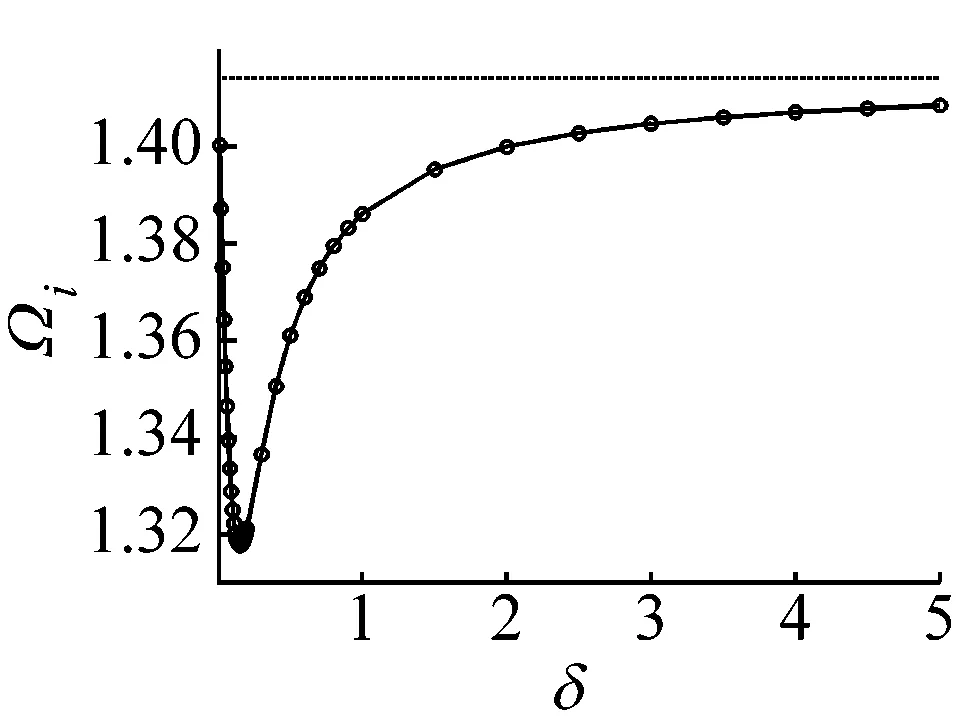
(d)隔振频带图6 δ取不同值时，串联式被动惯容隔振器四个性能评价指标Fig.6 Four performance indexes of the series-connection passive inerter-based vibration isolator with different δ

(a)相对位移

(b)绝对位移

(c)绝对位移传递率

(a)相对位移

(b)绝对位移

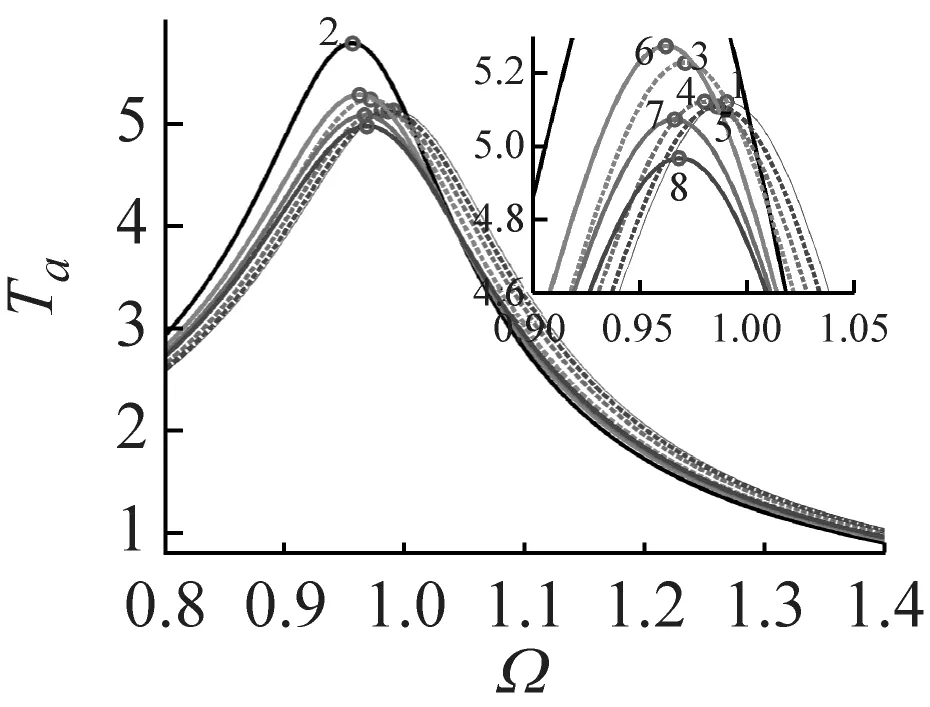
(c)绝对位移传递率

串联式半主动惯容隔振器相对位移解析解与数值解对比如图9所示，数值解通过结合式(4)，并运用四阶定步长的龙格库塔法对式(23)进行数值积分得到。从图中可看出，对于相对位移u，在峰值频带附近，解析解相较数值解误差较大，而在其他频带内，解析解与数值解误差较小；对于相对位移v，在整个频带内，解析解与数值解比较一致，验证了解析解的精确性与可靠性，表明运用平均法求解串联式半主动惯容隔振器的动态响应是可行的。

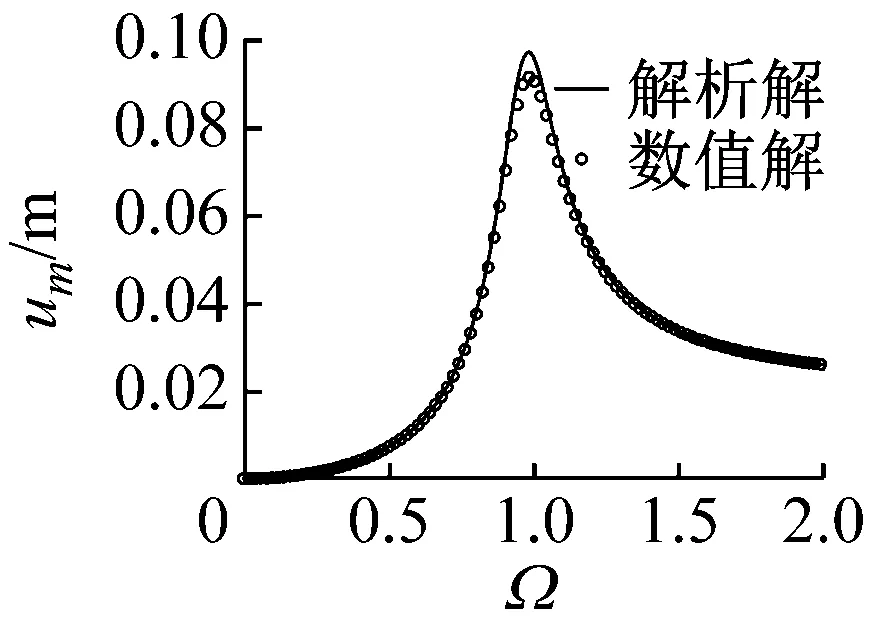
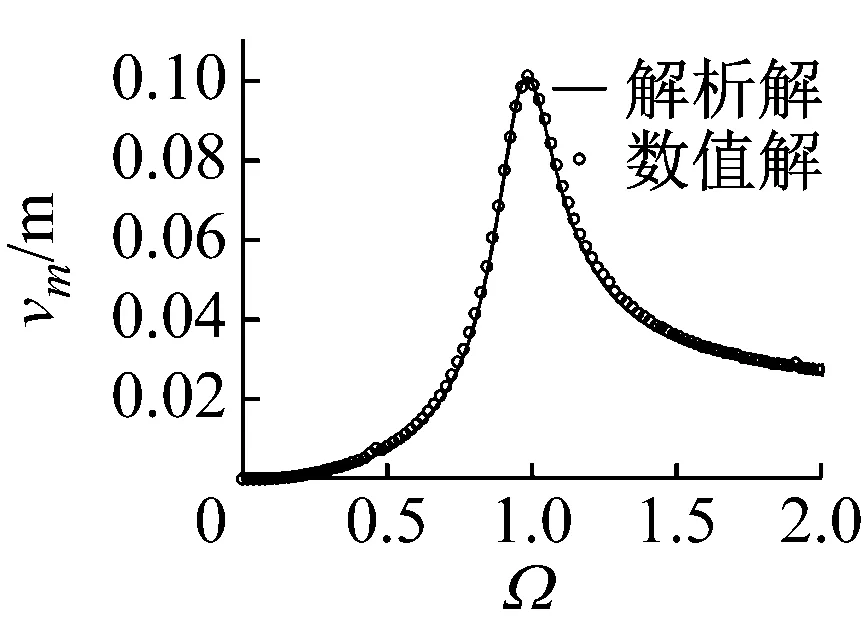
图9 串联式半主动惯容隔振器相对位移解析解与数值解对比(δmin=0.5，δmax=5)Fig.9 Comparison between analytical results and numerical results of the relative displacement for the series-connection semi-active inerter-based vibration isolator(δmin=0.5，δmax=5)

3 两种半主动惯容隔振器隔振性能对比分析

并联式与串联式半主动惯容隔振器隔振性能对比如图10所示，对比结果与相应的被动惯容隔振器比较结果类似。与串联式半主动惯容隔振器相比，并联式半主动惯容隔振器的相对位移峰值、绝对位移峰值与绝对位移传递率峰值较小，隔振频带较宽，但高频带的绝对位移传递率较大。

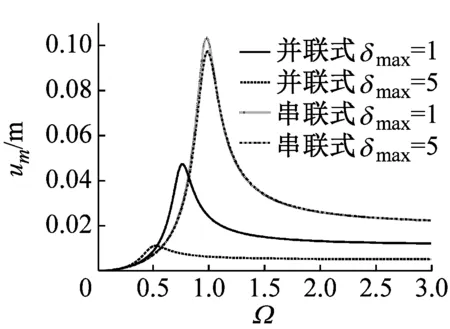
(a)相对位移

(b)绝对位移

(c)绝对位移传递率图10 两种半主动惯容隔振器隔振性能对比(δmin=0.5)Fig.10 Comparison of the isolation performance of the two semi-active inerter-based vibration isolators(δmin=0.5)

4 结 论

本文将半主动惯容器应用于隔振器中，提出了相对加速度-相对速度控制策略，研究了并联式与串联式半主动惯容隔振器在基础简谐激励下的动态特性，结果表明：

(1)运用平均法可以方便地求解半主动惯容隔振器的动态响应，且解析解与数值解比较一致，验证了解析解的精确性与可靠性。

(2)采用相对加速度-相对速度控制的并联式半主动惯容隔振器，相较并联式被动惯容隔振器，其相对位移峰值、绝对位移峰值与绝对位移传递率峰值较小，隔振频带与高频带的绝对位移传递率介于δ=δmin与δ=δmax之间。

(3)采用相对加速度-相对速度控制的串联式半主动惯容隔振器，相较串联式被动惯容隔振器，其隔振频带介于δ=δmin与δ=δmax之间，高频带的绝对位移传递率都趋于0，当最小惯质比δmin与最大惯质比δmax取值较大时，相对位移峰值、绝对位移峰值与绝对位移传递率峰值较小。

(4)相较串联式半主动惯容隔振器，并联式半主动惯容隔振器的相对位移峰值、绝对位移峰值与绝对位移传递率峰值较小，隔振频带较宽，但高频带的绝对位移传递率较大。