多段式拖曳系统随机振动传递隔振模拟

王志博

(江苏科技大学 船舶与建筑工程学院,江苏 张家港 215600)

拖曳系统航行于复杂多变的海况环境下，由单段缆与单个拖曳体或线列阵形成。母船受到风浪流的作用时拖曳系统处于高刚度低阻尼状态，在连接绞车的吊点处形成的随机振动沿着拖曳缆传递，使得拖曳系统发生同样的随机振动,由于单段缆处于高张力状态，缆的阻尼极低，缆受到涡激励振动等振动激励，这些扰动的传递几乎无衰减，故对这种结构的控制或补偿措施，往往无法取得有效的控制效果。Pang等[1-3]等运用二段式设计的思想来减低缆内张力，沉降拖曳体，二段式或者多段式的拖曳系统的设计思想是，通过改变缆内张力，使缆处于松弛状态，那么缆的结构阻尼和水动力阻尼显著增强，对扰动的传递的衰减作用将十分显著。模拟拖曳系统的方法主要有凝集参数法、有限元方法、有限体积法，Wang等[4]应用有限元方法模拟了二段式拖曳系统的隔振效果，同样Schram等[5]模拟了空气中拖曳系统的运动特征，Wang等[6-7]模拟了拖曳系统的水面操纵的激励运动响应，随着缆内的结构阻尼的增强，对应的刻画缆内的阻尼的动力学模型的精确程度的要求也越高，当前各种拖曳缆受力分析建模的动力学方法对缆的结构阻尼和水动力阻尼的刻画程度各不相同，对于不考虑拖曳缆的结构阻尼的建模，预报低张力缆的振动传递，Zhu等[8]运用凝集参数方法模拟了水面运动传递体现了强线性特征，Lee等[9]运用有限节点单元法模拟了拖曳系统的运动，但缺乏对拖曳系统阻尼效应和拖曳体运动的描述模型，相比而言Park等[10]结合拖曳体运动模型求解拖曳系统的运动响应，相比有限元方法，有限体积法准确的耦合了结构阻尼效应，基于Ablow模型[11]，Gobat等[12]增加了拖曳缆的弯曲和扭转求解模型，但是求解不稳定程度却大大增加。Yoerger等[13]应用有限体积法格式分析了重型拖曳缆大缆长直航稳态拖曳形成的阻力和流动激励振动，发现缆受到的激励集中在低频段。Zhu等[14]着重模拟了圆形截面缆受到的涡激励震荡形成的冲击张力效应。Merz等[15]建立了描述缆的分段设计的动力学模型用于水下带缆的UUV设计。吴水源等[16]对多点提升系统中钢丝绳变形失谐现象进行了模拟分析，从振动传递的能谱分析失谐效应。于丹竹等[17]采用了降阶处理的水下隔振模型并进行仿真与验证。

本研究利用波谱密度函数生成扰动源，将扰动施加在拖曳缆的绞车端，对单段式拖曳、两段式拖曳以及多段式拖曳系统的运动响应进行计算分析，基于Huang[18]的算例进行验证。结合谱密度函数特征分析随机扰动传递的规律，着重考查不同幅度和频率的扰动传递受到隔振系统的阻尼效果。

1 随机振动传递计算模型

1.1 随机振动传递的动力学模型

多段式拖曳系统的结构如图1所示，按照凝集参数方法的基本思想，将多段式拖曳缆分成若干连续的段，可将缆段受到的分布力“集中”到节点上，如果缆段足够多，那么对缆的运动和受力的描述也足够的准确。当缆长足够长，可将缆看做均质受力响应沿着缆不变的柔性缆，不考虑缆扭转和弯曲造成的作用力，利用牛顿第二定律对节点进行运动和受力分析。如图2所示，在全局坐标系O-ijk中，将缆离散为N-1段，那么缆共有N个节点，任意节点n处的力有张力T，重力G、浮力B、附加质量力E、水流阻力D，若有其它悬挂物还要考虑额外作用力S，为便于计算机程序设计，在i,j,k方向分别写成矩阵形式为

M1×NAN×N=F1×N

(1)

在i,j,k方向分别有

式中：Ln和Ln-1是节点n相邻两缆段的缆长，ma是缆的附加质量系数，而ρ0是缆的线密度。

利用缆的运动速度描述对角矩阵An,n在i、j、k方向分别满足

任意节点n处的受力写成

F1,n=Tn+Gn+Bn+Dn+En+Sn

以下就受到的各种作用力分别建模，缆段在空间的相对位置是由节点坐标进行描述。式(2)为缆段n在t时刻的缆长

(2)

式(3)为在缆段之间采用线弹性关系近似缆的张拉状态

(3)

式(4)、式(5)为节点受到的重力与浮力

(4)

(5)

假设缆不受上升流作用，如图2所示水流作用力满足如下变换关系

其中,入流方向的分量(t,n,b)与全局坐标系(i,j,k)的坐标面O-ij的夹角为θ，投影与i轴的夹角为φ，入流速度幅值为C，节点运动速度矢量为

节点n与水流的相对速度

节点n受到的水流作用力为

(6)

其中Cx,Cy,Cz为缆段受到的水流阻力系数。

若节点n处缆悬挂了拖曳体，可将拖曳体看作质点，利用质点运动模型描述拖曳体的运动，根据牛顿第二定律将拖曳体简化成为质点运动写成

(7)

质量系数矩阵的非零元素为

Mb 1,1=m+max,

Mb 2,2=m+may,

Mb 3,3=m+maz，

其中,m为拖曳体的质量，max，may，maz为拖曳体的附加质量；XF，YF，ZF等为作用在拖曳体上的外力这些作用力仍为前述重浮力、惯性力，水流作用、拖曳缆拉力，需要利用来拖曳体的特征长度Lx,Ly,Lz计算水流作用力。

通常在水面端给定拖曳速度(U0,V0,W0)，属于第一类边界条件，本研究采用波浪谱生成的升沉运动的时间历程作为绞车端的运动边界。

(8)

式中,U0是指定的拖曳速度，W0是由Jonswap波谱生成的波高时序进行差分得到，由波高和波浪周期表示的谱公式，采用JONSWAP波谱扰动源的运动谱

(9)

生成的波谱与对应的速度时间序列如图3所示，缆端作为自由端时节点处受到的作用力最后一个缆段的水流阻力可利用式(3)计算，若缆末端连接拖曳体那么还需结合拖曳体的质量属性求解式(7)。在给定初始条件的前提下，可结合两个第一类边界条件。该模型按照矩阵向量形式进行描述，可结合MATLAB的常微分方程数值求解工具较为容易的求解方程组(1)，对于六自由度运动模型也可借助MATLAB相应的模型进行求解。在对定常缆型的计算中可将Δt看成控制迭代步长的控制器，通常可取自适应时间步长，在指定了求解误差后通常历经多次迭后即可收敛到一定的缆型，对非定常的缆型将时间步长取得足够小能够获得缆的运动响应。

图1 多段式拖曳系统的结构Fig.1 Structure of multi sections towed cable system

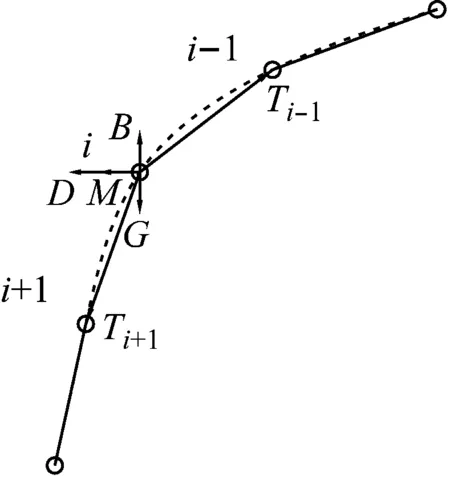
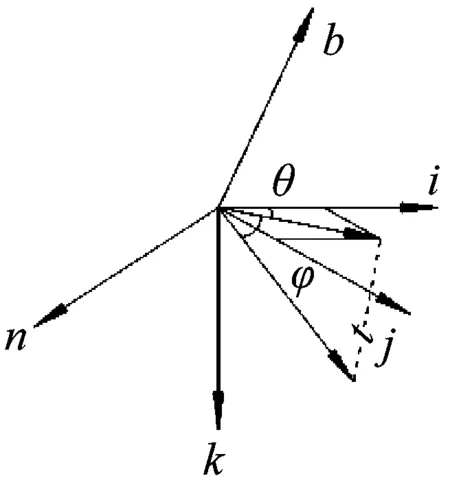
图2 缆结构与受力的参数凝集与坐标旋转转换Fig.2 Cable segments with lumped parameters and coordinates rotating transfer

1.2 动力学模型的计算验证

采用Huang(1994)模拟的拖曳系统回转运动算例来验证本研究的算例，并在尾端添加尾巴段，改变尾巴段的长度，在尾巴段端点处的拖曳体采用轻盈质量的小型拖曳体，拖曳系统的参数见表1。

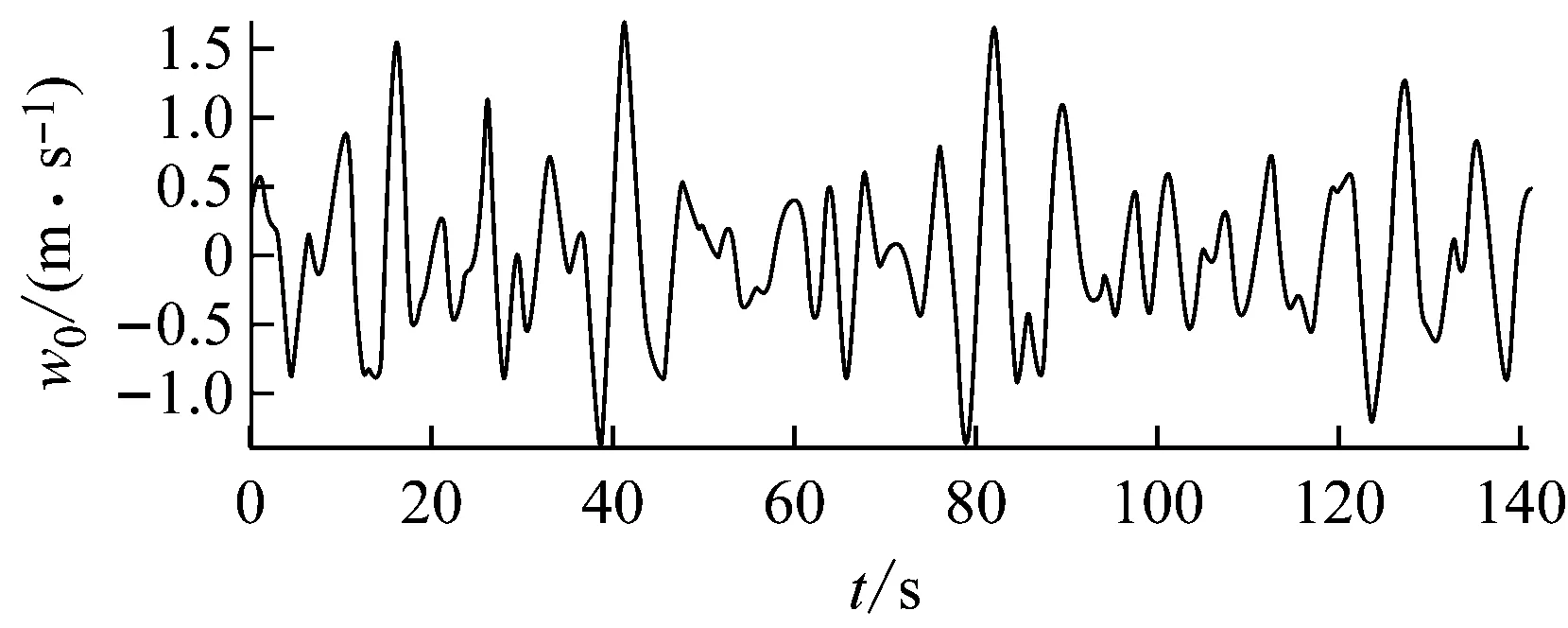
图3 波谱与对应的生成速度的时间序列Fig.3 Wave spectrum and its velocity sequence

表1 拖曳系统参数Tab.1 Towed cable system parameters

可见主拖缆的尾端拖曳体的重量较大而分枝缆的拖曳体质量较小但大缆长的分枝缆在小R/L回转运动情况下会出现跳跃的情况，在此拖曳系统中为了不改变回转运动的主要特征，为减小分枝缆内的张力作用，采用较小线密度的分枝缆和较小质量的末端拖曳体进行计算。图4显示了拖曳体以及带有一段拖曳缆全回转的运动的水平和升沉轨迹，验证了本模型的正确性。

2 多段式拖曳对振动传递的特性

2.1 二段拖曳系统的传递频谱特征

针对上述多段式的拖曳体的运动，展开扩展计算。由于原模型中的拖曳体的重量较大，拖曳体和主缆的重量比达到了1.85，可进一步降低主拖曳体的重量考查运动传递。

从图5中可以看出，拖曳系统的振动沿着多段式传递的基本规律，水面端的运动传递到拖曳体1时，运动形式几乎保持不变，但传递到拖曳体2时，升沉形式发生了很大的变化。呈现出微幅运动，慢速下潜的运动长周期响应，造成了“变频”效应。这是由于第二段缆长为200 m，拖曳体2对拖曳体1的升沉运动的响应近似于单摆运动，由于第二段缆是中性缆，近似水平姿态的的拖曳缆，受到了十分显著的水流阻尼力阻滞作用，由于缆的张紧和松弛交替作用，造成了拖曳体2的长周期的升沉，拖曳体2的微幅振动与拖曳体1的振动比较而言，还存在一定的滞后时差。图6显示了水面端和两个拖曳体振动的谱密度函数曲线，拖曳体1的升沉谱密度规律和水面端的基本一致，但是因第一段缆具有一定的阻尼耗散作用谱密度峰值有所降低，而拖曳体2的升沉运动谱密度仅仅只体现在长周期范围内。

图4 主拖曳体的水平面的运动轨迹和升沉轨迹的对比验证与扩展计算Fig.4 Comparison of main towed body horizontal paths and heave history and it extension

图5 拖曳体升沉的时间历程Fig.5 Heave history of each towed body

图6 升沉运动谱特征曲线Fig.6 The heaving motion spectrum of each towed body

为进一步抑制拖曳体2的升沉运动中，增加第二拖曳体的水深方向的附加质量系数，计算拖曳体的运动响应特征。在将第二拖曳体的附加质量系数设置为5,10,15,20，对比计算得到的谱特征曲线的部分特征段如图7所示。随着拖曳体的附加质量系数的增大，对传递而来的运动的响应越来越小，对比图6和图7可知拖曳体的运动特征逐渐趋向于只含有一个长周期的升沉运动，而水面端传递而来的振动频谱特征如谱密度峰值下降和分布规律。

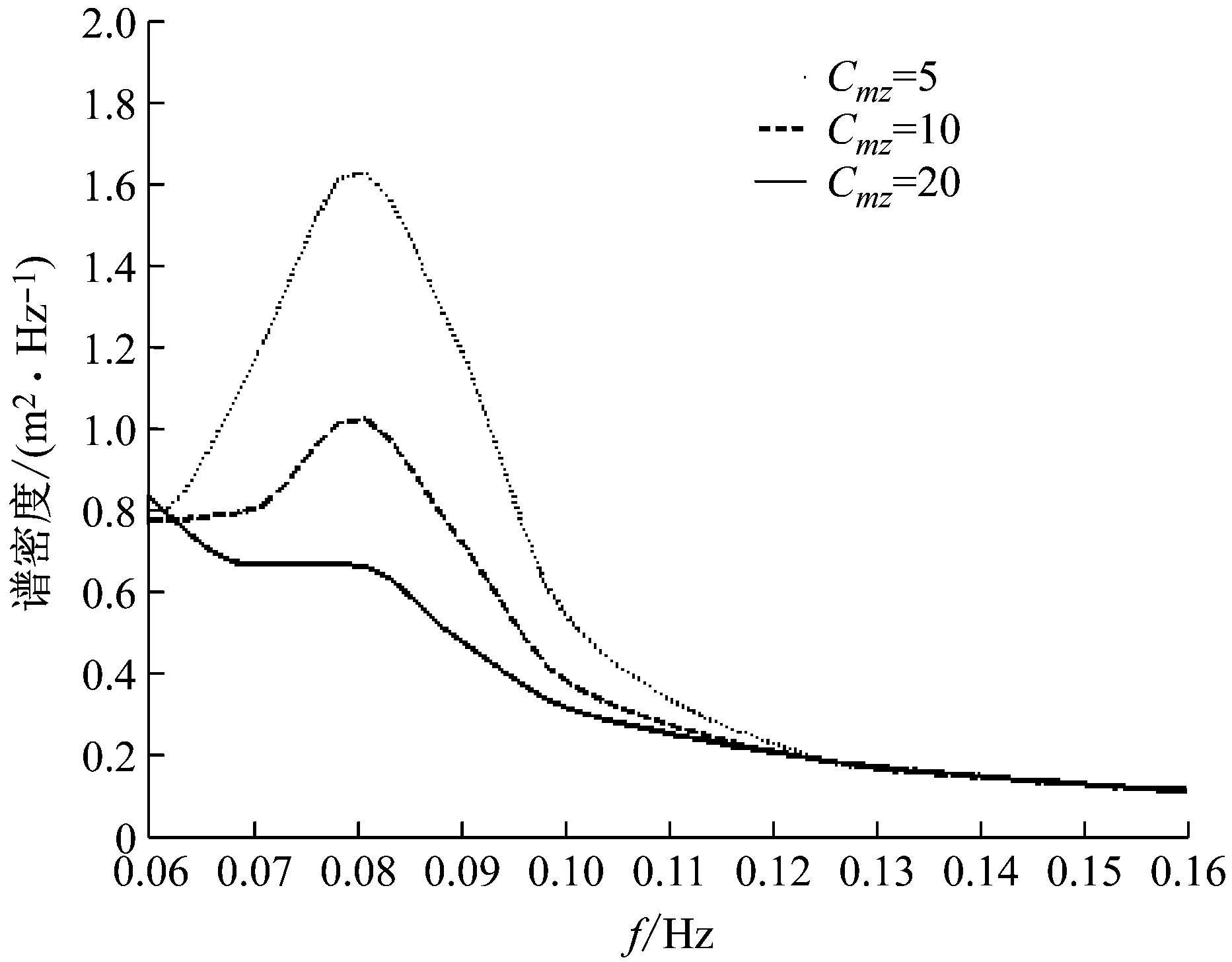
图7 不同附加质量系数对传递而来的运动的响应频率Fig.7 The responsible heaving spectrum of towed body with different added mass

2.2 多段式拖曳对随机振动的隔振效应

增加拖曳体水深方向的附加质量，使得拖曳体能够起到“滤波”作用，最终将随机振动的影响较好的隔离。在多段式拖曳系统中，改变各拖曳体的附加质量特征，由于缆的振动总是以沿着缆轴传递的纵向运动，以及沿着缆径的横向振动。经过第一个拖曳体对振动的传递形式的改变后，第二段缆内的振动转换成缆的横向振动为主，缆内的张力下降，通过增大第二拖曳体的水深方向的附加质量系数，这将使得横向振动的隔离效果增强。在随后的各段拖曳缆的设计中，通过增加多个用于隔振的拖曳体单元，进一步降低传递而来的振动，从而起到良好的隔振效果。在表1给出的设计参数的基础上，通过简单复制第一个尾巴段连接到尾端拖曳体来增加拖曳缆段和拖曳体的数量，模拟服从JONSWAP谱运动的传递和响应谱，结果见图8至图10。

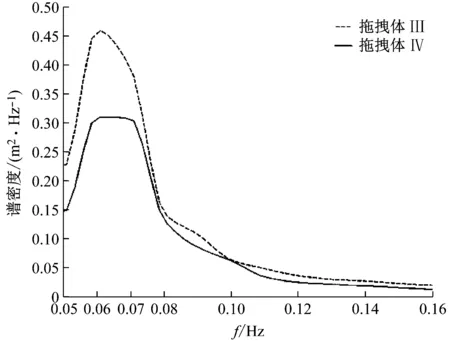
图9 三、四段式拖曳系统的尾端拖曳体运动响应频谱Fig.9 The heaving spectrum of each tail towed body in a three and four-sections towed system

图8对比了三、四、五段式拖曳系统中拖曳体2的运动频谱，可见随着缆段的增多，第二拖曳体的微幅运动逐渐趋向于服从JONSWAP谱运动的特征。这是因为拖曳段增多，使得第二段的拖曳缆的张力增大，缆段数量的增多那么第二段缆内的张力就会成倍增长，缆的刚度增强，对拖曳体1的运动传递效果的线性行为逐渐显著。而图9和图10显示了随后几个拖曳体的响应频率均逐渐减小运动缓和，这说明随后的缆段+拖曳体结构的运动响应逐渐呈现了非线性的响应规律，可见拖曳系统的非线性响应与缆内的张力呈反比。

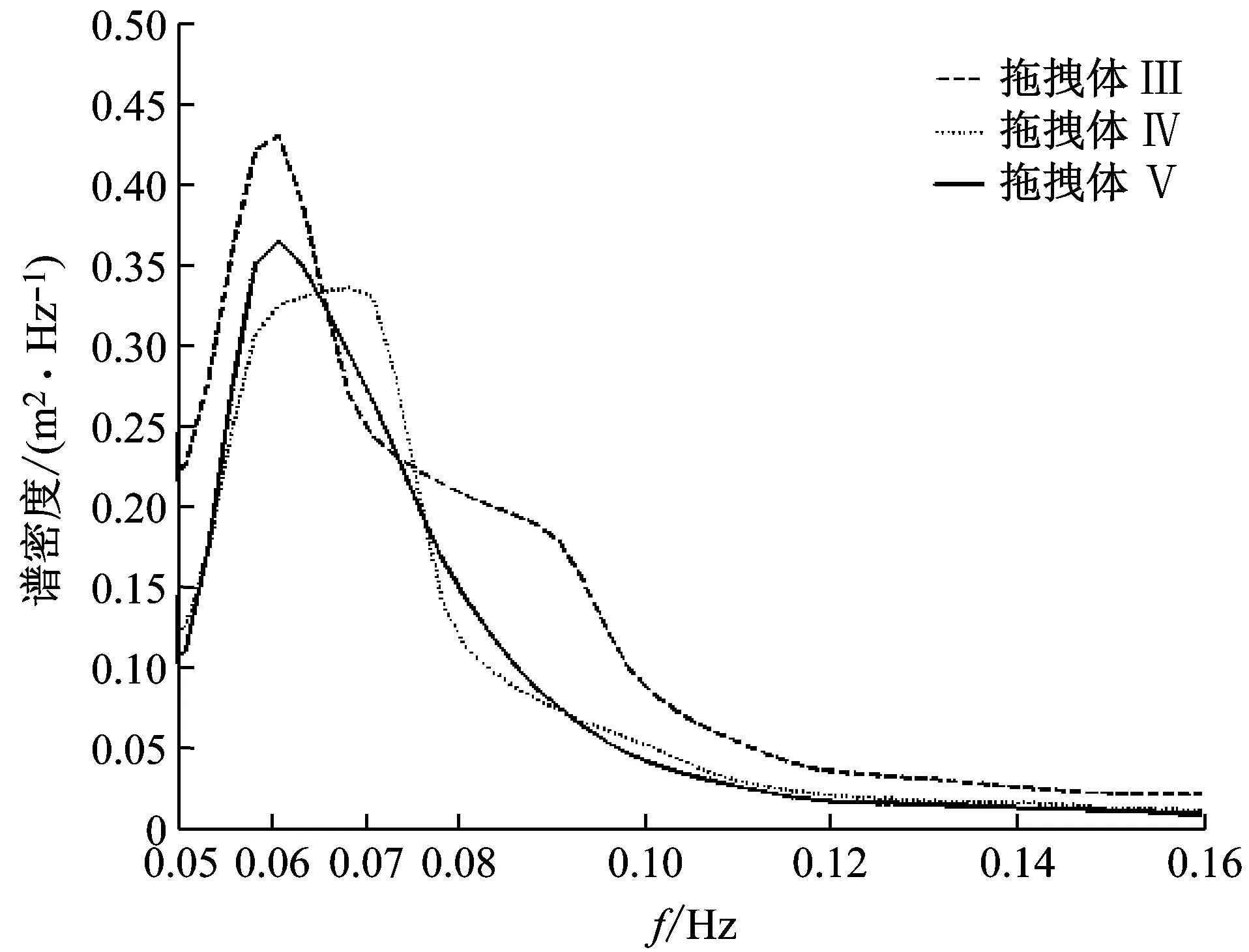
图10 五段式拖曳系统的尾端三个拖曳体运动响应频谱Fig.10 The heaving spectrum of three tail towed bodies in a five-sections towed system

3 结 论

(1)多段式拖曳系统对随机振动的隔振效应是通过缆段与拖曳体的水流阻尼衰减振动实现的，中性拖曳体的附加质量增强了隔振效应，改变了频率传递特性。

(2)拖曳缆运动传递的线性特征随着缆内的张力增大而逐渐显著，因此注重采用低水流阻力的设计降低拖曳缆内的张力，那么拖曳缆的阻尼效应将增强。

(3)拖曳体的垂向附加质量系数增大可起到较好的抑制振动的作用。