滑橇式直升机地面共振机体动力学特性研究

吴 靖，胡国才，刘湘一

(海军航空大学 航空基础学院,山东 烟台 264001)

滑橇式起落架以其结构简单、质量较轻、性能可靠等优点广泛应用于中小型直升机，其地面共振动稳定性研究是直升机动力学非常重要的课题，但针对滑橇式直升机特点的地面共振研究相对较少。

Walden等[1]对RQ-8A无人滑橇式直升机在鱼叉格栅系留的情况下进行了地面共振试验。Minderhoud[2]介绍了Bell429滑橇式直升机机身与起落架由四点连接改为后三点连接，能有效降低机体模态固有频率以改善地面共振稳定性，于仁业等[3]采用MSC软件计算了这两种连接方式下机体的固有频率，并对比了这两种连接方式下直升机的地面共振稳定性。Narramore等[4]对Bell429滑橇式直升机在常温(16 ℃)和低温(-39 ℃)时的地面共振动稳定性进行了分析，结果表明该直升机在较宽的温度范围内所有工作转速下都具有足够的模态阻尼，说明该直升机具有良好的地面共振动稳定性。关于滑橇式直升机地面共振的机体动力学特性分析一般采用有限元法，程金送[5]采用有限元法计算滑橇式起落架侧移和滚转的刚度及阻尼，并由此计算全机的有效质量、刚度及阻尼用于地面共振分析。Sharf等[6]利用ANSYS软件建立了滑橇式起落架的有限元模型，获得的机体质量、刚度及阻尼参数用于通过数学模型计算地面共振不稳定区，并利用该软件进行了旋翼/机体非耦合模态分析，结果发现增加起落架的高度有助于缓和直升机地面共振动不稳定性。徐敏等[7]提出了一种通过有限元方法获取机体动特性参数，并基于特征值法进行滑橇式直升机地面共振动稳定性分析的方法。

在无法确保直升机机体及滑橇式起落架具有足够的结构阻尼时，需要在机体与起落架之间布置阻尼器来增加系统阻尼，而局部增设阻尼器往往使系统成为非比例阻尼系统[8-9]。非比例阻尼系统模态之间的阻尼耦合将使得阻尼器阻尼对模态频率及阻尼的影响变得复杂[10-11]。

本文将建立支持在滑橇式起落架上的直升机有限元模型，结合有限元法给出直升机机体模态频率和当量至桨毂中心的质量、刚度及阻尼的计算方法，并分析机体阻尼器的非比例非线性阻尼对机体模态频率及阻尼的影响。

1 支持在滑橇起落架上的机体模型

直升机机体刚度大，其弹性对支持在起落架上的机体动力学特性影响较小，直升机地面共振研究中一般将其看作刚体，有限元软件(MSC)建模中采用多点约束单元(MPC)将重心与起落架连接点进行刚性连接，并通过在重心处施加集中质量及惯性矩模拟机体惯性。

滑橇式起落架刚度小、变形大，采用有限元方法进行建模，其前后横梁及左右橇管均采用梁(BEAM)单元模拟，横梁各处粗细不同，采用变截面形式，而橇管轴向截面积变化不大，采用统一截面形式。

在机体及起落架结构阻尼不够的情况下，需要在机体与起落架之间布置阻尼器来增加系统阻尼避免发生地面共振，有限元软件建模中采用阻尼单元(DAMPER)模拟。

一般在机体与起落架之间采用的阻尼器为液压阻尼器，而为防止载荷过大对结构造成破坏，通常设置定压安全活门，其动力学模型[12-13]为

(1)

式中：mv为阀芯质量；cv、kv分别为阀芯运动阻尼和刚度；x为阀芯相对阀座的位移；Av为阀芯受压面积；PL=P1-P2为活塞负载压强；P1、P2分别为液压缸右腔和左腔的压强；Cv为阀口流量系数；d为阀座内径；α为阀芯半锥角；F0为定压活门预压力；Qv为流经定压活门的油液流量；ρ=900 kg/m3为油液密度；i=1,2分别表示液压缸右腔和左腔；V1、V2分别为液压缸右腔和左腔的容积；β1、β2分别为液压缸右腔和左腔的油液体积弹性模量；Ap为活塞受压面积；s为活塞位移；Cd为阻尼孔流量系数；Ad为阻尼孔截面积；η为油液含气体积百分比；n=1.1～1.4为气体多变指数；Patm=0.101 MPa为大气压强；βe=1.38×109N/m2为在大气压下纯油液的有效体积弹性模量。

对某型液压阻尼器进行周期激励，采用式(1)计算其等效阻尼Ce及阻尼力峰值Fm随速度幅值的变化情况，结果如图1所示。

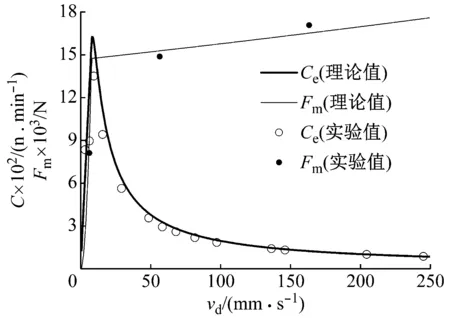
图1 液压阻尼器等效阻尼及阻尼力峰值Fig.1 Equivalent damping and damping force peak of hydraulic damper

由图1可知,式(1)计算所得的液压阻尼器等效阻尼及阻尼力峰值与实验数据吻合较好，说明了该模型的可靠性，有限元模型中阻尼单元的阻尼系数可采用该模型计算获得。

某型滑橇式直升机机体及起落架简化有限元模型如图2所示，节点1为重心，节点2为桨毂中心，节点3、4和5为机体与起落架连接点，节点6、7为阻尼器与机体的连接点，节点8、9为阻尼器与起落架的连接点。

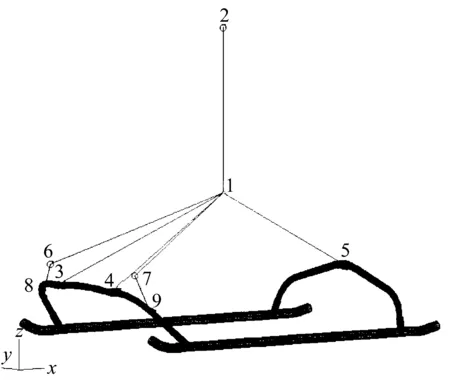
图2 滑橇式直升机机体有限元模型Fig.2 Finite element model of skid helicopter fuselage

2 机体动力学特性分析

2.1 无阻尼固有特性

在采用当量平面模型[14]进行直升机地面共振分析时，主要关注机体纵向(纵移和俯仰)和横向(横移和滚转)前两阶模态的固有频率、当量质量、当量刚度及当量阻尼，文中所指当量化均指当量至旋翼桨毂中心。机体模态瞬心位置、当量质量[15]及当量刚度的具体计算如下

(2)

式中：j=1～4分别表示纵移、俯仰、滚转和横移模态；zj为机体第j阶模态瞬心位置，数值为正在重心以上，数值为负则在重心以下；xj和φj分别为机体第j阶模态下重心平动量和转动量；mj为机体第j阶模态当量质量；Ix和Iy分别为机体纵向和横向惯性矩；mf为机体质量；zh为桨毂中心到机体重心的高度；kj为机体第j阶模态当量刚度；ωj为机体第j阶模态固有频率，该频率为无阻尼固有频率。

某型滑橇式直升机机体主要参数如表1所示。

表1 机体主要参数Tab.1 Main parameters of fuselage

采用有限元软件(MSC)计算该滑橇式直升机机体无阻尼时的模态固有频率及各模态下重心平动量和转动量，根据式(2)计算机体模态瞬心位置及当量质量如表2所示。

为分析阻尼器对各机体模态的影响，现将机体重心、阻尼器及各模态瞬心位置表示如图3。

将机体固有特性当量至桨毂中心，实际上是将系统等效成了比例阻尼系统。对于比例阻尼系统，先通过有限元软件求得系统复特征值，根据复特征值可得机体模态固有频率及阻尼比为

表2 机体无阻尼固有特性Tab.2 Natural features of fuselage without damping

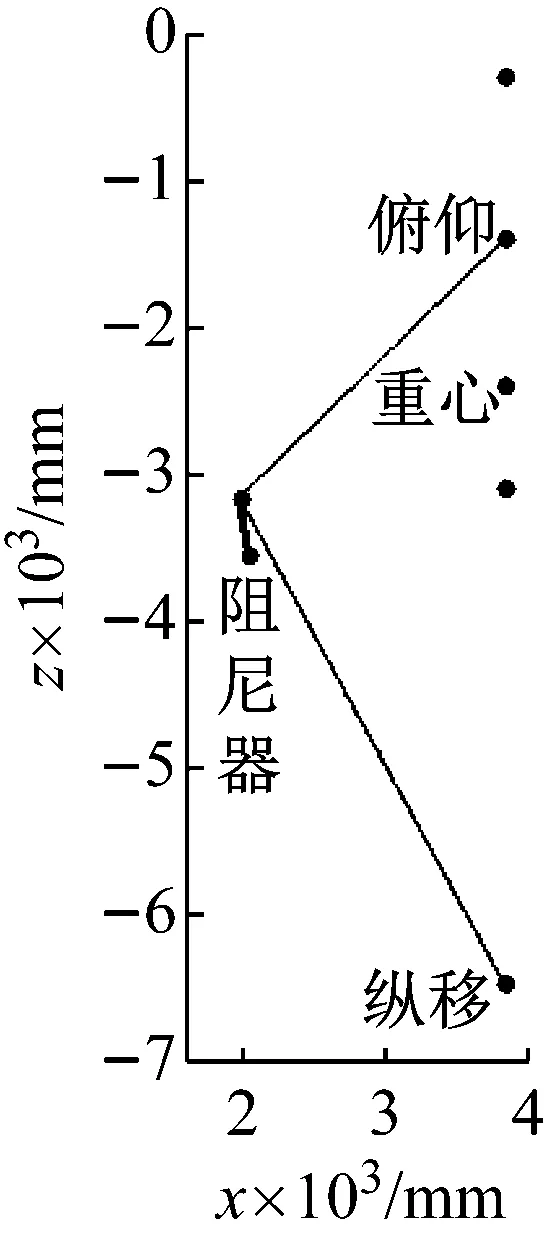
图3 机体重心、阻尼器及各模态瞬心位置Fig.3 Location of gravity center,damper,and modal instant centers

(3)

式中：s1j和s2j为系统第j阶模态复特征值对；ξj为机体第j阶模态阻尼比。

根据式(2)所得当量质量和式(3)所得固有频率及阻尼比可得当量阻尼为

cj=2mjωjξj

(4)

式中：cj为机体第j阶模态当量阻尼。

对于局部设置阻尼器的非比例阻尼系统，先求系统复特征值，再采用式(3)计算得到的无阻尼固有频率，文献[11]为与无阻尼系统固有频率区分，称之为伪无阻尼固有频率，对于比例阻尼系统，这两个固有频率相同。阻尼器取不同阻尼时的伪无阻尼固有频率(粗线)及阻尼振动频率(细线)如图4所示。

由图4可知，伪无阻尼固有频率及阻尼振动频率会随阻尼器阻尼的增加而变大，其中俯仰和滚转模态变化尤为明显，从图3分析可知，在图示位置布置阻尼器时，该两阶模态瞬心与阻尼器的连线和阻尼器的夹角更接近90°，阻尼器对该两阶模态作用更大，因此其阻尼的改变对这两阶模态的固有频率影响较大。为计入阻尼器非比例阻尼的影响，在采用式(2)计算当量刚度时，无阻尼固有频率应取伪无阻尼固有频率。

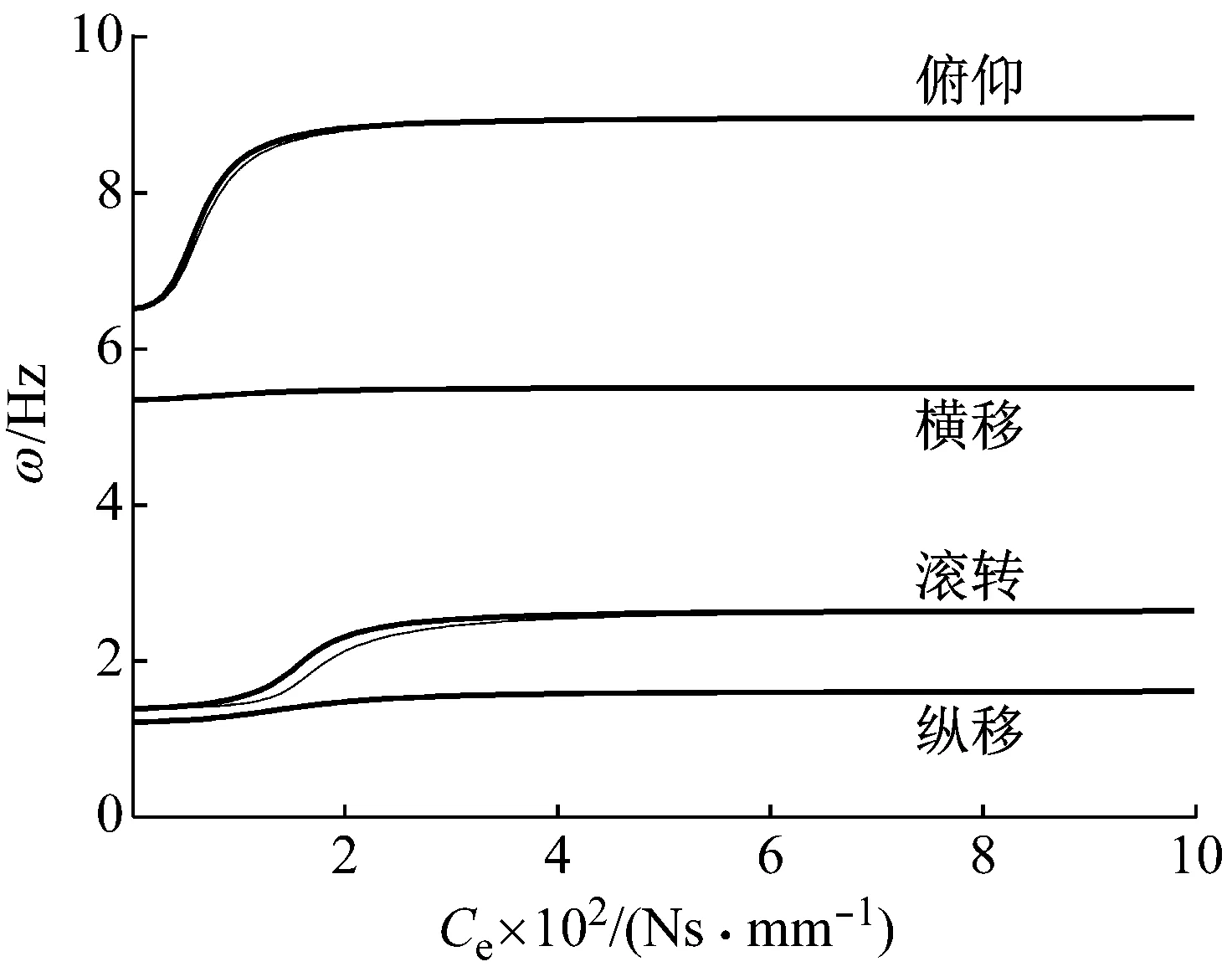
图4 系统振动频率Fig.4 Vibration frequency

2.2 模态阻尼比及当量阻尼

由表2可知，机体俯仰和横移模态固有频率较高，与旋翼摆振后退型模态的共振转速约为500 r/min和570 r/min，离该直升机旋翼工作转速较远，可以不予考虑，而机体纵移和滚转模态与旋翼摆振后退型模态的共振转速约为250 r/min和260 r/min，接近该直升机旋翼额定转速，因此后文将重点关注机体纵移和滚转模态。采用式(3)复特征值法求解的机体纵移和滚转模态阻尼比随阻尼器阻尼的变化如图5所示。

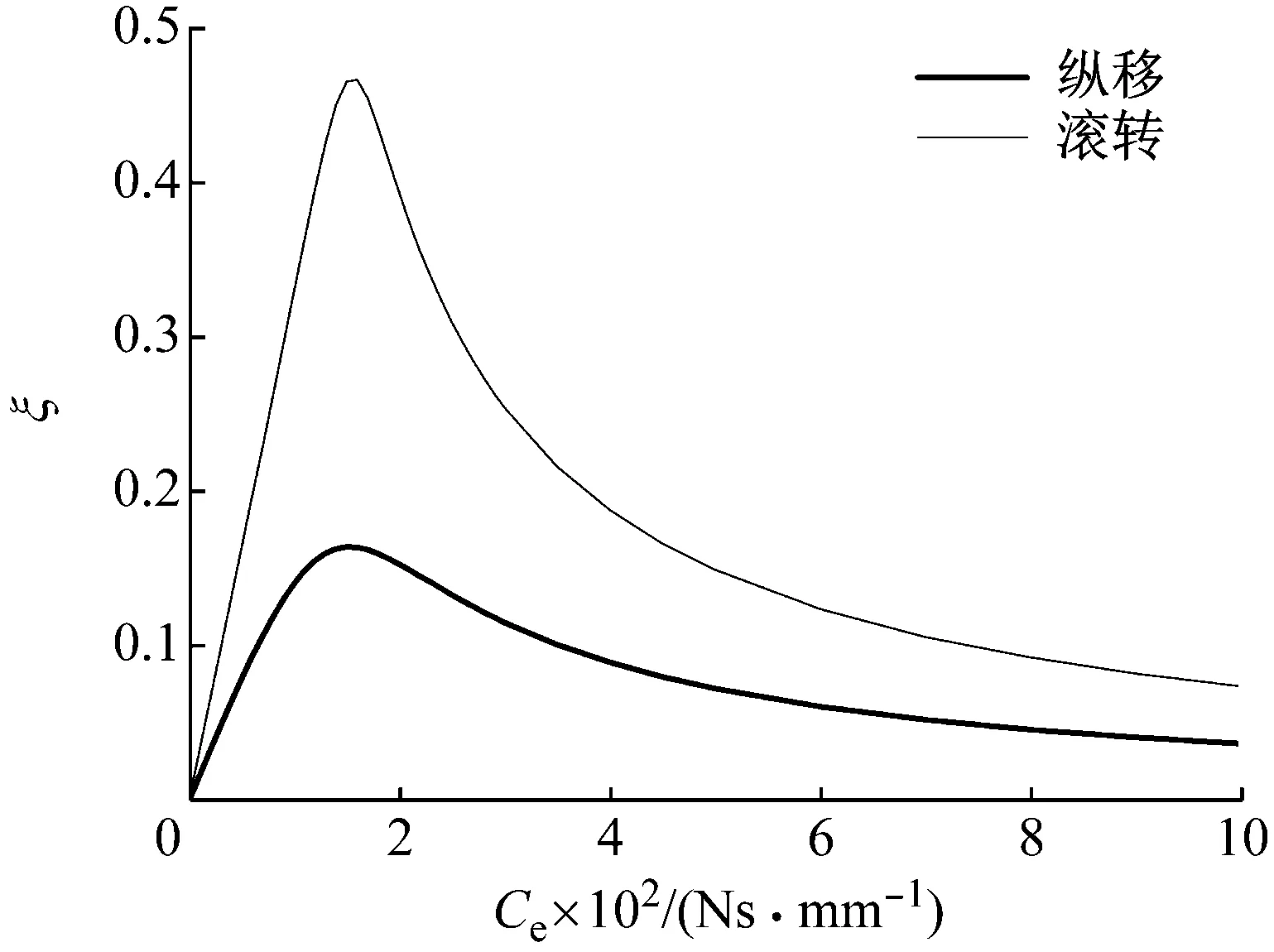
图5 系统模态阻尼比Fig.5 Modal damping ratio

在不考虑机体及起落架的结构阻尼，只考虑机体阻尼器阻尼的情况下，当量阻尼即阻尼器当量至桨毂中心的阻尼Chd，由式(4)计算的当量阻尼如图6所示。

由图5、图6可知，在阻尼器取小阻尼时(Ce<100 Ns/mm)，机体纵移和滚转模态的阻尼比和当量阻尼随着阻尼器阻尼增加近似呈线性增加的趋势，分析可知阻尼器阻尼越小，非比例阻尼系统模态之间的耦合越弱，也就说明在阻尼器取小阻尼时，该系统可近似看作比例阻尼系统；而在阻尼器阻尼增加至一定值时(Ce>180 Ns/mm)，系统的模态阻尼比及当量阻尼将呈衰减的趋势，分析可知是非比例阻尼增加使得各模态之间耦合增强引起的，该种耦合对于直升机地面共振是一种不利影响。

图6 当量至桨毂中心的阻尼Fig.6 Equivalent damping to rotor hub

综上所述，采用式(2)、式(4)将机体固有特性当量至桨毂中心时，系统的固有频率应取计入阻尼器非比例阻尼影响的伪无阻尼固有频率；当量阻尼则通过复模态命令求解复特征值后根据式(3)、式(4)计算，这样能使当量后的比例阻尼系统与实际非比例阻尼系统具有相同的复特征值。

2.3 阻尼器非线性的影响

计入液压阻尼器阻尼关于速度的非线性后，结合有限元法采用复特征值计算机体模态频率及当量阻尼的流程如图7所示。

图7 计算当量阻尼流程Fig.7 Calculation flow of equivalent damping to rotor hub

在液压阻尼器某一速度下由图1中等效阻尼—速度曲线确定阻尼器阻尼后，由有限元软件的复模态命令求解复特征值后根据式(3)计算模态固有频率及阻尼比，再根据式(4)计算当量至桨毂中心的阻尼。

图8、图9分别为根据上述方法计算的计入阻尼器非线性时的机体模态频率及当量阻尼随阻尼器速度的变化曲线。

由图1可知，在阻尼器活门未开启之前，其等效阻尼随着速度的增加近似呈线性增加的趋势，因此在图8中显示的模态频率变化趋势与图4中类似，图9中显示的当量阻尼变化趋势与图6中类似；阻尼器速度增加至活门开启后，其等效阻尼近似呈反比例函数的趋势减小，由图4可知模态频率随着阻尼器阻尼的减小而减小，若实际阻尼器最大阻尼大于当量阻尼开始减小时的阻尼器阻尼(180 Ns/mm)，由图6可知当量阻尼随着阻尼器阻尼的减小将先增加后减小，图8中活门开启后模态频率及图9中当量阻尼的变化趋势符合该规律。

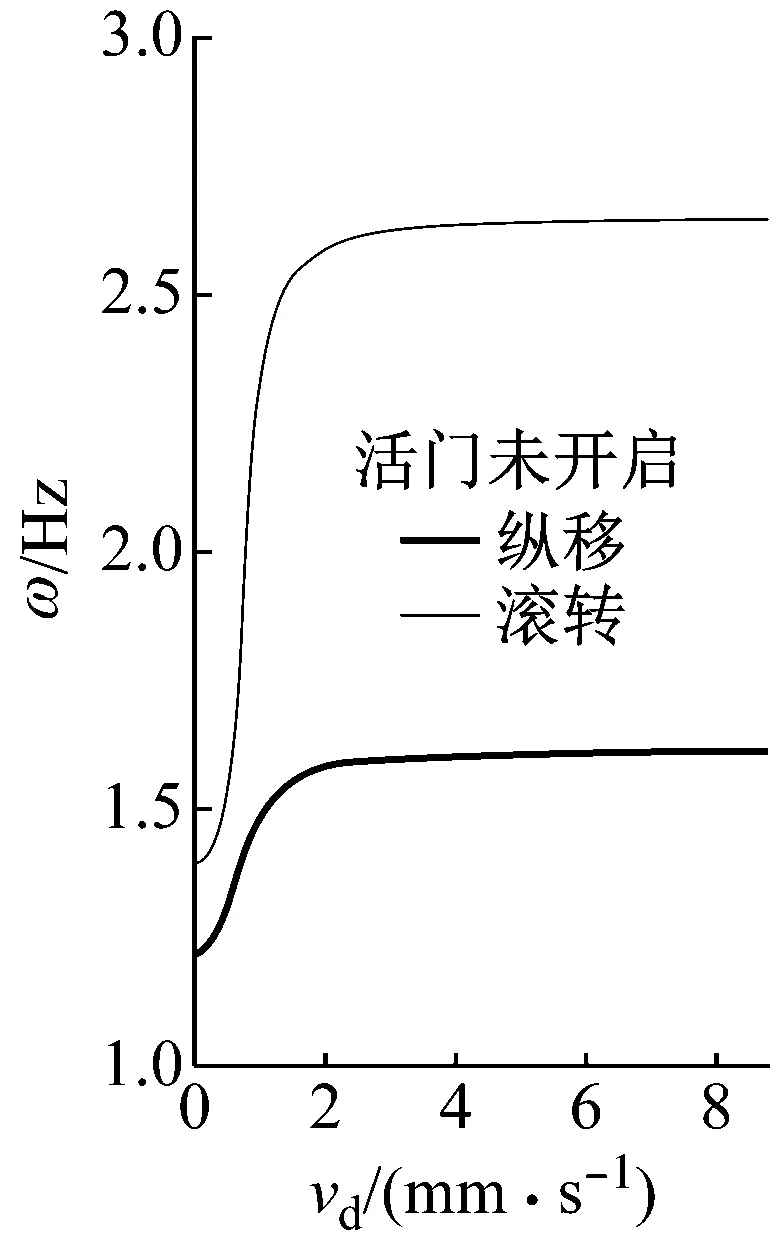
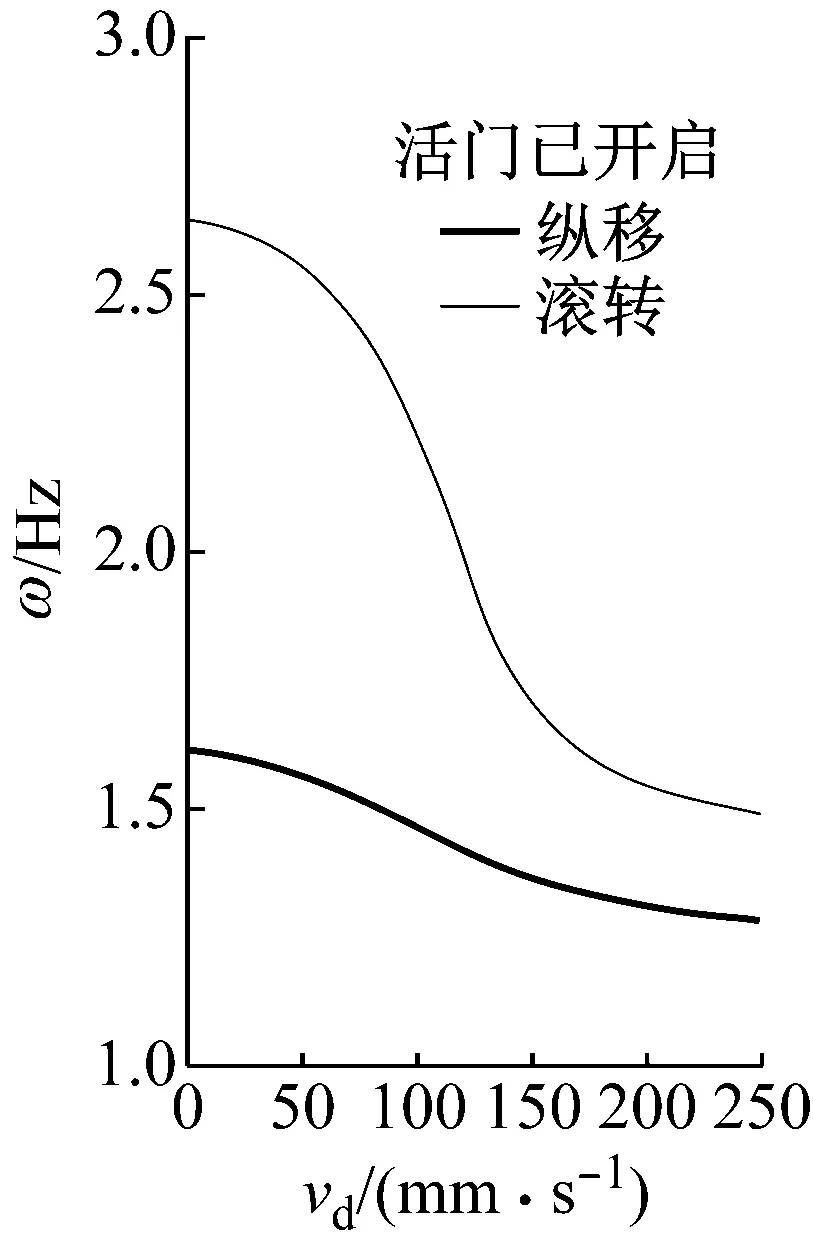
图8 模态频率随阻尼器速度变化曲线Fig.8 Changing curves of modal frequency with damper velocity

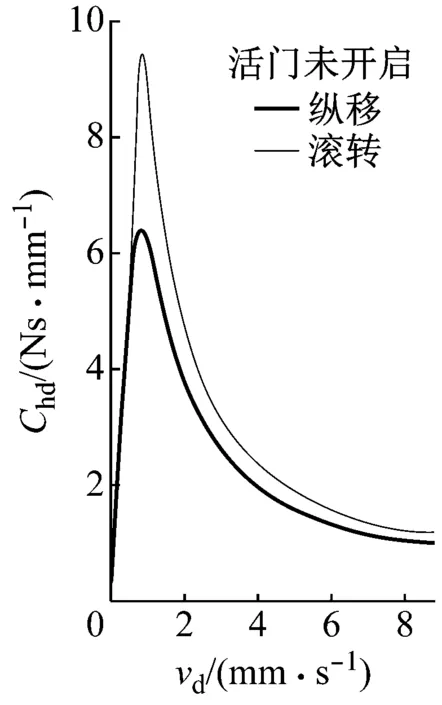
图9 当量阻尼随阻尼器速度变化曲线Fig.9 Changing curves of equivalent damping to rotor hub with damper velocity

3 结 论

(1)将机体固有特性当量至桨毂中心时，系统的固有频率应取计入阻尼器非比例阻尼影响的伪无阻尼固有频率，当量阻尼则通过复模态命令求解复特征值后根据式(3)、(4)进行计算，这样能使当量后的比例阻尼系统与实际非比例阻尼系统具有相同的复特征值；

(2)由于非比例阻尼的影响，使得机体模态频率随阻尼器阻尼的增加而增加，而在阻尼器增加到一定程度时，机体模态阻尼可能减小，不利于直升机地面共振动稳定性；

(3)计入阻尼器阻尼关于速度的非线性后，模态频率随阻尼器速度的增加先增加后减小，模态阻尼不是按照阻尼器阻尼随其速度的变化趋势而变化，而可能出现两次增加再减小的过程，在阻尼器定压活门开启前后各形成一个峰值。

文中给出的当量化处理方法是否可行取决于系统复特征值求解的准确性，而复特征值是通过有限元仿真软件求得，若能得到实验的进一步验证，将有益于指导滑橇式直升机的地面共振动稳定性设计。