处理圆锥曲线“对称性”问题策略之刍议

王平

例：已知椭圆C：3x2＋4y2-12=0，试确定m的取值范围，使得对于直线L：y=4x＋m，椭圆C上存在不同的两点关于直线对称。

分析（1）：首先由数形结合，抓好特征量，特征线及关键词，垂直且平分还有存在。设而不求思想搭好台，用垂直引领得出AB直线方程，y=，在存在两个不同的点的前提下获悉不等式来唱戏，问题不但得以解决，还留下经典的解题套路。

解法一：设A（x1，y2），B（x2，y2），由AB与L对称，故可设AB为：y=联列方程组

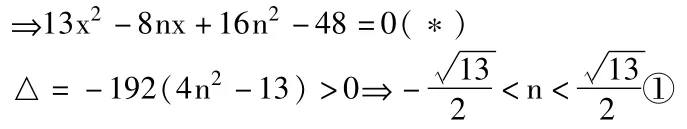
又∵AB的中点在直线L上，由（※）可知

分析（2）：凡涉及到中点弦问题，自然由点差法来搭台，进而求得AB中点坐标的含参表达式，确定取值范围的不等关系聚焦在点与圆锥曲线的关系。更为明确地点在椭圆之内，由此又得到解决此类问题的另一典型套路。

解法（2）：设C上关于L：y=4x＋m的对称点分别为A（x1，y1），B（x2，y2），设AB的中点为P（x0，y0），由此有

又∵P（x0，y0）在L：y=4x＋m上⇒y0=4x0＋m ④

由③、④解得x0=-m y0=-3m ∵P（x0，y0）在C的内部

分析3：关键词是存在两个不同的点，由此应该是某个含参的二次方程在区间-2≤x≤2有两个相等实根，由区间根的分布来搭桥，不等式唱戏，便可以顺利解决。

有两个不相等的实根，作辅助函数L（x）=13x2＋26mx＋169m2-48 x∈［-2，2］，由区间根的分布：

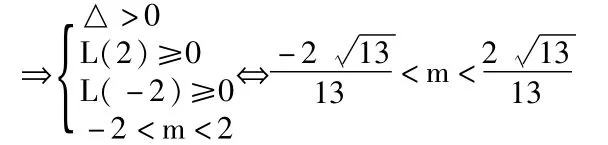
分析（4）：直接由二-级结论搭桥引线，圆锥曲线中椭圆任一不垂于x轴的弦的斜率与弦的中点与坐标原点的斜率之积为定值，由此便可解决。

解法4：设A（x1，y1），B（x2，y2），AB的中点m（x0，y0）

∵KAB·KOM=

⇒y0=3x0（-2＜x0＜2）

弦中点M的轨迹仅为线段且不含有端点：

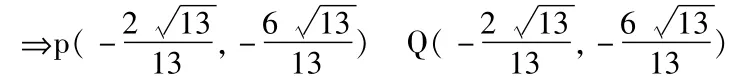
总之，要让我们高三复习依标扣本，源于教材，又高于教材，要求课堂教学中，搭好思想与方法的桥，唱好探求方法多样性的戏。充分利用好二级结证，学生思维才能进阶，学生在课堂才会走心入神，形成一种探求习惯及运用教学思想的意识，搭台唱戏的思想平台，准会让学生站在思维的制高点上，形成运用意识。