低结构教学高思维发展——以《平行四边形与梯形练习》教学为例

周珊珊

学生数学学习能力的提升，数学思维层次的提高，不是通过教师的精心预设、反复打磨、多次试教来实现的。真正的教学应是由学生发起，并满足学生内在需要的师生和谐的互动过程。低结构教学，一场教学观的变革，在遵循数学知识内在的联结中促进全体学生自主全程参与，体验由浅入深、由外而内的学习方式，进一步引发学生深层次的思维。下面笔者以人教版《平行四边形与梯形练习》一课为例，诠释低结构教学激活学生高思维发展的课堂教学策略。

【片断一】低情境导入，高空间发展

课件出示：点A（你看到了什么？）（一个点）依次出示：点B、C、D，如图1 所示。

图1

图2

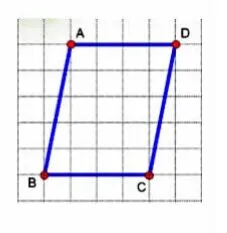
图3

师：把这4 个点依次连起来，会是什么图形？（异口同声：平行四边形）都认为是平行四边形，对吗？（对）

师：（课件出示图2）真是平行四边形吗？

师：怎么回事？怎样才能变成平行四边形？

生：把D 点往上移。

师：随便移吗？

生：不能，要移到D 点上面的方格交叉点上。

师：（课件出示图3）为什么？

生：两组对边分别平行的四边形。

师：（课件演示）如果老师把点D 继续往左移并把四点依次连起来，会是什么图形？（梯形）

师：为什么不是平行四边形了？（只有一组对边平行的四边形）继续移动点D，图4 是什么图形？（直角梯形）为什么？（有一个角是直角）

师：继续移动点D，图5 什么图形？（三角形）

图4

图5

图6

师：继续向左移动点D 呢，图6 是什么图形？（梯形）

师：点D 在这条线上移动的过程中，你有什么发现吗？

生：AD 和BC 始终是互相平行的，当另一组边也互相平行时就是平行四边形，当另一组边不平行时就是梯形，A 和D 两个点重叠在一起时就是三角形。在变化的过程中，它们的高始终不变。

【说明：这节练习课的导入从最基本的点开始，把四点依次连接，造成共性认同，一致认为连成之后是平行四边形。教师借助方格图，引发原认知冲突，学生重新梳理、回顾平行四边形的特征，及时巩固强化。这样低结构的情境导入，不仅有效沟通了平行四边形与梯形之间的关系，强化了平行四边形与梯形的特征，发展了学生的空间想象力，更是让学生在变与不变中沟通图形之间的联系。】

【片断二】低自主练习，高思维激发

课件出示：在每个平行四边形中添上一条线段，把它分割成两个完全相同的图形。如图7 所示。

图7

师：读一读，这道题主要有几个要求？（1.添一条线段；2.分割成两个完全相同的图形）

师：请每位同学在练习纸上动手分一分、画一画。（学生在练习纸上按要求自主练习，教师选取学生不同的作品在黑板上张贴出来）

师：大家看，你们的分法和这些同学的方法一样吗？还有不同的分法吗？如果把这些画法进行分类，你会怎么分？（两个完全相同的三角形、平行四边形、梯形三类，如图8 所示）

图8

师：一个平行四边形可以分成两个完全相同的三角形、平行四边形、梯形。反过来可以怎么说？（两个完全相同的三角形、平行四边形、梯形可以拼成一个平行四边形）

师：既然两个完全相同的图形可以拼成一个平行四边形，那么其中一块的大小与平行四边形有什么关系？（其中一块的大小都是平行四边形面积的一半）

师：同学们在分割过程中，分成两个什么图形最容易？（三角形）为什么？还有两种呢？（要用尺量一下，有点麻烦）有没有可能不量，也像分割三角形一样随意画一条线，就一定能分出两个完全相同的图形？（同桌讨论怎么画线）

生：先画出平行四边形的两组对角线，中间的交叉点就是这个平行四边形的中心点，我们只要过这个中心点随意画线，就一定可以分出两个完全相同的图形。如图9。

图9

【说明：在这个环节中教师准备了一道基本的、开放性的操作题，使所有学生都参与，留足思考的空间和时间，所有学生都可以提出自己的想法、建构自己的所学。探究过程中，学生亲身发现了知识的联结点，沟通了平面图形之间的关系，还为今后的面积教学做好铺垫。低结构教学，学生不再被动地接受知识，而是积极自主地参与学习，在活动中学会学习。让学生通过自己的理解、观察、发现、体验和反思去拓展知识，实现对知识的再认识、再理解，完成转识成智的过程。】

【片断三】低结构预设，高拓展延伸

师：四边形除了都有4 条边，还有4 个角。出示图10，大家算算这两个四边形它们的内角和各有多少度。

图10

师：我们在练习十一中通过测量知道四边形的内角和是360°。从内角我们会想到外角。你知道四边形的外角在哪里吗？（学生猜想并指出）

师：一般我们把每条边的延长线与另一条边组成的角看作外角。（课件逐次呈现长方形外角，如图11 所示）长方形外角有几个？它们的和是多少？（90°×4=360°）

图11

图12

师：观察每个内角和外角之间有什么关系？（加起来是平角，是180°）

师:平行四边形的四个外角在哪里？它们的和是多少呢？（小组探究）

生：如图12，平行四边形一个内角和一个外角的和是180°，有这样的4 组。用4 个平角的和减去平行四边形的内角和360°就是它的外角和了。算式是180°×4-360°=360°。

师：那么梯形的外角和是多少呢？（和平行四边形外角和思路一样，也是180°×4-360°=360°）

师：对四边形的外角和你们有什么猜想？（四边形的外角和是360°）

师：真的是这样吗？你还想到了什么？

生：我还想到可以用四边形内角和与外角和的办法，去计算出五边形、六边形的内角和与外角和……

【说明：从内角和到外角和的探究，从四边形外角和到多边形外角和的推想……这样低结构、开放式的教学，引领每一个学生去思考、去观察、去发现，学生和学生之间产生有效的思维互动，实现课堂思维拓展最大化。】

低结构教学，高思维发展，不仅教会学生数学知识，更重要的是教会学生学会学习，让学生在学习中发展数学思维，培养创造性思维。低结构教学，高思维发展，让数学课堂教学成为一个动态的、交互的、思维激荡的自主建构过程。