基于监测数据的岸桥模态参数识别

2019-10-30 08:43秦仙蓉余传强孙远韬

振动与冲击 2019年20期

秦仙蓉，余传强，孙远韬，宗瑞，张氢

(同济大学机械与能源工程学院，上海 201804)

岸边集装箱桥式起重机(以下简称岸桥，如图1所示)为集装箱船与码头前沿之间装卸集装箱的专用设备，其结构性能的可靠性与稳定性显得尤为重要。然而在长期使用中由于各种载荷作用以及环境侵蚀等各种因素的影响，其结构性能将发生改变，通过对岸桥进行长期监测，了解其不同状态下的动力学特性对于保证其安全工作，显得尤为重要。

通过有效的参数识别方法能得到结构的相关参数，从而掌握大型结构的健康状况。其中随机子空间法是环境激励下时域的主要模态参数识别方法之一[1-2]，该方法最早由Juang与Pappa应用于结构模态参数的识别中[3]。随机子空间法不需要人为激励，可以直接从环境激励的响应输出信号中获取结构的模态参数。该方法的关键是如何准确的确定系统的阶次，稳定图法是一种较好的方法，该方法可以从诸多的模态中辨别真假模态从而便于剔除虚假模态[4]。

图1 岸边集装箱桥式起重机Fig.1 Quayside container crane

目前，随机子空间参数识别法在桥梁和大型建筑上得到了广泛的应用。常军等[5]将随机子空间法运用在南京长江三桥的南塔的模态参数识别上，不仅准确地识别出了前四阶固有频率，还识别出较精确的阻尼比。徐良等[6]将该方法运用在了悬索桥的模态识别上，能有效地识别出10个在0.5 Hz以下的自振频率，并且得到较好的结构阻尼，验证了该方法在分析大型桥梁特征参数上的实用性。秦世强等[7]将经验模态分解与随机子空间参数识别相结合，将环境激励下的振动信号分解为一系列本征模态函数后利用随机子空间方法识别出了桥梁的模态参数，同时有效的抑制了虚假模态。臧廷朋等[8]也将经验模态分解与随机子空间参数识别相结合，有效的识别出了运行工况下转子系统的前两阶固有频率。谢伟平等[9]将随机子空间识别鲜见的运用到了宽幅钢箱梁桥的参数识别上，识别出了桥梁的前十二阶模态，并依据该模态识别结果结合响应面法对有限元模型进行了修正。杨风利等[10]通过随机子空间参数识别方法不仅识别出了格构式输电塔在脉动风激励下的频率，同时有效的识别出了该塔的阻尼比特性。

然而，目前国内对于岸桥这类大型重载机械的参数识别研究较少，且研究大都基于已知工况下的实测数据，研究工况较为单一。而实际工程中，岸桥的起制动频繁，工况复杂，虽然岸桥长期处于工作状态，但当遇到台风或者故障检修时则需要停机，此时处于非工作状态下的岸桥模态参数识别结果可能与岸桥处于工作状态下识别出的结果存在差异。因此，本文着重研究岸桥的不同工作状态对随机子空间法模态参数识别结果的影响。本文以上海洋山港1号集装箱码头某岸桥为研究对象，通过在其关键位置布置速度传感器，对其进行长期的健康监测，通过监测数据，利用随机子空间方法对该岸桥的频率、阻尼比和振型进行参数识别。

1 随机子空间识别方法

系统的振动方程可以描述为：

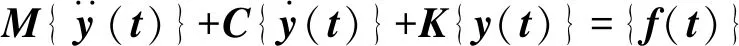
(1)

式中:M、C、K分别是质量、阻尼和刚度矩阵，{y(t)}是位移列阵，{f(t)}是载荷列阵。

用状态空间法对其进行描述为：

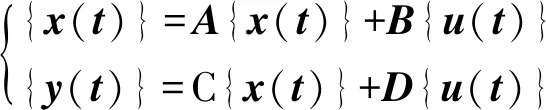
(2)

式中:A为状态矩阵；B为输入矩阵；C为输出矩阵；D为直接传输矩阵，{x(t)}为状态向量；{u(t)}为输入向量。

上述状态空间方程是连续的，而实际应用中，测试数据在时间上都是离散的，同时必须考虑随机因素-外界环境激励的干扰。因此将上述状态空间方程离散化并考虑随机因素就得到了离散化状态空间模型[4]：

(3)

式中:{x(k)}={x(kΔt)}为离散时间k时刻的状态向量；{ωk}是由环境激励和建模不精确而引起的过程噪声；{vk}是由传感器不精确或环境对传感器的影响而引起的测量噪声。这里均假设为零均值的白噪声序列。

随机子空间参数识别方法主要是通过求解状态空间矩阵A的特征值问题获得系统的码模态参数，该方法的简要过程如下：

(1)将测量数据构造Hankel矩阵，按矩阵行数的不同将其分为“过去”和“将来”构造新矩阵Y=Yp/Yf[11]；

(2)利用Yf、Yp构造Toeplitz矩阵形式的协方差矩阵：

(4)

(3)对上述协方差矩阵进行奇异值分解得到可观测矩阵Oi和可控矩阵Γi[12]：

T1/i=UiSiVi

=OiΓi

(5)

(4)根据Oi的推移不变特性可以计算出状态矩阵A：首先对协方差矩阵T1/i进行时延得到T2/i+1，可以发现T2/i+1=OiAΓi。此时系统状态矩阵为：

(6)

(5)求解状态矩阵A的特征值问题即可得系统的模态参数[13]。

A=φΛφ-1

(7)

(8)

式中:Δt为采样间隔。因此，系统的模态频率与阻尼比为：

(9)

系统的振型为：

ψ=Cφ

(10)

2 岸桥振动监测

2.1 监测过程

本文的数据采集自上海洋山港1号集装箱码头某岸桥，其主体结构由门框系统、门框连接系统、拉杆系统、梯形架以及主梁等组成。该岸桥整机高度大约78 m，其前大梁长度约71 m，小车轨道以上高度29 m，后大梁长度约31 m。岸桥小车空载时的质量为100 t，小车额定速度为4 m/s。工作时，小车与吊重及货物(重约165 t，约为整机质量的11.38%)以恒定速度(平均速度约为3.5 m/s)在大梁上移动；非工作时，小车停靠在泊车位，即中大梁靠后位置。

为了获得岸桥的振动信号，采用防水型磁电式速度传感器采集结构响应，传感器通过底部的4个磁力支座安装于岸桥的对应测点。X方向定义为小车运行方向，陆侧指向海侧为正方向；Y方向定义为竖直方向，竖直向上为正方向；Z方向定义为大车行走方向，根据右手法则确定正方向，如图2(a)所示。

根据有限元分析结果，在岸桥上布置10个速度传感器对其进行监测，10个速度传感器的布置位置依次为：梯形架顶部(A)、后大梁陆侧端点(B)和(C)、中大梁中点(E)、陆侧上横梁端点(D)以及海侧上横梁端点(F)，如图2所示。由于前大梁实际中有时会需要抬起(见图2(a)虚线)，故不宜布置传感器。传感器通过铠装防水信号线与布置于机器房中的信号采集仪相连。其中，A、D、F三个测点采集X方向数据，B、C、E三个测点采集Y方向数据，A、C、D、F四个测点采集Z方向数据。

图2 岸桥传感器布置图 Fig.2 Layout of velocity sensors

图3和图4是数据采集仪采集到的X，Y，Z三个方向部分测点的响应数据的时程曲线，响应信号的采样频率为200 Hz，采样方式为连续采样，每次连续采样一个月之后去现场取回数据，本文截取其中一段250 s的数据进行分析。

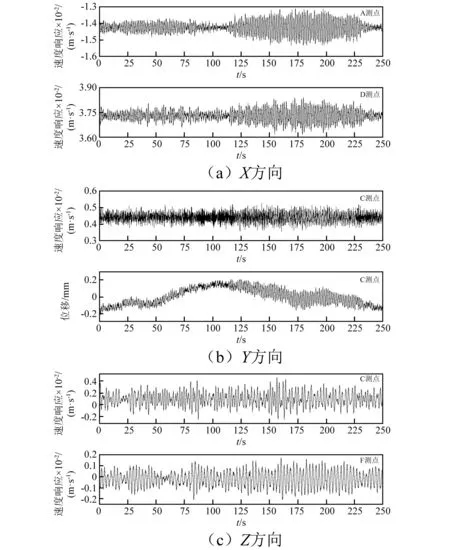
图3 非工作状态部分测点时程曲线Fig.3 Time history of non-working state responses

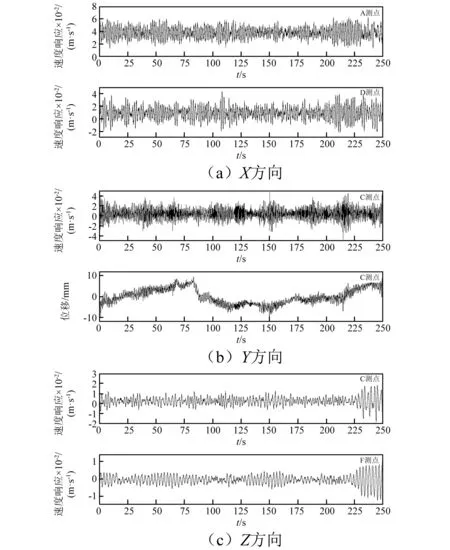
图4 工作状态部分测点时程曲线Fig.4 Time history of working state responses

由于监测数据是长期不间断采样，期间没有人员，因此如何准确的判断出一段连续的信号中哪部分是岸桥处于工作状态，哪部分是岸桥处于非工作状态对后期的参数识别有着至关重要的影响。本文通过对初选数据段进行积分得到各测点的位移信息，通过关键测点的位移值判断该段信号所处的工作状态。当岸桥工作时，小车与重物运行在大梁上，因此大梁的Y向位移应较非工作有明显的区别。图3(b)和图4(b)是岸桥C测点(位于后大梁右侧端点)Y方向的速度响应及积分得到的位移响应时程曲线，通过位移值可以明显的发现，工作状态下该测点Y向的位移为±10 mm，而非工作状态下该测点Y向的位移仅为±0.2 mm，因此，可以判断出两组信号对应的岸桥的工作状态。

2.2 岸桥的模态参数识别

图5的(a)和(b)分别是基于协方差驱动随机子空间法得到的岸桥在非工作状态下和工作状态下的试验模态识别稳定图。图5中，○是基于状态空间矩阵求解特征值问题得到的系统在不同的假定模型阶次的系统频率。为了能够有效地判别虚假计算模态，本文在稳定图中“叠加”了不同阶次的振型的模态置信因子(MAC)，当高阶模型的振型与低阶模型的振型的模态置信因子高于90%，则认为该点为稳定点(图5中用·表示)，从而使得模态的判别更加可靠。

由图5的(a)和(b)可以看出在1 Hz以内有非常明显的五条纵向稳定轴，分别对应于岸桥的五阶固有频率。图6的(a)和(b)为岸桥在非工作状态和工作状态下识别得到的频率和阻尼比的分布特征。根据图6中的分布可以看出，频率和阻尼比都离散的分布在一定的区间内，其中频率的离散程度非常小，阻尼比的离散程度较频率略大。

图5 岸桥试验模态识别的频率稳定图Fig.5 The identified stabilization diagrams of QCC

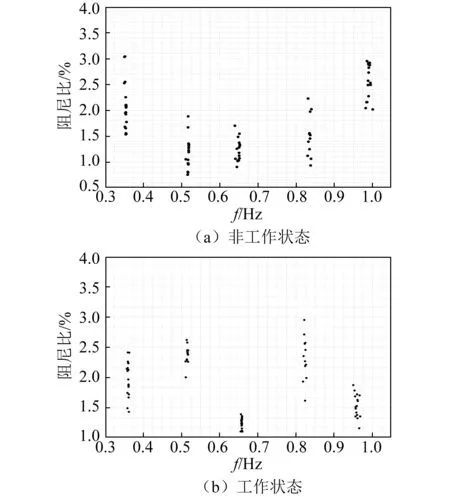
图6 岸桥试验模态识别的频率和阻尼比Fig.6 The identified modal frequencies and damping ratios of QCC

表1和表2是根据岸桥的长期监测数据识别出的两种工作状态下1 Hz以内岸桥的固有频率及阻尼比。

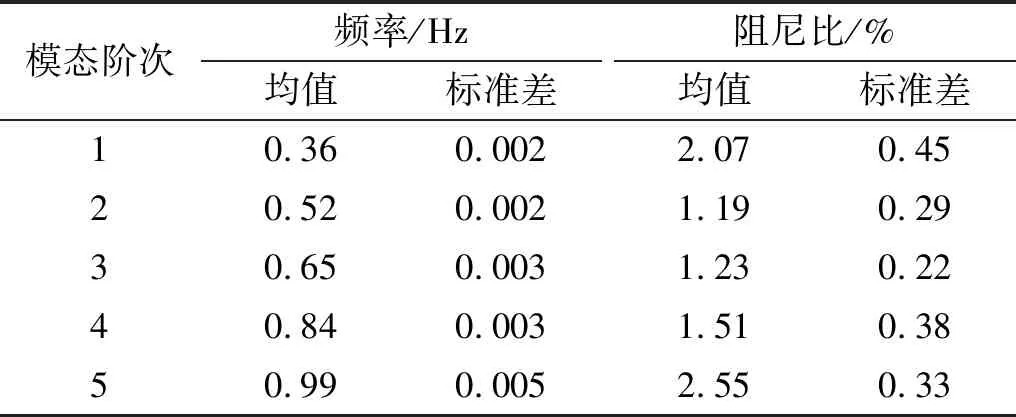
表1 非工作状态下岸桥模态参数识别结果Tab.1 Identified modal parameters under non-working state

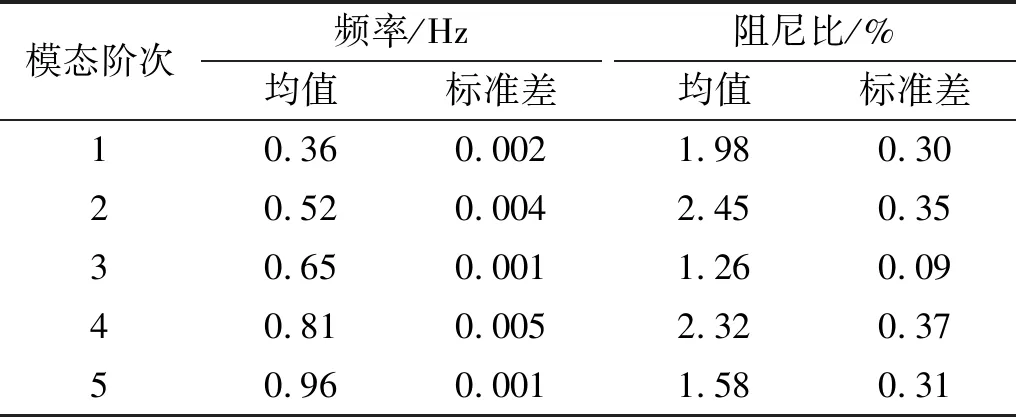
表2 工作状态下岸桥模态参数识别结果Tab.2 Identified modal parameters under working state

本文选取了岸桥处于两种工作状态长度为250 s的监测数据。根据图3与图4给出的数据时程曲线可以看出所取的实测数据稳定，无畸变值，数据的品质较好。根据表1和表2可知，非工作状态下识别的岸桥在1 Hz以内的五阶固有频率分别为0.36 Hz、0.52 Hz、0.65 Hz、0.84 Hz和0.99 Hz，阻尼比分别为2.07%、1.19%、1.23%、1.51%和2.55%。工作状态下识别的岸桥在1 Hz以内的五阶固有频率分别为0.36 Hz、0.52 Hz、0.65 Hz、0.81 Hz和0.96 Hz，阻尼比分别为1.98%、2.45%、1.26%、2.32%和1.58%。

由表1和表2可知，对于两种工作状态识别的频率的标准差值小于0.005，小于相应模态频率均值的0.5%；识别的阻尼比的标准差值小于0.45，小于相应模态阻尼比均值的26%。

由表1和表2两种工作状态下的前三阶固有频率可以看出是对应相等的，当将前三阶固有频率精确到千分位后发现，岸桥非工作状态下识别得到的前三阶固有频率分别为0.359 Hz、0.518 Hz、0.654 Hz；而处于工作状态下的岸桥识别得到的前三阶固有频率分别为0.361 Hz、0.515 Hz、0.653 Hz，可以看出两者的误差最大仅为0.003 Hz。由此可以看出，不同的工作状态对岸桥的前三阶固有频率影响较小，因为，岸桥的前三阶固有频率所对应的振型是在XZ平面内，该平面不是岸桥的工作平面，即非工作平面内的振型，因此，虽然小车(吊重)增加了岸桥整体系统的质量，但这并不会影响非工作平面内的模态结果；相反的，非工作状态下识别得到的岸桥第四阶和第五阶固有频率则明显大于工作状态下识别得到的第四阶和第五阶的固有频率，因为岸桥的第四阶和第五阶固有频率所对应的振型是在XY平面内(Y方向)的振型，该平面为岸桥的起升工作平面，因而，当岸桥处于工作状态时，小车(吊重)会使得岸桥系统整体质量的增加，使得工作平面内模态的固有频率较非工作状态有所下降。由此可见，不同的工作状态对岸桥工作平面内的模态结果会产生较大的影响，而对于非工作平面内的模态结果，不同的工作状态的影响程度则较小。

为了进一步说明岸桥不同工况对岸桥频率的影响，本文通过建立相应的有限元模型(按照工程图纸)，在前大梁小车运行行程(约69 m)上等距选取16个点将小车(吊重)简化为集中质量分别放置于该16个位置模拟小车(吊重)在岸桥前大梁上的运行工况并进行模态分析，模拟分析得到了相应模态下的岸桥的前五阶固有频率，图7中实线为前五阶固有频率，虚线为频率的均值线。通过图7可以明显看到，当岸桥处于工作状态时，前三阶固有频率几乎不发生变化，而第四阶和第五阶固有频率则出现了下降(该两阶频率对应的振型为工作平面内的振型)，可见，小车(吊重)会对岸桥工作平面内的模态结果造成影响而对非工作平面的模态结果几乎不产生影响。

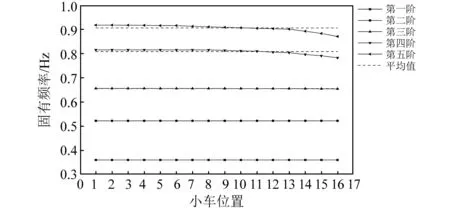
图7 工作状态岸桥的有限元模态分析结果Fig.7 The modal results of QCC under working state by FEM

图8为岸桥处于非工作状态以及工作状态下的识别得到的振型结果。考虑到安全原因，未在岸桥的前大梁布置传感器，因此在保证测点的识别振型与有限元对应位置振型的MAC值在90%以上的条件下参考有限元前大梁的振型。图8中，虚线对应于岸桥处于静平衡位置，实线为工作状态下识别得到的振型，双点划线为非工作状态下识别得到的振型。

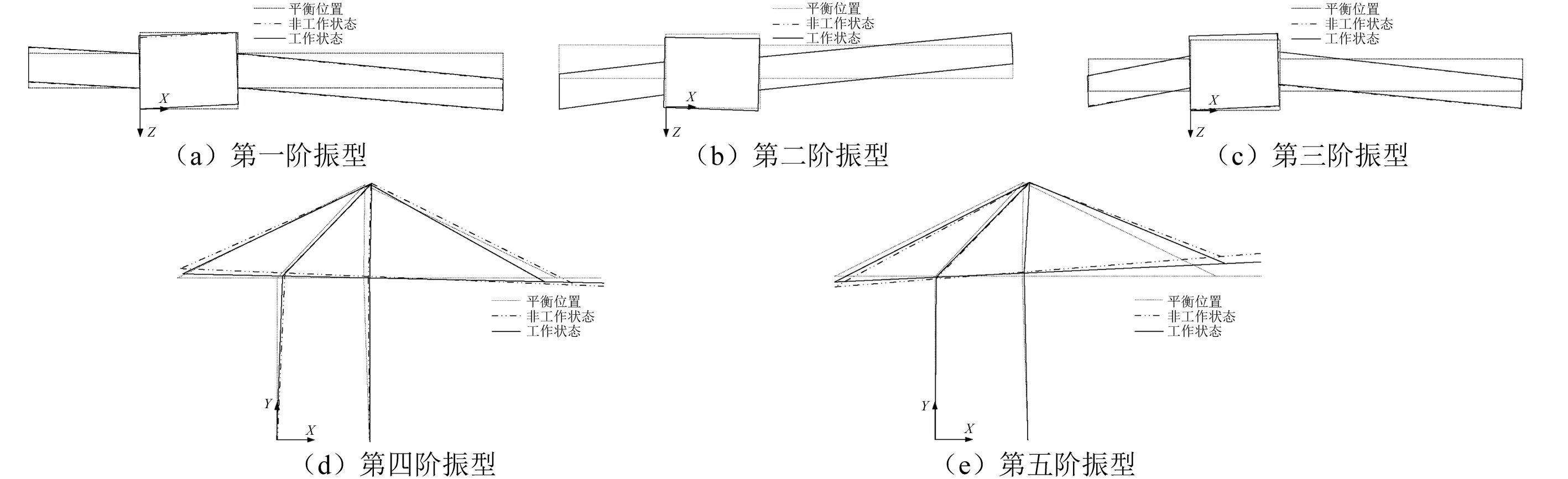
图8 两种工作状态下岸桥的模态振型识别结果Fig.8 Identified mode shapes of QCC under different working state

根据表1、表2以及图8可以发现，对于本文的监测岸桥，前三阶振型为大车行走方向(Z方向)的振型，该平面为岸桥的非工作平面，其刚度较小，因此首先出现该平面内的振型；后两阶振型为竖直方向(Y方向)振型，该平面为岸桥的起升工作平面，其设计刚度较大，这也与实际工程经验相符。

图8表明，两种工作状态下的岸桥的前三阶振型非常相似，计算两种工作状态下识别的前三阶振型之间的MAC值可以发现，前三阶模态振型的MAC值在93%～97%之间，而岸桥的第四阶和第五阶振型存在一定的差异，这是因为小车(吊重)对岸桥起升工作平面的振型产生了一定的影响，而对非工作平面的振型产生的影响较小。可见，小车(吊重)质量的影响不仅体现在对岸桥的固有频率上，同时，对岸桥的振型也存在类似的影响。

3 结论