针对机器人柔性负载振动控制的输入整形技术实现方法

李 琳， 胡锡钦， 邹焱飚

(华南理工大学 机械与汽车工程学院，广州 510641)

`

工业机器人被广泛的应用在自动化生产领域，如喷涂、搬运、焊接等，由于生产效率和质量的要求，实现高速高精度的运动变得尤为重要。然而，由于机器人柔性结构的影响，高速运行情况下往往会使得机器人产生较大的残余振动[1]，此外，由于末端执行器和负载部件的柔性，即使在较低速度运行时负载部件也会产生振动，比如液体搬运机器人[2]、固晶专用机器人[3]等。残余振动的存在不仅影响定位精度，还使得机器人必须等待振动消除或衰减到允许范围内之后才能继续进行下一步生产工序。为了提高生产效率和生产质量，必须实现快速有效的抑振，也就需要充分考虑机器人系统柔性元素的影响。

在生产中机器人操纵柔性部件是很常见的任务，针对机器人末端柔性负载的残余振动问题，研究者们已提出许多控制方法，比如，基于全部实验数据对柔性臂进行自回归随机建模后设计比例-微分反馈控制律[4]；模糊控制策略[5]；对变形体进行动力学解耦后，采用滑模变结构控制技术实现快速抑制[6]等。闭环控制技术通常需要实时的测量系统的振动，当机器人工作时传感器不得不一直贴在所测系统上。然而，末端柔性负载往往是待加工的部件，不便于安装传感器，所以闭环控制技术难以应用于实际生产中。相比而言，开环控制技术不需要反馈量，免去了传感器安装的不便。Singer等[7]所提出的输入整形技术能有效的抑制柔性系统的振动，并且已经在许多实例中得到了验证。国内许多学者也对此进行了深入研究，赵志刚等[8]提出基于改进型负输入整形和最优控制结合的方法来抑制单关节机械臂的残余振动；董明晓等[9]针对小阻尼单模态振动机采用比例-微分结合输入整形控制技术消除系统的残余振动；朱春艳等[10]针对太阳翼调姿过程中的残余振动问题，提出零位移输入整形前馈控制方法。上述研究主要是基于单自由度系统，而单自由度操作器并不是真正意义上的机器人，相比而言多自由度机器人末端执行器的运动形式较为复杂，比如平移、旋转或者两者都有，而且不同的运动形式直接影响着柔性臂的振动[11]。

通常来说，对于多自由度的工业机器人很自然的会想到对各关节分别实行输入整形，但是由于输入整形技术自身的一些特性使得关节空间整形时将会产生某些副作用，本文将在第二部分分析这些缺点。本文的研究目的在于快速有效的识别模态参数后采用一种无轮廓误差的输入整形技术来控制机器人末端柔性负载的残余振动。

1 输入整形技术

输入整形技术是一种前馈滤波技术，常用来抑制柔性结构点到点运动时产生的残余振动，其控制结构如图1所示。

图1 输入整形结构图
Fig.1 Structure of input shaping

以二阶线性系统为例：

(1)

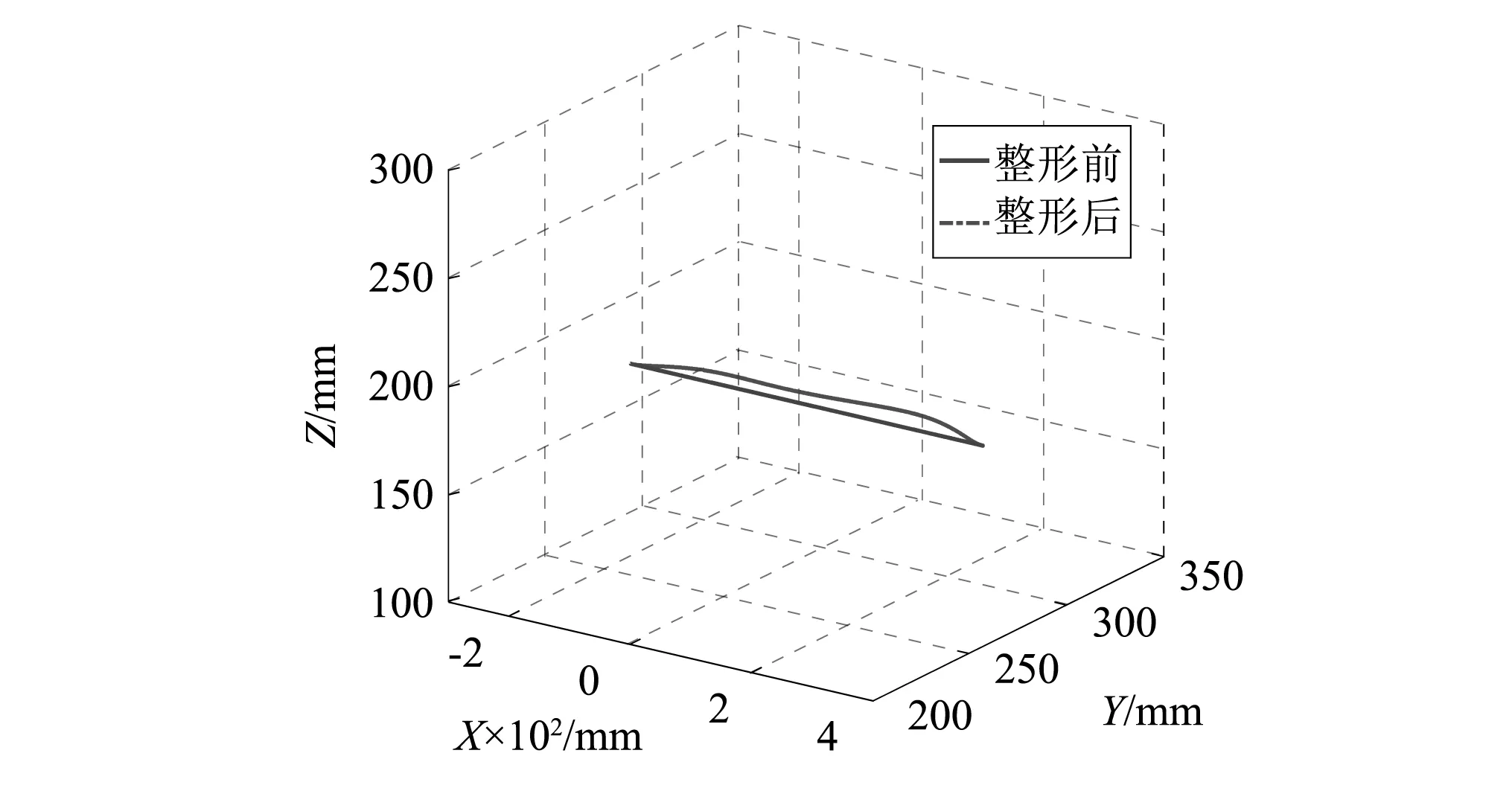
式中:ωn为自然频率;ξ为阻尼比;A为增益。

当输入信号为单位脉冲u(t)=δ(t)时响应为：

(2)

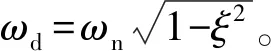
fIS(t)=A1δ(t-t1)+A2δ(t-t2)。

对单位脉冲输入信号整形后得到：

uIS(t)=u(t)*fIS(t)=A1δ(t-t1)+A2δ(t-t2)，

当t≥t2时，由整形输入信号uIS(t)引起的输出响应yIS(t)=0，其基本原理可以由图2来描述。

图2 输入整形原理Fig.2 Input shaping principle

2 关节空间整形的缺陷

对于6自由度机器人系统来说，非常自然的会想到在关节空间中对各个伺服电机的输入信号进行整形来实现输入整形技术。但是由于笛卡尔空间和关节空间之间的映射是非线性的，当笛卡尔空间中按点到点运动时，关节空间中各关节往往会出现往复运动。由于整形器自身的特性，当关节在某一较短的周期内存在往复运动时，对运动指令整形后将产生较大的变形，甚至导致运行轨迹不平滑。

如图3所示，当往复运动的时长与整形器时长接近时，关节空间轨迹进行整形后将出现下述缺点：①整形后的轨迹已经严重变形，轨迹变得不光滑；②无法到达负向(或正向)的最大值，会造成较大的轮廓误差。

图3 对往复运动进行输入整形Fig.3 Input shaping for reciprocating motion

3 笛卡尔空间整形

实际生产应用中，执行点到点运动时笛卡尔空间中的轨迹是单调的，在笛卡尔空间中对轨迹进行整形则可避免出现上述关节空间整形的缺点。同时，对于存在球形手腕的6自由度工业机器人，其运动可拆分为手腕位置的平移运动和姿态的旋转运动。而柔性臂的振动与机器人末端的运动直接相关，在加速和减速过程中，柔性臂受外力激发而振动[12]，柔性体的振动方程为：

(3)

式中：u为质点的位移;M为质量矩阵，C为阻尼矩阵;K为刚度矩阵；F(t)为外部激励与机器人末端的运动和柔性板自身重力有关。当机器人末端的运动方向与柔性臂的变形方向平行时，柔性体的振动最为明显，主要分为两种情况：①运动方向与重力方向垂直；② 运动方向与重力方向平行。为保持柔性板的变形方向与机器人末端的移动方向一致，分解为平移运动和旋转运动更有利于柔性臂的控制，然后分别对位置轨迹和姿态轨迹进行整形即可实现笛卡尔空间中的输入整形。

3.1 机器人位置规划

首先定义轮廓误差为：滤波后轨迹与原始设计轨迹之间的误差[13]。同定位精度一样，轮廓误差是机器人应用中另一需要重点考虑的问题，由于机器人末端的运动是由六个关节相互耦合的结果，当对各关节的轨迹分别整形后，则会造成末端执行器偏离设计轨迹，即出现轮廓误差，如图4所示。

(a) 关节空间轨迹

(b) 笛卡尔空间轨迹 图4 输入整形前后轨迹对比Fig.4 Trajectory contrast with/without shaping

为了消除整形引起的轨迹轮廓误差，本文采用一种沿轨迹方向的整形方法，假设笛卡尔空间中轨迹为[x(t),y(t),z(t)]，取参数：

(4)

式中：S(t)代表沿轨迹方向的长度，笛卡尔空间轨迹的坐标可按参数S(t)重新定义为[x(s),y(s),z(s)]，只需对S(t)进行整形，再计算出对应的笛卡尔坐标即可实现机器人手腕平移运动的整形。而此方法实际表现为沿轨迹方向重新配置速度，理论上整形后不存在轮廓误差。下面以圆弧轨迹为例进行说明，对于空间中一条圆弧轨迹，先以圆心为原点建立坐标系oxyz，使圆弧处于xoy面内，以便于将圆弧参数化，如图5所示。

图5 圆弧轨迹的表示方法Fig.5 Description of the arc trajectory

在坐标系oxyz下，圆弧可以表示为：

(5)

则

(6)

式中：半径r为常数，θ(0)=0，则输入整形的实现步骤为：

步骤1 对S(t)进行输入整形得到

SIS(t)=S(t)*fIS(t)；

步骤2 计算相应的[x(sIS),y(sIS),z(sIS)]；

步骤3 通过旋转变换矩阵将[x(sIS),y(sIS),z(sIS)]换算至基座标系OXYZ中。

步骤4 通过逆运动学计算各关节的运动指令。

3.2 机器人姿态规划

对于姿态运动轨迹的整形，为保证整形后姿态轨迹与位置轨迹的时长相等，同时为避免因姿态规划而引起的振动，使姿态和位置的变换速率保持一致，对姿态轨迹的整形采取下述方法：

(7)

式中：ΔS为位移轨迹总长；Δφ表示欧拉角的变化量。

4 模态参数识别

输入整形器的设计需要预先获取系统的自然频率和阻尼系数，而整形器的效果主要取决于能否准确识别系统的模态参数。对于柔性结构的残余振动，可近似的当成有阻尼简谐振动，本文基于傅里叶频谱分析来识别振动频率，对残余振动信号进行快速傅里叶变换，分析频谱图来获取系统主要的振动频率。阻尼系数则通过对数衰减法来计算[14]，由式(2)可知，振动信号为衰减的正弦信号，其包络线为：

(8)

则取对数之后为一条直线：

(9)

令M=-ξωn，则可得阻尼系数为：

(10)

5 实验及结果

5.1 实验平台

实验平台如图6所示，前述方法将在GSK RB03A1型工业机器人上进行验证，RB03A1机器人有6个旋转关节，并且与著名的PUMA机器人有类似的运动学特征。机器人末端安装有实心的柔性铁板，尺寸为500 mm×100 mm×1 mm；加速度传感器(型号为：kistlerK-Beam8395A，测量范围为：±30 g)贴在柔性板末端用来采集振动信号。控制系统由机器人控制柜和一台标准的计算机组成，其中计算机配置Intel双核3.4 GHz处理器以及4 GBRAM，同时为搭建实时控制系统，采用了一套名为Kithara RealTime Suite的基于Windows的实时拓展软件，在此基础上通过以太总线式通讯方式对机器人的运动进行实时控制，其中采样周期为1 ms。模态参数识别过程及振动信号处理均在MATLAB软件中完成。

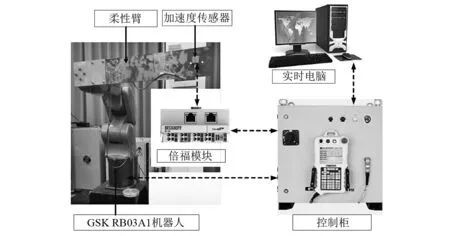
图6 实验装置Fig.6 Experimental setup

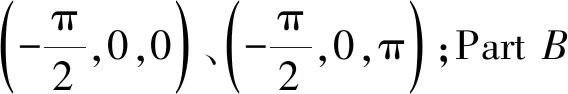
图7 设计的轨迹Fig.7 Designed trajectory

5.2 残余振动信号处理及模态参数识别

为节省篇幅，下面仅以直线轨迹“Part B”运动为例进行说明。首先，机器人按未整形的轨迹运行，然后当运动停止时同步采集柔性板的残余振动，最后对振动信号进行低通滤波滤除噪声，截止频率为50 Hz，如图8所示。

图8 残余振动信号(Part B)Fig.8 Residual vibration of the “Part B” motion

基于傅里叶频谱分析，对残余振动信号进行快速傅里叶变换得到的频谱如图9所示，从频谱可以清楚的获取频率参数，其中按“Part A”轨迹运行时振动频率为3.865 Hz，按“Part B”轨迹运行时振动频率为3.95 Hz。

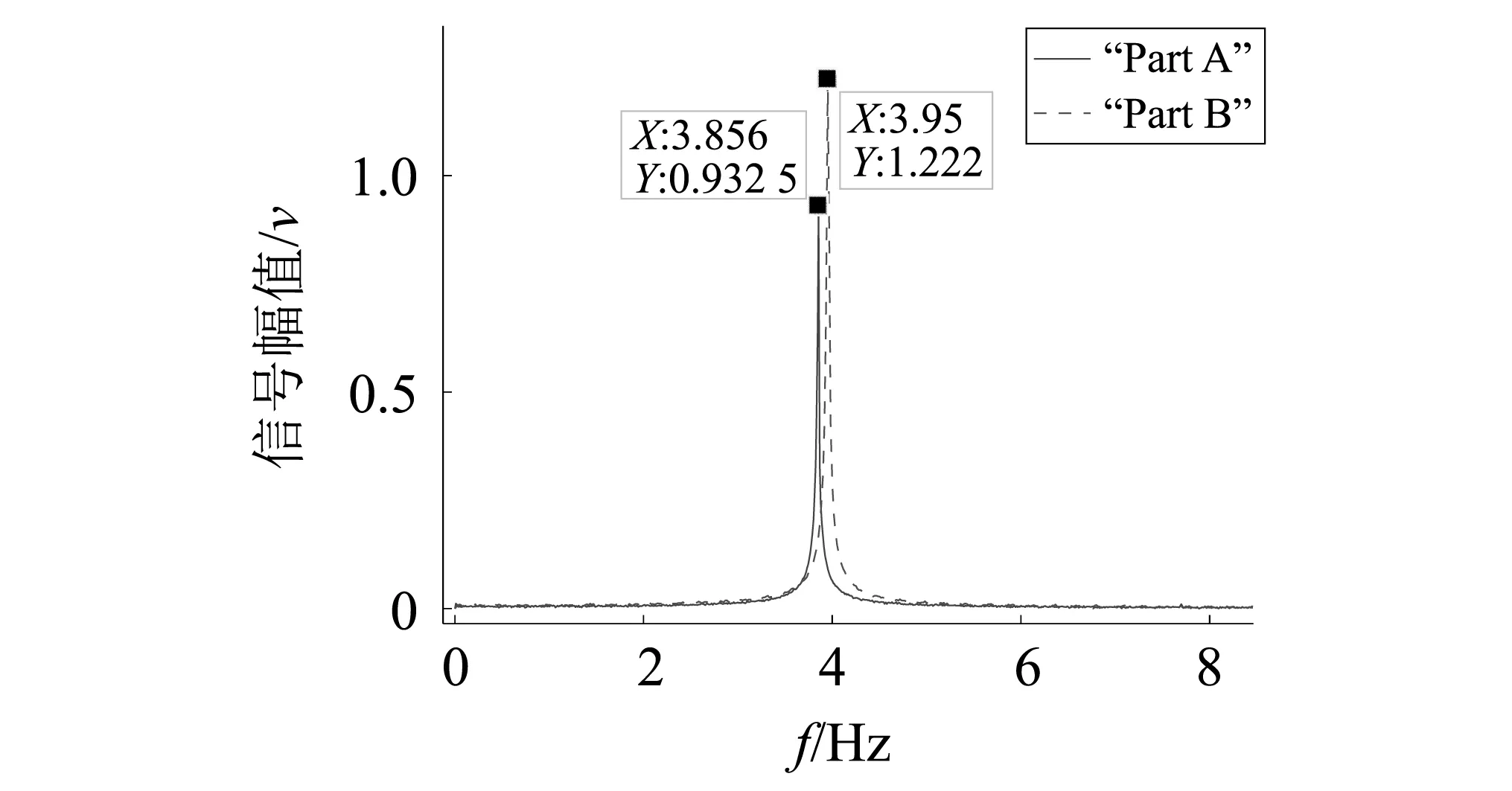
图9 残余振动信号频谱图Fig.9 Power spectrum

在进行阻尼系数识别之前先提取残余振动信号的波峰值如图8所示，根据式(9)，需对峰值z(t)取对数。为了提高准确性，对波峰值取对数后利用最小二乘法拟合(如图10所示)，计算得到拟合直线的斜率即M，根据式(10)则可求得阻尼系数，ξA=0.002 9、ξB=0.003 7。

图10 最小二乘法拟合波峰值Fig.10 Least squares linear method

为验证所识别到的参数的准确度，按简谐振动形式仿真振动信号，如图11所示。

图11 实测信号与仿真信号对比Fig.11 Comparison of the measured and simulation signals

5.3 抑振效果

本文所述的笛卡尔空间整形方法在实验平台上进行了验证，实验中采用两脉冲的ZV整形器，整形器参数，如表1所示。

表1 整形器参数Tab.1 Parameter values of shaper

为了评估所述方法的优点，对比分析了关节空间整形的抑振效果，如图12所示。实验结果表明，关节空间整形和笛卡尔空间整形方法都能减小振动，本文所述笛卡尔空间整形方法更有效地抑制了末端柔性臂的残余振动，从图12中可知，整形前“Part A”和“Part B”运动后残余振动的最大幅值分别为4.7 m/s2和5.9 m/s2；采用关节空间整形方法后残余振动的最大幅值分别为1.2 m/s2和1.8 m/s2；而采用本文所述整形方法后残余振动的最大值均低于0.5 m/s2，相比于整形前振幅衰减约90%，从工程应用的角度来看，可以认为此时机器人已经稳定下来，继续进行生产。

图12 两种方法的抑振效果Fig.12 Experimental results of the two approaches

针对轮廓误差的问题，对比分析关节空间整形和本文所述笛卡尔空间整形方法，误差如图13所示，采用本文所述方法所产生的轻微误差是由于输入信号数字化过程中采用圆整处理以及后续数值计算所致，而关节空间整形时不可避免的出现轮廓误差，且图中“Part B”运动中误差值高达9 mm主要是由于某一短周期内关节空间中轨迹存在往复运动，实施整形技术后造成轨迹失真。

图13 轮廓误差Fig.13 Contour errors of the two approaches

6 结 论

本文针对由机器人操纵的柔性臂自由端的振动问题，提出了一种无轮廓误差的输入整形方法，该方法的主要特点和效果如下：采用了一种基于傅里叶频谱分析和时域分析的模态参数识别算法，仿真结果证明该算法能准确地估计系统的振动频率和阻尼系数，从而保证设计的整形器合理有效；基于运动轨迹参数方程的整形方法，实际为沿轨迹方向对速度进行重新配置，从理论上消除了轮廓误差。为验证所述方法的有效性，搭建了机器人-柔性臂实验平台，实验结果显示柔性臂自由端振幅衰减高达90%，说明该方法有效地抑制了残余振动；相比于关节空间整形引起的较为严重的轮廓误差，该方法消除了轮廓误差，这对实现高精度的运动是十分有益的。