起伏振动状态下水平管内气液两相流研究

周云龙， 常 赫， 赵 盘

(东北电力大学 能源与动力工程学院，吉林 吉林 132012)

近年来随着科学技术向水下潜艇、漂浮式核能设备以及航天领域的深入研究，国内外关于动态条件下管道内流动特性的研究正在逐步开展[1-4]。受海洋等自然条件的影响，设备元件会发生倾斜、摇摆、起伏振动、水平振动等情况，这些附加运动会影响气液两相流动状态，相应也会影响设备的寿命和安全运行[5-6]。相反，充分利用振动也能强化传热[7-8]。

目前，关于摇摆与倾斜状态下管内两相流动方面的研究已有明显的成效，如摇摆引起的附加惯性力可以改变管内气液两相流型及摩擦阻力[9-11]。工程应用中，李金辉等[12]通过研究液体晃动对槽罐车前轮摆振系统的影响，提出了减小槽罐车摆振的措施。与之相比，对于气液两相流流经振动状态下管道的研究则鲜有报道。而在一些实际工程中如道路施工时地下管道的振动以及海底管道油气的运输，其动力运输装置均会发生振动，相应影响了气液两相流动情况。由此可见，动态条件下管道内气液两相流动情况有很大研究价值。

现有研究表明气液两相在振动通道内的流动情况与稳态下有一定差异。Pendyala等[13-14]研究了低频振动下垂直通道内气液两相流动，得出振动增大了两相流速以及压降的结论，同时发现在层流领域内，振动可以增大传热系数。Chen等[15]通过对低频振动下气水两相进行实验研究，发现流动结构和界面浓度发生了明显改变。然而，国内外学者对于振动情况下流型及流型转变界限的研究尚未得出统一的结论。

随着计算机技术的发展，数值模拟作为一种重要手段广泛应用于各类研究中。由于气液两相界面密度及压力等存在巨大差异，关于气液两相流的数值模拟一直是流动模拟的热点，其研究重点是运动界面的追踪以及边界条件的构造[16]。由于通道结构与流体间流固耦合作用的复杂性，对于振动通道内气液两相流动的数值模拟则是少之又少。

基于上述原因，本文依据工程实例中车辆颠簸行驶引起管道产生的高频低幅式振动以及船舶航行时所引起的低频高幅式振动等因素，通过实验的方法研究了起伏振动状态下气液两相流型及流型转换界限。同时，利用FLUENT软件模拟了各种不同振动状态下管道内流体流动情况，对比了不同工况下流型转换界限的差异性，为后续动态条件下管内传热以及两相流动的数学模型奠定了基础，以期对振动状态下设备管道的安全运行起到一定的指导作用。

1 实验装置及原理

本实验在两相流实验回路基础上与振动装置相连接，如图1所示。实验段直径为35 mm的有机玻璃管，且水平固定于振动台上，振动装置如图2所示，实验段与振动装置同步做水平正弦运动。实验原理参考文献[17]。

图1 实验系统流程图Fig.1 Schematic diagram of experimental apparatus

图2 振动装置示意图Fig.2 Vibration experimental apparatus

2 数值计算

2.1 物理模型及网格划分

本文依照实验数据使用PRO.E进行几何造型，进口管径r0为27 mm，壁厚w0为5 mm，通道直径r1为35 mm，管长L为2 m。利用ICEM进行网格划分，对通道壁面附近网格进行边界层细化处理，然后将网格导入ANSYS FLUENT 15.0进行三维计算。模拟工况之前，对网格进行无关性验证，研究发现网格数对壁面压力几乎没有影响，与Lim等[18]得出的结论一致。因此，通过比较不同网格划分时稳态工况下通道内弹状流的气泡长度，最终确定本文采用网格数为396 000的非结构化四面体网格进行计算。几何模型及网格分布，如图3所示。

图3 几何模型及网格划分Fig.3 Geometric model and mesh geometry

2.2 控制方程及边界条件

本文基于FLUENT平台，采用CLSVOF模型进行计算追踪流体界面变化情况，其控制方程及边界条件设置详见参考文献[19]。同时利用UDF编程手段，在动网格模型下实现起伏振动工况下的模拟。每次模拟过程中，为保证收敛，需适当调整时间步长和松弛因子。在动网格模型中，任一控制体V内，其边界是运动的，动量方程[20]为：

(1)

式中:vx和vy分别为控制体沿x轴及y轴方向的运动速度，m/s;a为控制体加速度，m/s；f为作用在单位质量流体上的质量力，N。

3 结果与讨论

3.1 实验结果及模型验证

管内气液两相流动情况随实验段的起伏振动不断发生变化，借助高速成像系统观察实验段内流体流动情况，可发现振动状态下水平通道内气液两相流型主要有：珠状流、泡弹流、沸腾波状流、波状流以及环状流。

为验证本文所采用数值方法的可靠性，以振幅为5 mm、振动频率为5 Hz的振动工况为例，对数学模型进行验证，其中气相表观速度jG的变化范围为0.015～12 m/s，液相表观速度jL变化范围为0.02～2.5 m/s。计算结果如图4所示，可以发现数值模拟与实验得出

(a) 沸腾波状流(jG=0.14 m/s, jL=1 m/s)

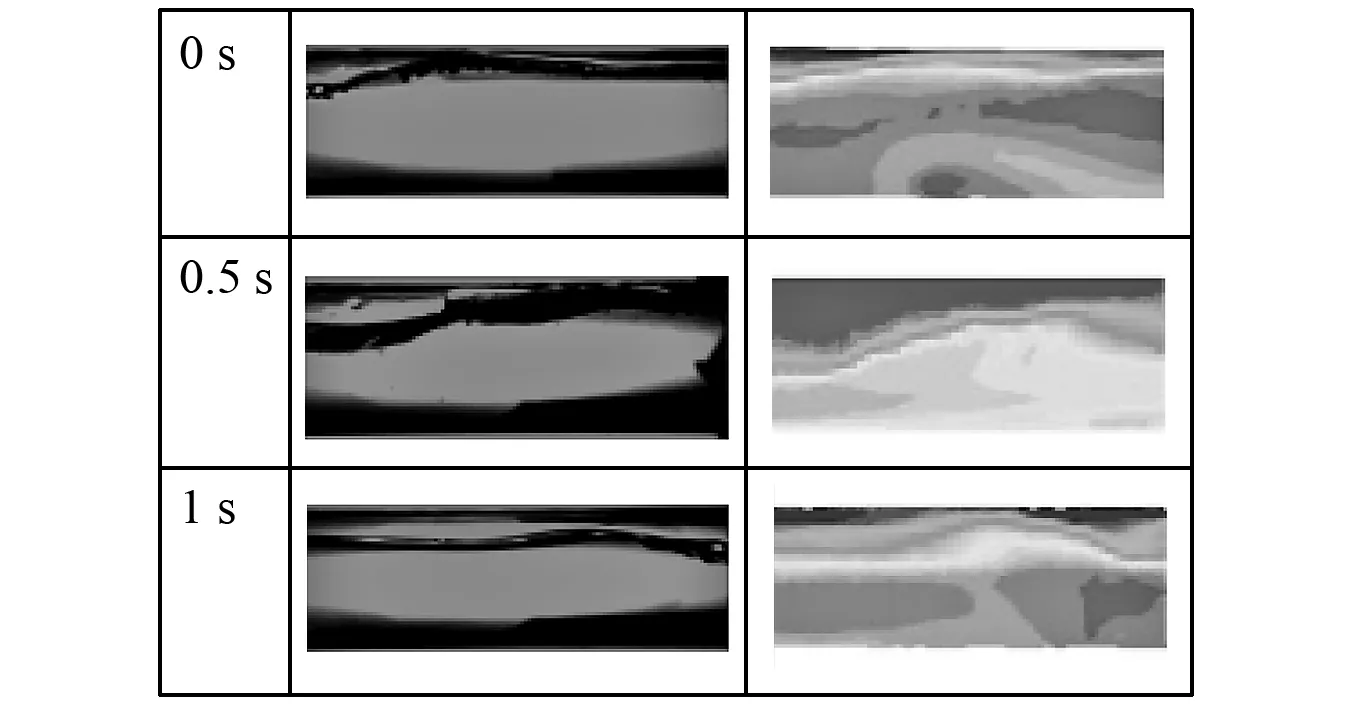
(b)波状流(jG=0.29 m/s, jL=0.2 m/s)

(c)环状流(jG=10.14 m/s, jL=0.1 m/s) 图4 实验结果和模拟结果Fig.4 Comparison of flow regime between numerical simulation and experiment

的流型特征基本一致。同时，为定量验证，本文根据大量实验和模拟结果，绘制了如图5所示的流型图。由此可见该方法可以很好的模拟起伏振动工况下管道内气液两相流动情况。

图5 流型转换界限Fig.5 Comparison of transition line

与此同时，当雷诺数逐渐增大时，本文测量与计算了起伏振动状态下气液两相流动的平均压降，结果如图6所示。进一步证明本文所选取的求解算法可以正确反应振动工况下管内气液两相的流动情况。

图6 平均压降结果比较Fig.6 Comparison of mean pressure drop

3.2 振动对压降的影响

Catalina等[21]通过对振动工况下垂直管内气液两相流动进行实验研究，得出压力是流体流动情况改变的关键因素。为此，本文将不同振动状态下管内气液两相流平均压降进行了实验与模拟计算。由于实验的局限性，当振动频率为16 Hz，振幅大于5 mm时，压降值通过模拟给出。结果如图7所示。

图7 不同工况下压降变化Fig.7 Mean pressure drop under different conditions

如图7所示，对比稳态与动态工况下管内气液两相流动压降可看出，振动状态下平均压降值明显高于稳态。同时可看出，压降随振动频率及振幅的增大而增加。但当Re>5 600时，无论是振动频率还是振动幅度对压降均没有很大影响。为探讨振动频率与振动幅度对压降影响的差异性，本文将Re数分为三组进行比对，结果如表1所示。

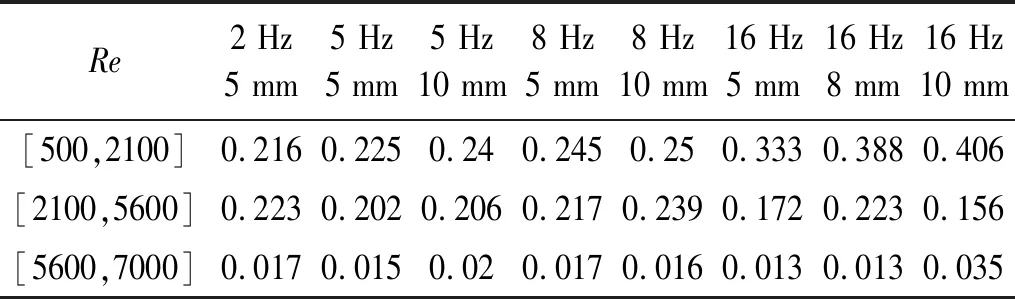
表1 压降变化斜率Tab.1 slope of mean pressure drop

由表1可计算出，当振动频率保持稳定、振动幅度改变时，压降以7.435%的速度增长；当振动幅度保持稳定，振动频率改变时，压降以9.66%的速度增长。由表中数据可发现，高振动频率及振动幅度下，压降变化更快，当雷诺数超过一定范围时，振动几乎不改变压降，与上文所得结论一致。由此可以发现振动频率对气液相流的压降影响更大，分析如下：

在静止稳定状态下，影响压降的主要因素包括Re数和通道壁面性质等，而Re数又受到通道几何结构、流体速度及流体性质等。对于起伏振动工况下的管内两相流动，还需考虑振动的变化所引起通道做正弦运动时加速度的变化，从而导致通道内两相流体所受到的附加力发生改变，进而影响压降。同时，流体的对流效应受振动频率、振动幅度、流体黏度等参数的影响。当通道做起伏振动时，在通道壁面很薄的区域内会产生瞬时脉动涡流，同时产生巨大的脉冲速度，由于这一区域内的非线性作用，这些脉动涡流在边界层内引起的振幅传递到流体内部，进而影响流场结构，振幅和频率的增加均使得通道内压降迅速增大。振动幅度和振动频率越大，对原有流场结构影响越大，致使流动更加紊乱，流线偏离原方向的程度也越大。小振幅低振动频率时，大尺度旋涡变成小尺度旋涡，进而发生破碎，随主流流动；大振幅高频率时，大尺度旋涡也发生破碎，流入主流。因此，高频率和高振幅下压降变化更加明显。然而随着气液流速的增大，惯性力逐渐削弱振动所带来的影响，压降随之稳定。

3.3 黏度对流型及压降的影响

由上文可知，通道内气液两相分布情况不仅与外部因素有关，流体性质也会对压降及Re数产生一定的影响。因此，为探讨黏度对流动情况产生的影响，该部分采用三种不同质量分数的甘油作为液相，其物性参数见表2。当甘油溶液质量分数增大时，其表面张力及密度变化很小，可近似认为恒定，但黏度变化相对较大，因而本文采用该种溶液来衡量液相黏度对振动状态下管内气液两相流型及压降的变化。压降变化规律和流型转换界限分别如图8和图9所示。

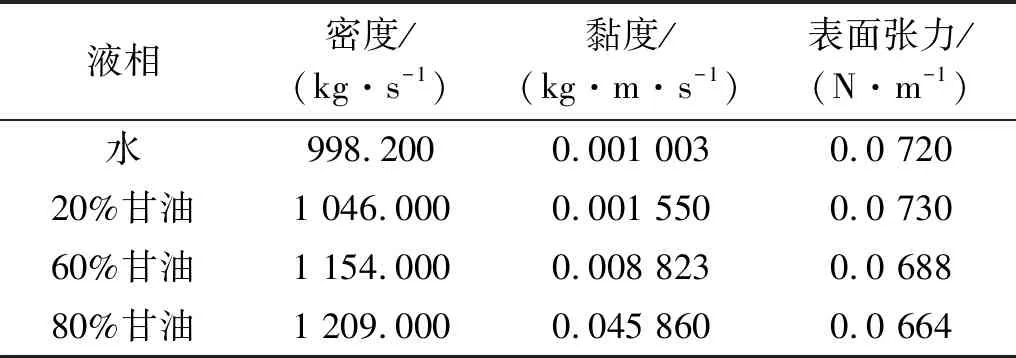
表2 液相物性参数(20℃，101.325 kPa)Tab.2 s physical properties of liquid phase

图8 黏度对流体平均压降的影响Fig.8 Comparison of mean pressure drop under different liquid viscosity

如图8所示，振动对气液两相流压降的影响随流体黏度的增大而逐渐削弱。当流体黏度达到0.046时，振动工况下气液两相流压降和稳态工况下大体一致。对此，我们做如下分析：

通道做起伏振动时引起流体的振动强度可通过瑞纳德数衡量，

(2)

流体黏度增大时，流体内部黏滞阻力会变大，气液两相流体微团之间的相对运动会相对困难。由式(2)可看出，当振动频率和振动幅度相同时，振动在高黏度流体中引起的对流效应相对较小，因而削弱了振动对

图9 黏度对流型装换界限的影响Fig.9 Comparison of transition line under different liquid viscosity

压降的影响。这也与Chen等[22]所得出的结论一致，他们发现流体黏度和通道直径可以减小动态工况对于压降的影响。

由图9可以看出，当流体黏度相对较小时，沸腾波状流向波状流转换需要更高的气相速度，波状流向环状流转换相对容易。整体来看，流体黏度对流型转换界限影响不大。这与稳态情况气液两相流型转换变化趋势大体一致。

周期性起伏振动情况下，流体中的速度可分为平动速度和脉动速度。流体流动速度随流体黏度的增加而减小，当流体黏度较小时，流体速度随黏度增大下降较快；而当流体处于高黏度状态时，流体速度随黏度增大缓慢下降。气液两相在通道内流动过程中，表面张力影响珠状流的形成，惯性力影响环状流的形成[23]。而沸腾波状流和波状流的形成由二者共同作用形成。

F=ρvDh/σ

(3)

式中:F为惯性力;ρ为流体密度；v为流体速度;Dh为通道当量直径;σ为表面张力。与液相黏度关系不大，因而流体黏度对起伏振动工况下通道内气液两相流型转换界限影响不大。

3.4 振动工况对流型转换界限的影响

Gang等[24]通过对起伏振动工况下矩形通道内气泡流动特性进行实验研究得出结论：随振动频率增大，气泡密度以及尺寸等特性随之增大。因此，为探讨振动频率及振动幅度对管内气液两相流动流型转换界限的影响，该部分结合实验方法与模拟计算进行研究，结果如图10和图11所示。

如图10和图11所示，振动工况改变所引起的流型转换界限的变化主要表现在以下几个方面：

(1) 流体具有相同气相折算速度时，振动频率和振动幅度的增大使珠状流转换边界右移。当振动频率为2 Hz时，并未发现珠状流。振动频率以及振动幅度的增加均使管道的起伏振动更加剧烈，从而引起了更大的振动附加力。管内气液两相也会因此产生更强烈的对流作用，气泡间的碰撞更加剧烈，气泡更容易聚合。由于珠状流的形成受液相速度影响，因而需要更大的液相流量产生湍动力维持气泡的存在，即需要更高的液相折算速度，从而增大了沸腾波状流的区域。

(2) 振动频率和振动幅度的增加使沸腾波状流的转换界限上移。振动工况下，管内气液两相流型中沸腾波状流的表现较为稳定，振动工况的改变影响流体流动剧烈程度，基本不发生流型转变。随着管道振动剧烈程度的增加，液相波动程度加剧，下层液相流动对上层气相的扰动增大，气相更容易被分裂，即更易形成沸腾波状流，减小了波状流区域。

(3) 当通道内气液相流速均较大时，振动工况对沸腾波状流及环状流间的转换界限几乎没有影响。如上文所述，当气液相流速较大时，流场所具有能量较大，由于振动能量的输入，进一步迅速增大流场本身能量，等同于振动对流场起到了做功的效果，而这些功则转化为流场自身的能量，从而削弱了振动频率或者振动幅度增大对其产生的影响，保证了流体流动的稳定，从而使得流型转换更加困难。

(4) 振动频率及振动幅度的增大使得环状流的转换界限右移。随振动频率的增大，高速气流周围的液膜波动更加剧烈，液膜稳定性遭到破坏，增加了气相在管道内的流动阻力，形成充分发展的环状流需更大的气相流量，相对减小了环状流区域。同时，当振动幅度增大时，意味着增大了管道在时间段内的平均振动速度以及加速度，不利于液膜在通道内的轴向铺展，对液膜沿管壁稳定流动形成了阻碍，维持环状流的形成则需更大的气相流速。

图10 振动频率对流型转换界限的影响Fig.10 Influence of vibration frequency on flow pattern transition line

图11 振动幅度对流型转换界限的影响Fig.11 Influence of vibration amplitude on flow pattern transition line

整体观察图10和图11可发现，随着振动频率或振动幅度的增大，各流型转换界限均有向外扩张的趋势。相对扩大了沸腾波状流及波状流的区域，环状流区域变化相对较小。振动频率和振动幅度对流型影响近乎相同。同时通过对比图10和图11流型转换界限的疏密程度，可以发现与改变振动频率相比，振动幅度的强弱对流型改变影响更小。

4 结 论

本文通过将实验与数值模拟结合的方式，得出如下结论：

(1) 基于FLUENT平台，利用动网格模型和UDF编程可以实现振动工况下气液两相流动的模拟，为进一步研究传热等问题提供了新的方法和途径。

(2) 常温常压条件下，起伏振动工况下水平管内气液两相流型与稳态时有所不同，主要流型有珠状流、泡弹流、沸腾波状流、波状流以及环状流。

(3) 起伏振动对管内气液两相流动平均压降有很大影响。振动状态下管内平均压降明显高于稳态。当振动频率保持稳定、振动幅度改变时，压降以7.435%的速度增长；当振动幅度保持稳定，振动频率改变时，压降以9.66%的速度增长。振动频率对气液相流的压降影响更大

(4) 改变流体黏度时，振动对气液两相流压降的影响随流体黏度的增大而逐渐削弱。与稳态工况类似，黏度几乎不改变振动工况下的流型转换界限。

(5) 振动工况的改变对流型转换界限有所影响。随振动频率或振动幅度的增大，各流型转换界限均有向外扩张的趋势。振动频率对流型转换界限的影响高于振动幅度。