空调器水平管路内R32流动过程的流型变化规律
张浩,刘璐,詹飞龙,丁国良,刘艳涛,郜哲明
(1-广东美的制冷设备有限公司,广东顺德 528311;2-上海交通大学机械与动力工程学院,上海 200240)
0 引言
R32制冷剂因具有优良的环保性和热物性,在制冷空调系统中得到了广泛的应用[1-3]。开发采用R32工质的空调系统,需要了解其在空调管路中的换热和压降特性[4]。流型对蒸发、冷凝以及压降起着关键的作用,不同流型条件下会呈现出不同的换热和压降特性[5-6]。节流后的气液两相制冷剂在分配器中的分流均匀性也与两相流型密切相关。例如两相工质以环状流或者弥散泡状流形式进入到空调器用分配器中时,将有助于提高两相工质在多流路蒸发器中的分流均匀性,从而提高换热性能。但是如果两相工质以层状流或弹状流形式进入分配器中时,可能引起分流不均而导致换热性能恶化[7]。因此有必要对R32工质在空调管路内的流型特征及流型转化规律进行研究和预测。
两相工质在管路内的流型变化与工质物性和管径密切相关。对于不同工质物性下的流型研究,现有的两相工质流型研究一般是通过实验或模拟的方法来获得水平或竖直管路中的流型图[8-9],如Baker经验流型图[10]、Taitel-Dukler理论流型图[11]以及在此基础上修正后的流型图[12-13]等;这些流型图的适用工质一般为空气-水或者传统制冷剂。而由于R32工质的气液相密度、黏度等物性参数与空气-水或传统制冷剂差异较大[14-15],因此已有的流型图不能用于预测R32的流型变化规律。
对于不同管径下的流型研究,现有的R32流型研究主要集中于管径小于2 mm的微通道管路。LI等[16]研究了R32在管径约为0.6 mm的水平细管道内的冷凝换热特性,实验观察到了塞状流、弹状流、波状流和环状流等流型。JIGE等[17]研究了R32在管径为1~2 mm的水平微细光管内流动沸腾换热特性,结果表明,在不同管径条件下流型图差异较大。由于R32空调系统中的管道直径通常为5 mm,因此现有的针对微通道的R32流型图并不能直接适用于制冷空调管路中的R32流型变化特性,还需要进一步开展相关的研究。
本文分析了空调器5 mm水平管中气液两相R32流动过程,获得气液两相R32的流型变化规律。
1 研究对象及思路
本文的研究对象是制冷空调系统中典型的水平管路内R32工质的两相流型特征。在空调器水平管路中,气相偏向于管顶部聚集,液相偏向于管底部分布。通常水平管中的基本流型可分为4种:分层流、弹状流、环状流和泡状流。具体特征如图1所示,这4种基本流型的形成与管路入口两相制冷剂的流量和干度有关。
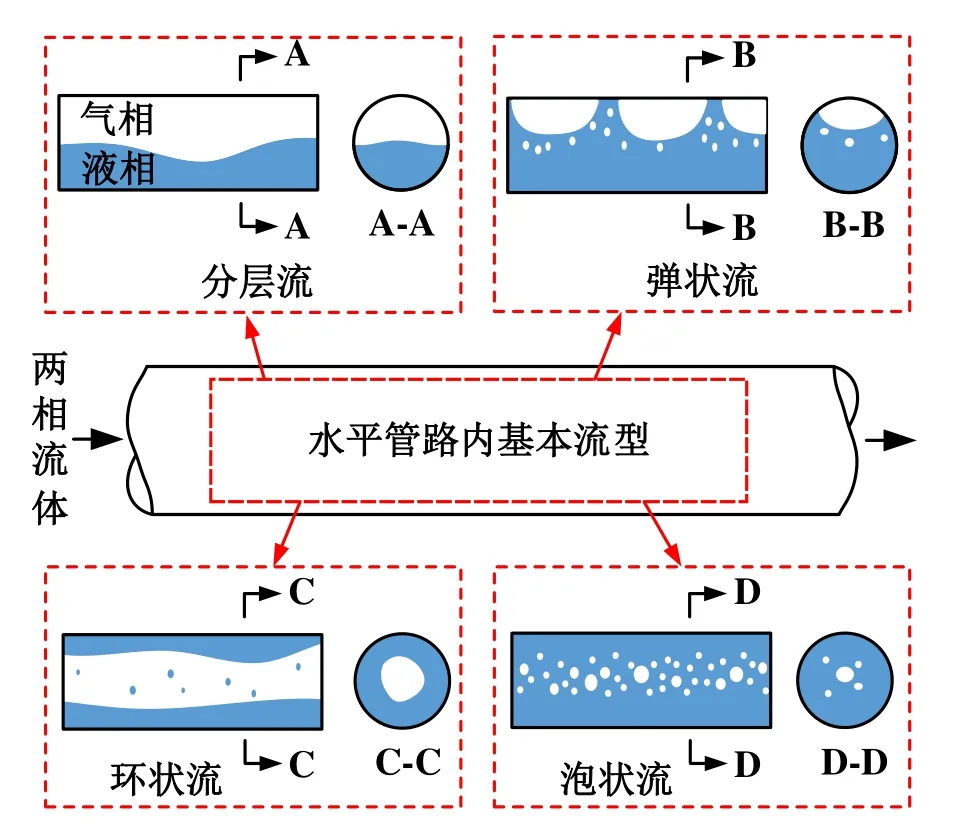
图1 水平管路内两相流型基本特征
本文预测空调系统中水平管路内R32流型转化特征的步骤为:1)开发两相流型模拟方法,基于VOF模型与level set相耦合的方法来描述气液两相的分界面,采用经典水平管内空泡系数模型来计算两相制冷剂的空泡系数,并设置管长大于管径20倍以上来捕捉两相制冷剂充分发展后的流型转变特征;2)预测R32在水平管路中的流型特征。基于该流型模拟方法预测不同气液相表观速度条件下水平管路内R32流型特征并开发流型图。
2 两相流型模拟方法
2.1 气液相基本控制方程
采用多相流流体体积(Volume of Fluid,VOF)模型和level set相耦合的方法对管路中气液两相制冷剂的相界面进行捕捉。应用VOF模型进行两相流模拟计算的基本控制方程组如式(1)~式(3)所示:
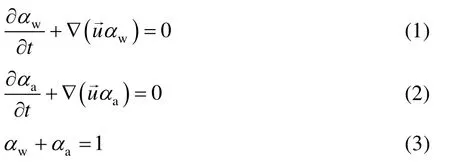
式中,αw为计算单元中液相所占的体积分数,%;αa为计算单元中气相所占的体积分数,%。
VOF方法是通过跟踪管道内所有计算单元中的液相体积分数αw和气相体积分数αa的占比来得到气液相界面的位置。
在对控制方程进行求解的过程中,气液相的物性参数是由计算单元网格上的各相物性参数共同决定,如式(4)和式(5)所示:

式中,ρ、ρw和ρa分别为流体平均密度、液相密度和气相密度,kg/m3;μ、μw和μa分别为流体平均黏度、液相黏度和气相黏度,Pa·s。
由于在整个管道计算域中只求解一套控制方程组,因此求得的速度场和压力场在计算单元中对于液相和气相是各相共享的。
2.2 空泡系数计算模型
为了计算两相制冷剂在水平管路中任一流动截面处气相所占的总面积份额,需要计算两相制冷剂中的空泡系数。可以采用经典水平管内HARMS等[18]建立的模型来计算两相流体的空泡系数:

式中,α为两相流体的空泡系数;Rew为液相流体的雷诺数;x为两相流体的干度;G为两相流体的质量流速,kg/(m2·s);d为管路内径,m;X为两相流体的Lockhart-Martinelli数。
2.3 表面张力模型
计算单元中两相流体动量方程:
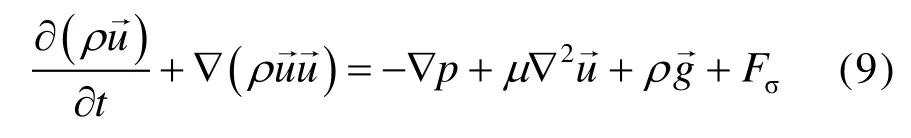
式中,Fσ为两相流体表面张力作用的体积力,N。
Fσ通过连续界面模型给出:
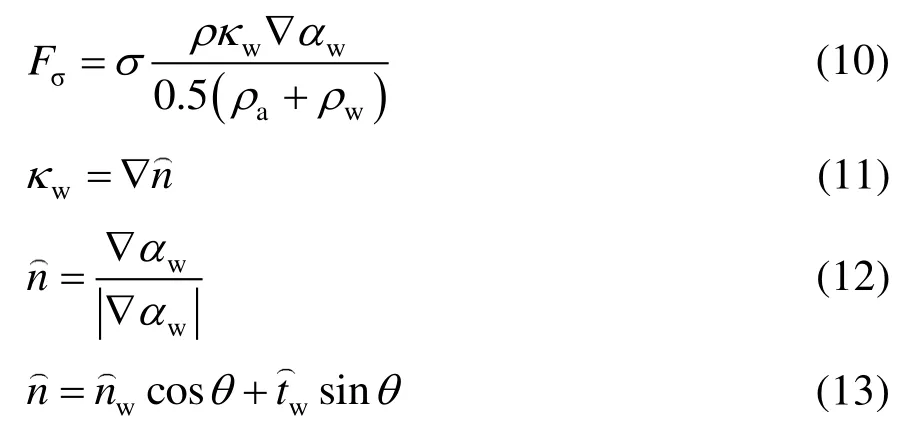
式中,σ为气液相之间的表面张力系数,N/m;κw为相界面的曲率半径,m;为相界面函数;和分别为相界面函数在法向和切向方向上的单位向量;θ为气液相界面与管道壁面形成的接触角,°。
2.4 模拟对象及计算设置
本文基于Fluent软件对水平管路中两相制冷剂流动时的流型变化进行CFD模拟。模拟对象是管内径D为5 mm、管长度L为150 mm的水平管,要求管长度大于20倍的管内径以保证流体在管道内充分发展,如图2所示。
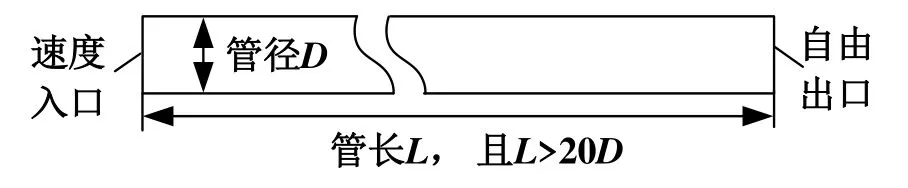
图2 水平管路的模拟对象
模拟计算中采用VOF两相模型和k-ε湍流模型。其中,水平管路入口设置为速度入口,出口设置为自由出口。压力和速度的耦合采用PISO算法,压力项采用PRESTO!格式,动量方程采用二阶迎风格式,气液相界面的处理采用几何重构方案。
对模拟中的网格无关性进行验证。对于边界层网格,取第一层边界层网格大小为0.001 mm,网格层数为6,网格生长率为1.2,可充分反映管壁的流型变化。对于流场网格,依次选取0.20、0.10、0.06和0.04 mm这4种网格大小来计算水平管路中的平均Darcy摩擦因子;可知当流场网格大小由0.06 mm降为0.04 mm时,平均Darcy摩擦因子的变化幅度小于1%,故选取流场网格大小为0.06 mm。
2.5 入口气液相表观速度的模拟工况
入口处按照气液均相入口来分别设置各自的表观速度,计算方法如式(14)~式(15)所示:

式中,ua为气相表观速度,m/s;uw为液相表观速度,m/s。
对于水平管路入口的气液两相表观速度取值范围的选取,参照实际空调器运行中的真实两相制冷剂的质量流量范围和干度范围并利用式(14)~式(15)来计算得到。本文选取的水平管路中两相制冷剂入口质量流量范围为10~110 kg/h,干度范围为0~0.7。根据流型转化的特点,选取对数坐标绘制流型图,在0.01~20 m/s等对数距离选取8个气相表观流速作为横坐标点,在0.001~5 m/s等对数距离选取8个液体表观流速作为纵坐标点。
模拟过程中的假设条件如下:1)流动不可压;2)忽略传热过程,且制冷剂不发生相变;3)制冷剂气相和液相物性参数为常数。
为了加快模拟过程中的流型形成,在计算初始时刻定义整个水平管路内被液相充满,时间步长设定为10-5s以充分保证计算收敛。
3 模拟结果的实验对照
表1所示为在不同入口两相制冷剂质量流量和干度条件下,水平管中充分发展后的流型模拟结果与现有文献中相应流型图的对比。
由表1可知,模拟得到的分层流型、弹状流型、环状流型和泡状流型与文献中相应流型的实验照片吻合度较好。分层流型模拟结果与实验结果之间的差异性主要表现在气液分界面的形态,模拟结果表现为波纹形态,而实验结果中的波纹形态不明显。弹状流型模拟结果中,气弹占据了整个管道截面,而在实验结果中气弹在重力作用下聚集在管道顶部,气弹下方还存在液膜。
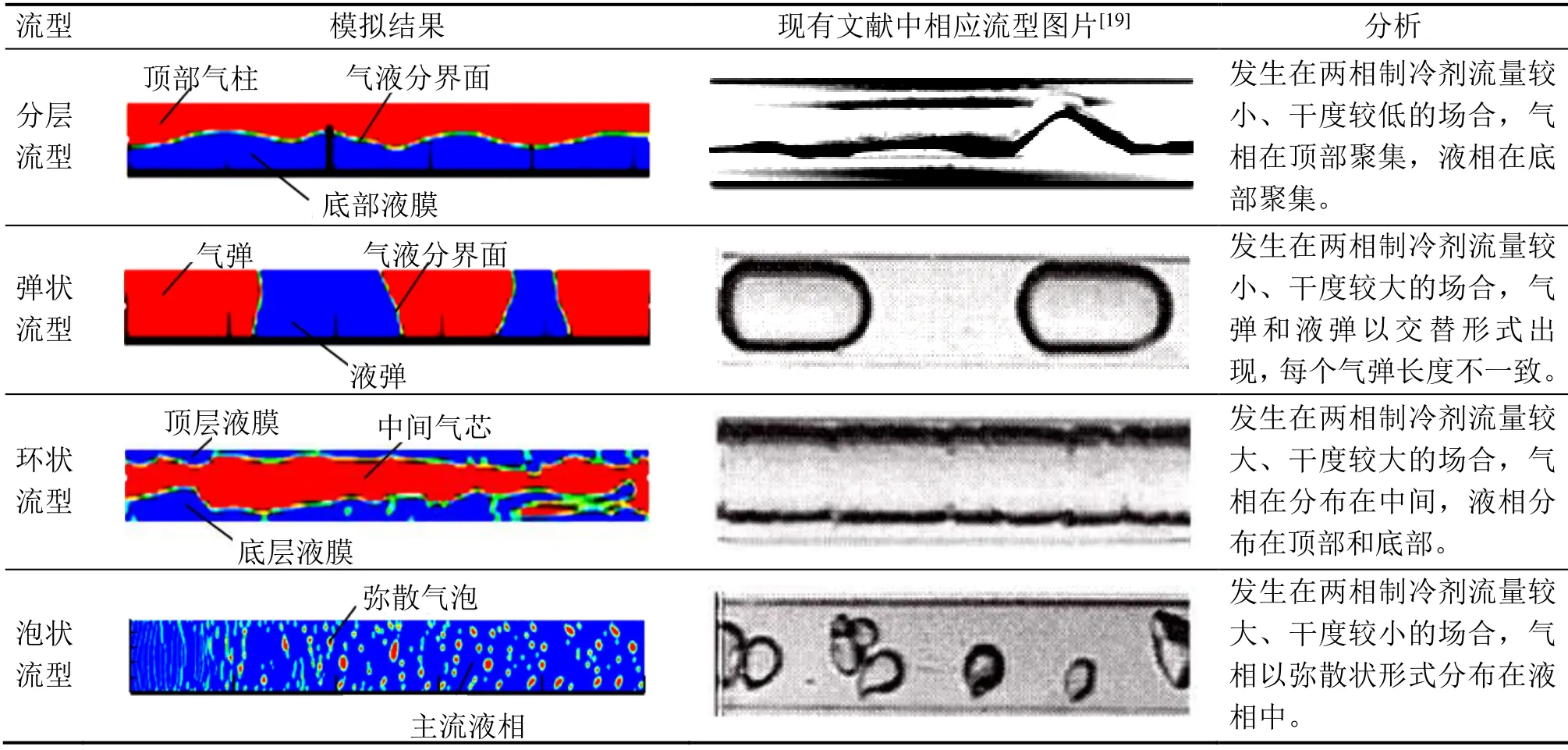
表1 充分发展后流型模拟结果与现有文献中相应流型的对比
4 流型变化规律的模拟分析
4.1 不同时刻R32流型特征的变化
表2所示为在水平管中R32气液两相不同表观速度入口条件下,R32流型特征的变化情况。由表2可知,当入口气液相表观速度均较低时,水平管内R32两相流型将最终发展为分层流型。此时重力使两相完全分离,两相界面光滑,低密度气相聚集在管顶部,液相分布在管底部;当液位达到一定程度时,两相分界面上由于Kelvin-Helmhoz现象[20]还会出现界面波,呈现出波纹层状流的特征。
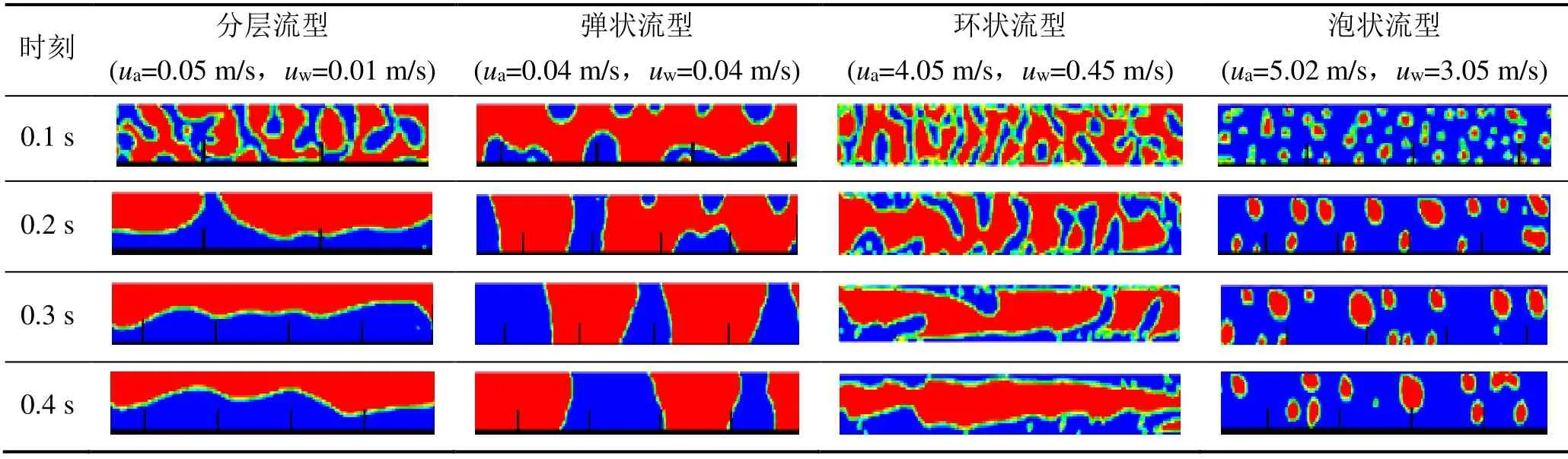
表2 水平管路中不同时刻R32流型变化
随着入口液相表观速度进一步提高,水平管内R32两相流型将由分层流型发展为弹状流型。此时分层流开始不稳定,气液相界面很难保持稳定,在水平管入口处形成扰动,受到扰动的液面碰到管顶部时会形成液弹,从而间歇性地堵塞管道。
随着入口气相表观速度进一步提高,水平管内R32两相流型将由分层流型发展为环状流型。此时液相只能瞬间与管道顶部和底部接触并形成液膜,不能形成连续的液弹。气相则以气柱的形式分布在管道中心,且由于气柱喷射时产生的扰动作用,管道顶部和底部气液相界面的形态也呈现出不稳定的波动形态。且由于重力的作用,液膜在管底部较厚,在气芯中也常携带有一定量的细小液滴。
随着气相和液相表观速度的同步提高,水平管内R32两相流型将由分层流型发展为泡状流型。此时气弹或气柱被液相冲击而破碎成弥散状的气泡群,气泡群在流动过程中会发生小气泡合并成大气泡的现象;形成的大气泡在重力作用下逐渐往管壁顶部移动,并在液相黏滞力的作用下被拉长,从而在管壁某些位置上形成贴壁长泡状流。
4.2 水平管中R32流型
将水平管中R32气液两相制冷剂流型模拟结果,绘制成横纵坐标分别为气相表观速度和液相表观速度的流型图,如图3所示。
由图3可知,水平管中R32分层流型主要发生在液相表观速度较低的条件下,此时液相在管底部堆积现象明显;随着液相表观速度的增加,液相与管顶部直接接触,表面张力的作用克服重力使得分层流型逐渐向弹状流型转化;而随着液相表观速度进一步提高,弹状流型会继续向泡状流型转化;在分层流、弹状流或泡状流型中,随着气相表观速度的提高,各自的流型均有可能向环状流转化。
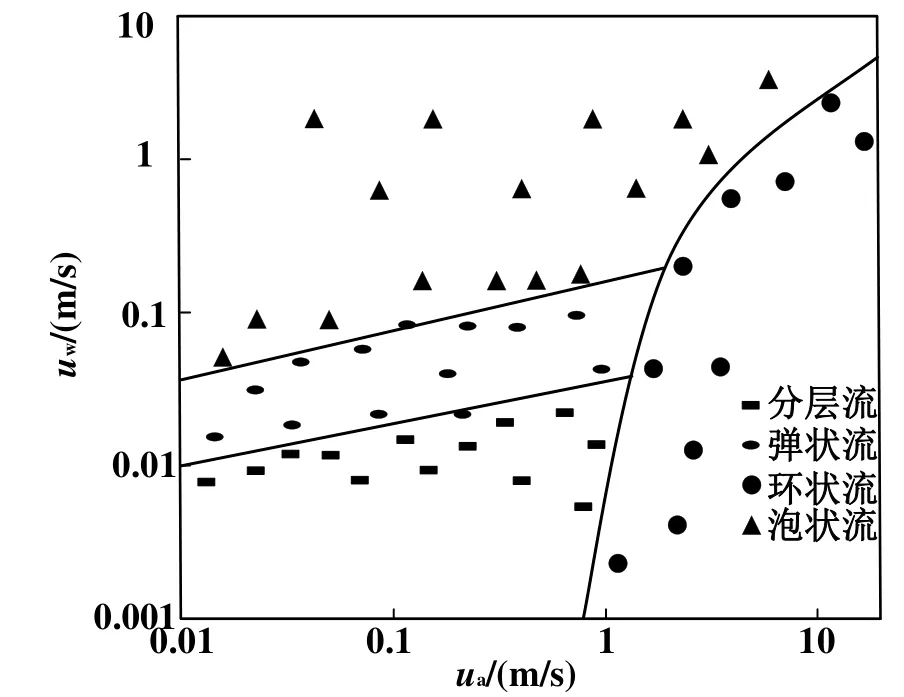
图3 水平管路中R32流型图模拟结果
4.3 水平管R32流型图与经验流型图的差异性
对模拟所得流型图的合理性进行评估,选取部分模拟点的流型结果与应用较为广泛的Baker经验流型图[9]查得的流型结果进行对比。从流型图中的分层流、弹状流、泡状流及环状流区域中各取7个模拟点,共28个模拟点。根据各模拟点对应的入口两相制冷剂质量流量和干度条件,可在Baker经验流型图查得其对应流型,对比结果如图4所示。
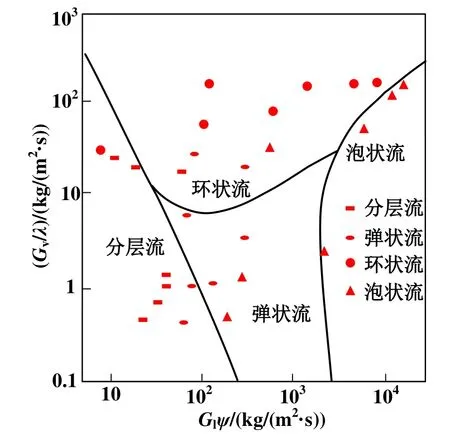
图4 R32流型图模拟结果与Baker经验流型图的结果对比
由图4可知,在所比较的28个工况点中,其中19个工况点在本文所得R32流型图及Baker经验流型图中查得的流型一致,剩余9个流型不一致的工况点在两流型图中的位置对应关系如图5所示。由图5可知,流型不一致工况点均在R32流型图中流型分界线附近。以图中的2号和3号工况点为例,2号和3号工况点在本文R32流型图中流型为弹状流,而在Baker经验流型图中查得的流型为层状流,且在本文R32流型图中2号和3号工况点正好在弹状流与分层流的分界线附近。流型分界线附近工况在两流型图中查得工况不一致的原因是因为流型分界线附近工况点最终流动稳定后的流型存在随机性,最终流型可能为分界线两侧流型的任意一种。综上所述,可以认为本文所开发的水平管内流型模拟方法及得到的流型图可较为准确的预测水平管内R32的流型转变规律。
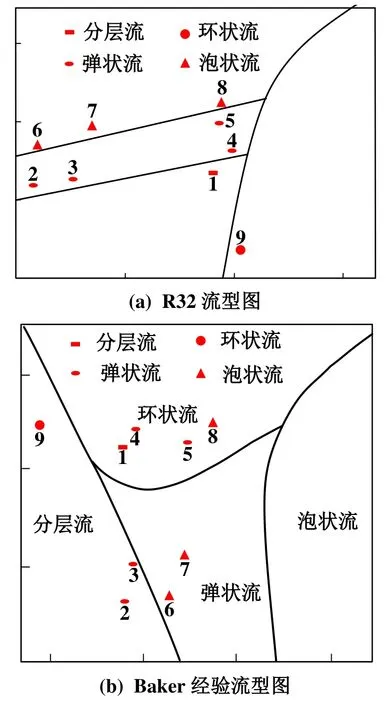
图5 不一致流型工况点在两流型图中的位置对应关系
5 结论
本文研究了R32在空调管路中流动过程的模拟方法,分析了R32在5 mm水平管中的流型变化规律,得出如下结论:
1)R32在水平管路中的两相流型基本形态受重力和惯性力的耦合影响,重力起主导作用时表现为分层流和弹状流,惯性力起主导作用时表现为环状流和泡状流;
2)液相表观速度是决定分层流向弹状流或泡状流转化的主要因素;分层流向弹状流转化的临界液相表观速度约为0.02 m/s,弹状流向泡状流转化的临界液相表观速度约为0.1 m/s;
3)气相表观速度是决定分层流、弹状流或泡状流向环状流转化的主要因素;分层流、弹状流或泡状流向环状流转化的临界气相表观速度为2 m/s;
4)基于流型模拟方法获得了水平管内R32流型图,与Baker经验流型图吻合良好,可用于预测制冷空调水平管路内R32的流型转变规律。

