典型汽轮发电机可倾瓦径向轴承冲击刚度研究

李 佳， 张 博， 丁 炜， 周相荣

(中国船舶重工集团公司第七〇四研究所，上海 200031)

轴承是汽轮发电机的重要部件，轴承动态特性对转子系统的动力性能有很大的影响，一直受到国内外专家及工程技术人员的重视，人们在轴承动态特性方面进行了大量的工作[1-4]。然而，对冲击状态下的轴承特性却鲜有研究。轴承冲击特性是汽轮发电机冲击响应模拟的前提，直接影响到碰摩、转子对中等仿真精度。汽轮发电机中常用的典型轴承为滑动轴承，由于滑动轴承工作机理复杂，轴承的几何形状、参数、工况各异，且油膜具有很强的非线性特征，因此滑动轴承的动态特性更多地仍依赖于试验研究。

滑动轴承的动态特性系数——刚度系数和阻尼系数的概念引入已有相当长的时间[5]，并在现代转子动力学的临界转速、不平衡响应以及稳定性等的计算、分析中获得了广泛应用并取得了丰硕成果。本文参照轴承动态特性描述并结合冲击试验，采用八个动力特征系数法来研究轴承冲击特性[6]。

1 径向可倾瓦滑动轴承基本动特性

1.1 轴承结构参数

以转速为4 500 r/min的汽轮发电机径向可倾瓦滑动轴承为研究对象，轴承参数如下：直径110 mm，长度58 mm，最小半径间隙0.20 mm，轴瓦张角90°，瓦数4块，支点角45°，40℃时的油运动粘度67.57 mm2/s，油密度870 kg/m3，进油温度40℃，进油压力0.1 MPa，轴承载荷4 025 N。

1.2 轴承动特性理论分析

根据文献[7]，采用8个简化动力特性系数分析可倾瓦轴承的刚度特性，图1显示了弹簧阻尼单元对轴承刚度的模拟。由文献[8]可知，4瓦块可倾瓦滑动轴承的8个简化动力特性系数当中，其交叉刚度和交叉阻尼在稳定状态下近似为0，故可简化为4参数来进行模拟。采用文献[9]中的数值计算方法求解雷诺方程和能量方程，获得径向可倾瓦滑动轴承动特性参数，如表1所示。

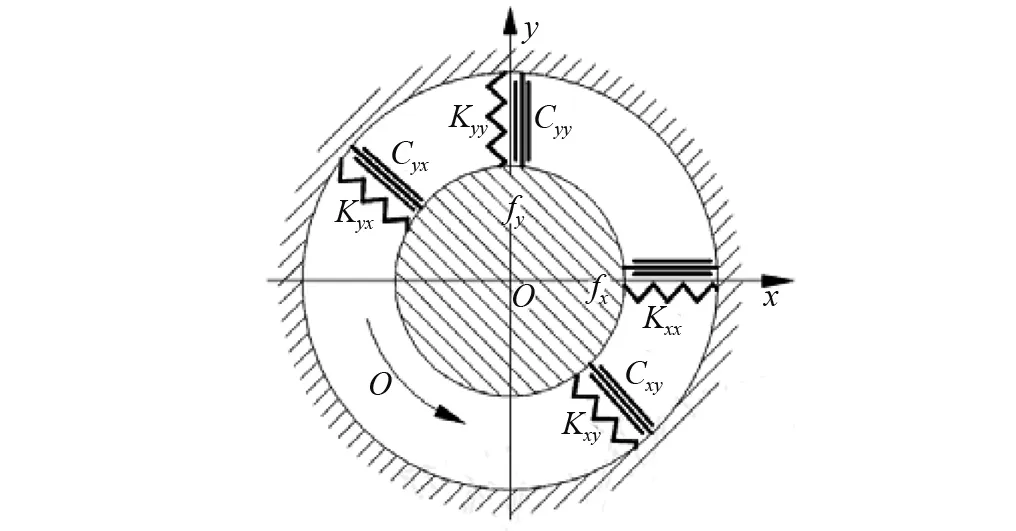
图1 轴承刚度力学模型Fig.1 Mechanical model to simulate the bearing’s stiffness

刚度参数/(N·m-1)KxxKxyKyxKyy2.2E+008002.2E+008阻尼参数/(N·s·m-1)CxxCxyCyxCyy4.9E+005004.9E+005

2 径向滑动轴承冲击试验

2.1 径向可倾瓦滑动轴承冲击试验台

径向可倾瓦滑动轴承冲击试验台由试验台本体、驱动系统、润滑系统以及测试系统组成，试验台通过橡胶隔振器弹性安装在冲击机上，主轴通过联轴器由驱动电机拖动，联轴器为膜片式联轴器，试验系统如图2所示。测试变量为冲击机台面加速度、径向滑动轴承端转子加速度、转子轴心位移、油膜压力、油温等。试验测点布置如图3所示，A为加速度传感器，D为电涡流传感器，T、P分别为内置于轴承内的温度传感器和压力传感器[10]。

图2 冲击试验现场照片Fig.2 Photo of the shock test device

2.2 冲击输入测试结果

冲击试验在中型冲击机上实施，砧板行程76 mm，落锤高度分45 cm，75 cm，100 cm，125 cm，140 cm五种工况。经隔振器隔离后的轴系基座表面垂向加速度为轴承系统的冲击输入载荷，通过加速度传感器直接测得，其包含了峰值、作用时间和波形3个特性，如图4～8所示。根据文献[11]，可采用冲击速度来对冲击激励进行描述和比较，冲击速度是冲击输入脉冲曲线下的面积，它包括了峰值、作用时间和波形3个因素，这样用一个物理量就可以完整地描述冲击输入特性了。对基座冲击加速度曲线进行积分，获得基座垂向冲击速度曲线，如图9～13所示。

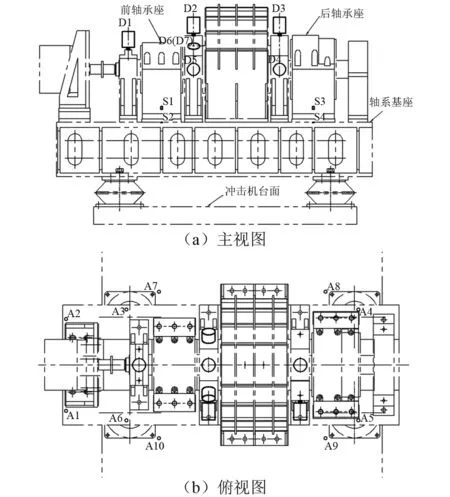
图3 测点布置示意图Fig.3 Layout of the measure points

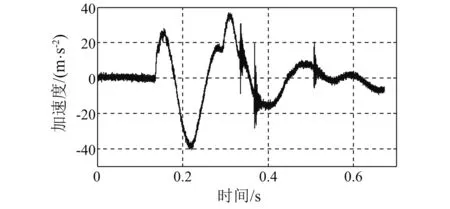
图4 基座冲击加速度(45 cm锤高)Fig.4 Shock acceleration of the supporting base (Height of hammer is 45 cm)

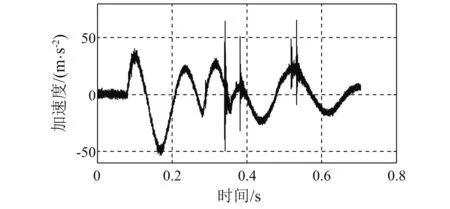
图5 基座冲击加速度(75 cm锤高)Fig.5 Shock acceleration of the supporting base (Height of hammer is 75 cm)

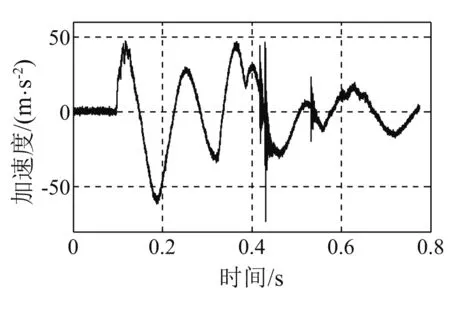
图6 基座冲击加速度(100 cm锤高)Fig.6 Shock acceleration of the supporting base (Height of hammer is 100 cm)

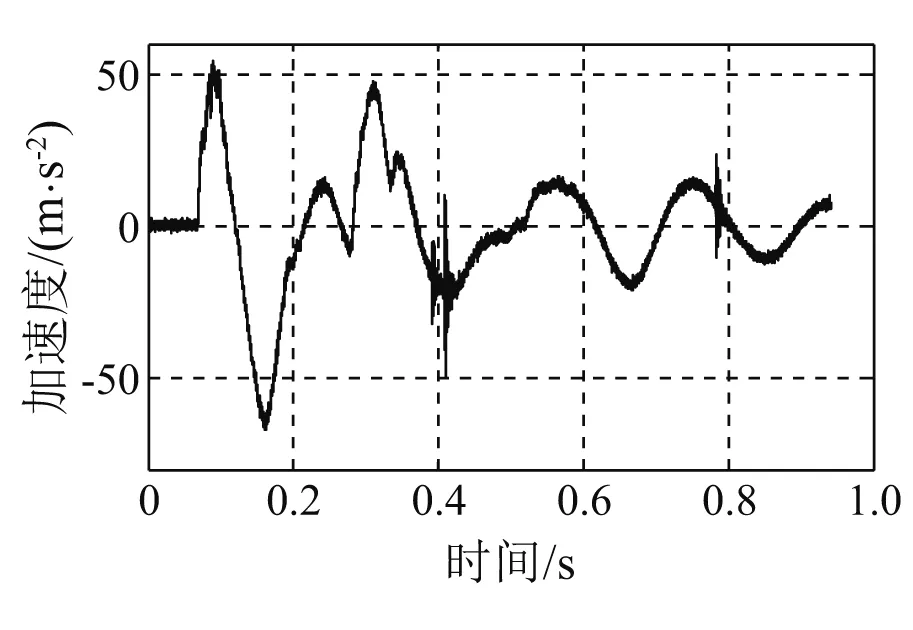
图7 基座冲击加速度(125 cm锤高)Fig.7 Shock acceleration of the supporting base (Height of hammer is 125 cm)

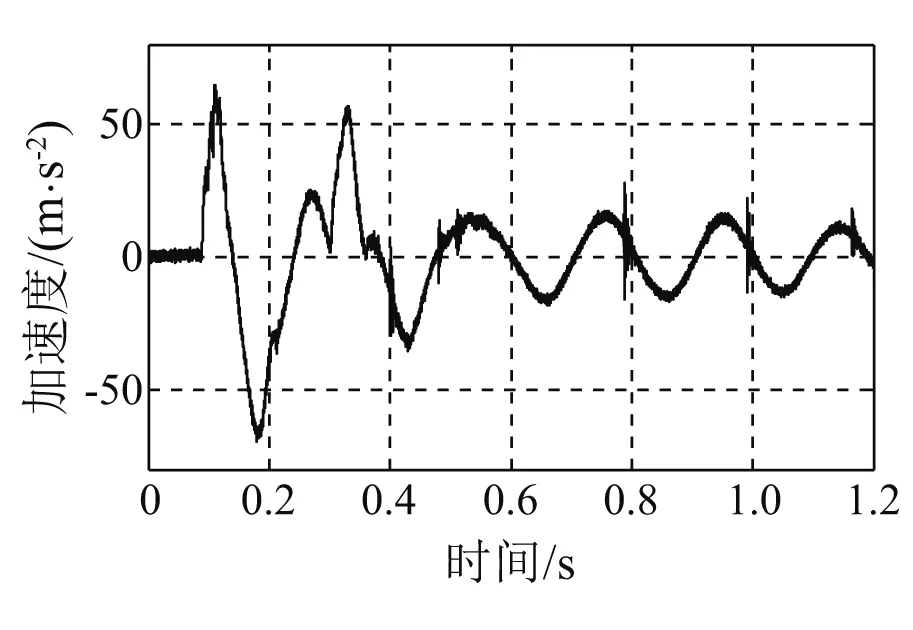
图8 基座冲击加速度(140 cm锤高)Fig.8 Shock acceleration of the supporting base (Height of hammer is 140 cm)

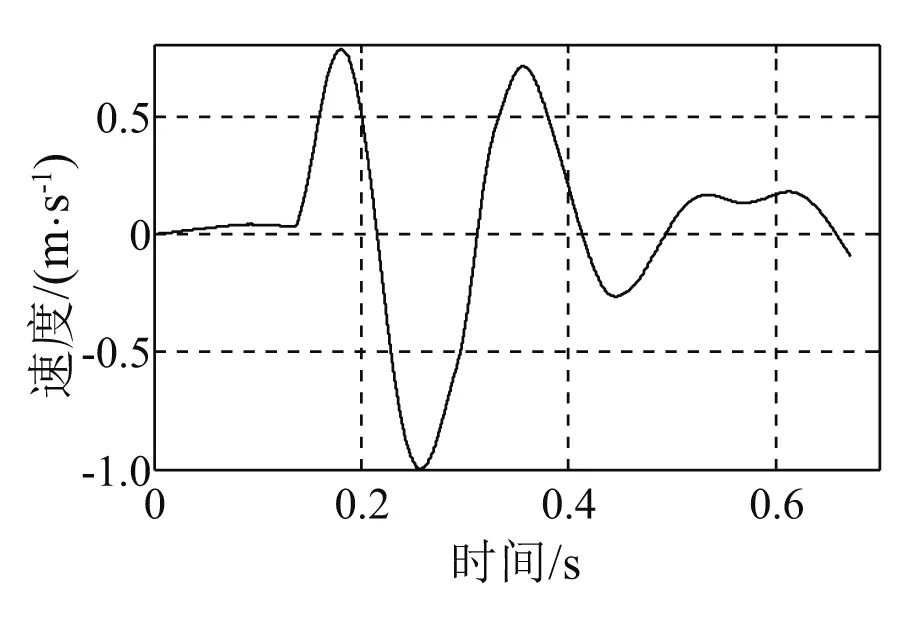
图9 基座冲击速度(45 cm锤高)Fig.9 Shock velocity of the supporting base (Height of hammer is 45 cm)

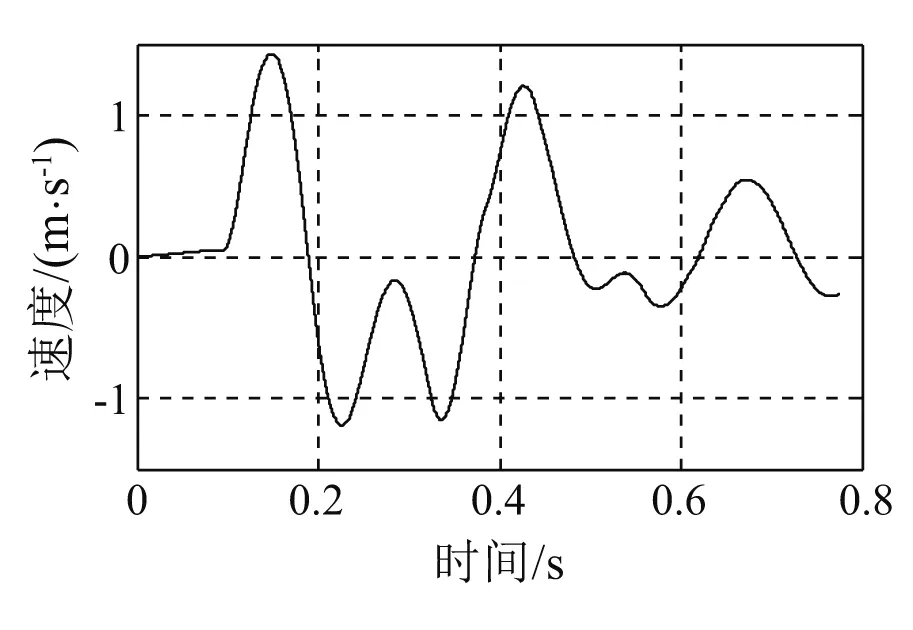
图11 基座冲击速度(100 cm锤高)Fig.11 Shock velocity of the supporting base (Height of hammer is 100 cm)

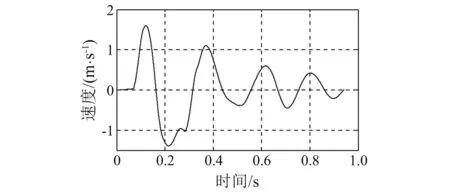
图12 基座冲击速度(125 cm锤高)Fig.12 Shock velocity of the supporting base (Height of hammer is 125 cm)

2.3 冲击响应测试结果

转子位移为轴系冲击响应，每一测点处的转子位移由电涡流传感器测得，电涡流传感器通过刚性较强的过渡支架安装于基座面板上，测得的转子位移理论上等于转子与基座的相对位移。测得的转子垂向位移曲线如图14～图18所示。

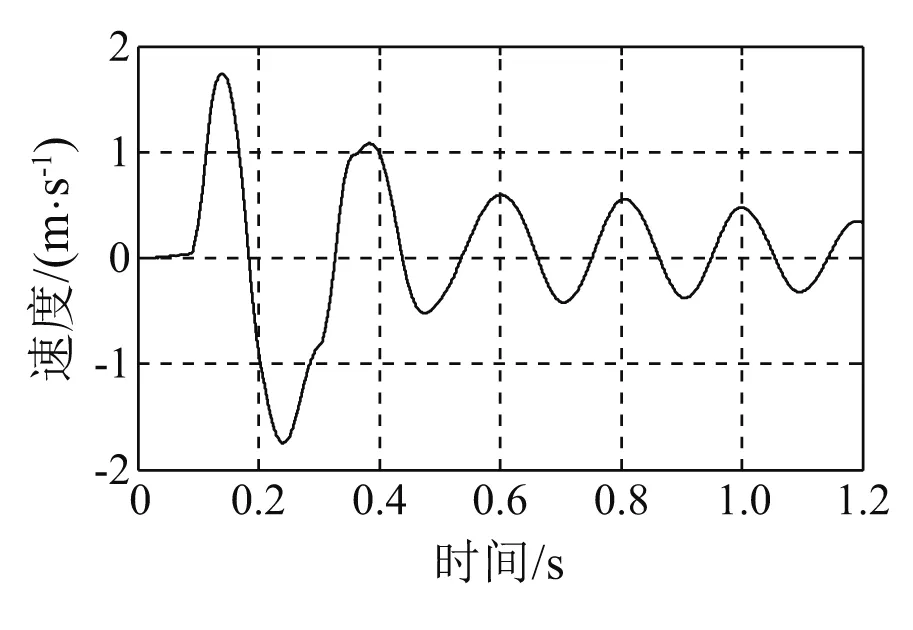
图13 基座冲击速度(140 m锤高)Fig.13 Shock velocity of the supporting base (Height of hammer is 140 cm)

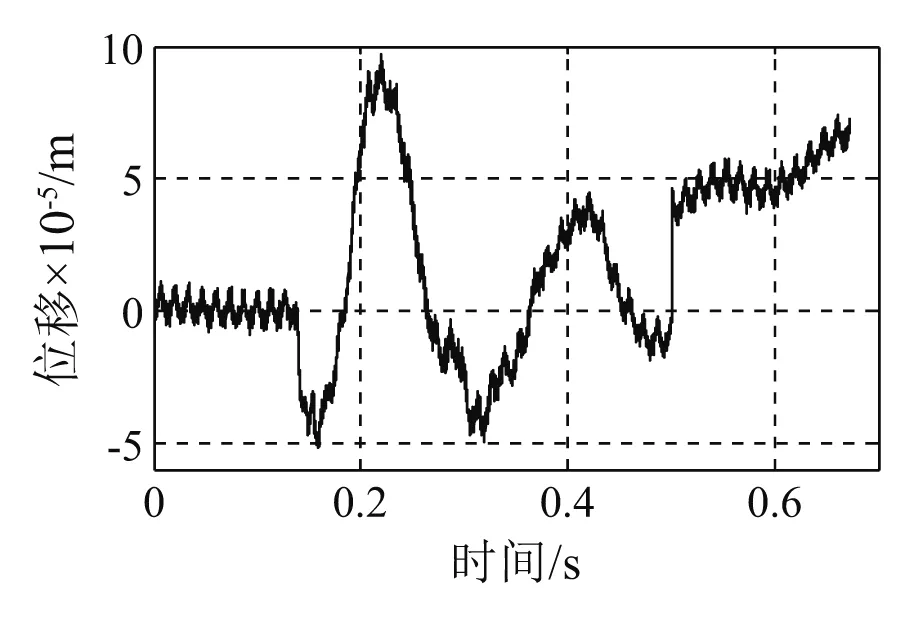
图14 转子垂向位移(45 cm锤高)Fig.14 Vertical displacement of the rotor(Height of hammer is 45 cm)

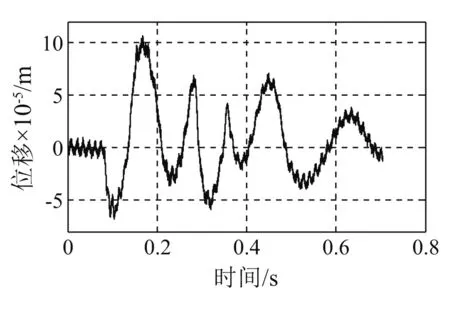
图15 转子垂向位移(75 cm锤高)Fig.15 Vertical displacement of the rotor (Height of hammer is 75 cm)

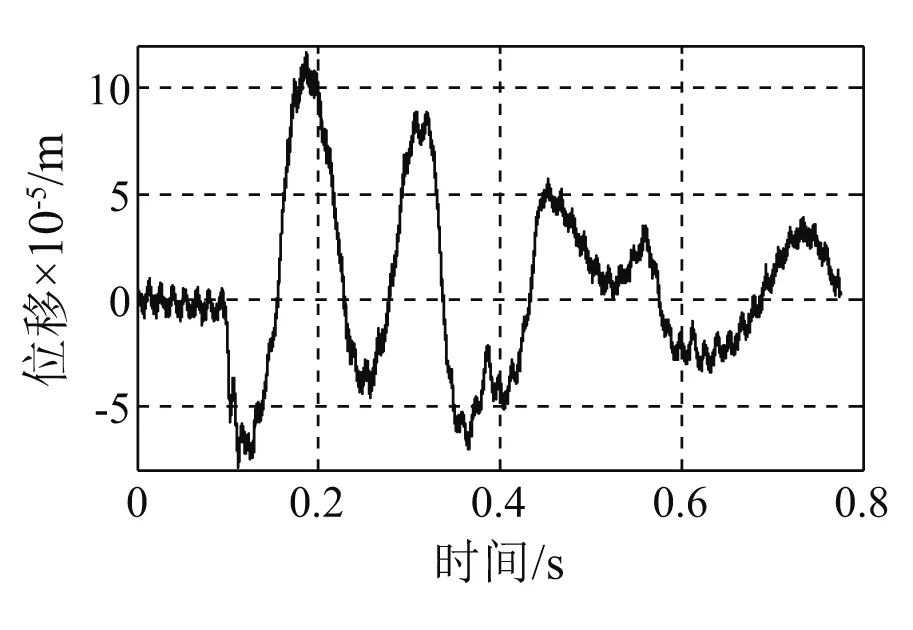
图16 转子垂向位移(100 cm锤高)Fig.16 Vertical displacement of the rotor (Height of hammer is 100 cm)

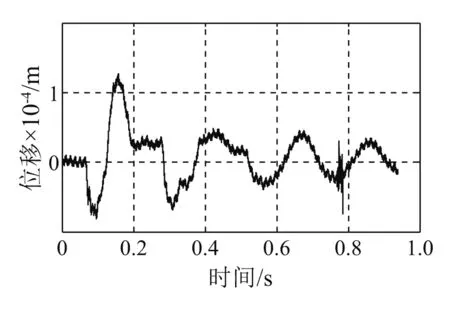
图17 转子垂向位移(125 cm锤高)Fig.17 Vertical displacement of the rotor (Height of hammer is 125 cm)

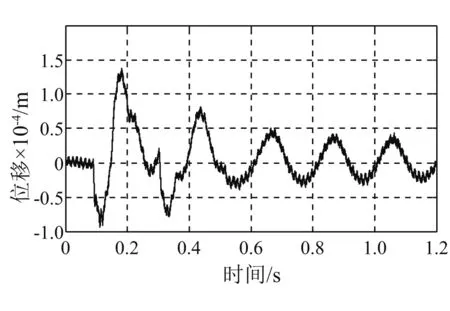
图18 转子垂向位移(140 cm锤高)Fig.18 Vertical displacement of the rotor (Height of hammer is 140 cm)

对比冲击响应与冲击输入，冲击响应(转子位移)与冲击输入(基座冲击加速度)的相位相反，脉宽基本一致。

3 基于冲击响应的轴承冲击刚度识别

3.1 基于冲击响应辨识轴承刚度的基本原理

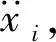
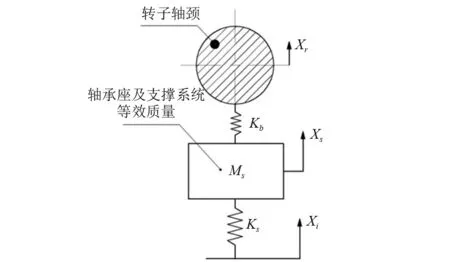
图19 轴承冲击刚度识别理论模型Fig.19 Simplified model to identify the bearing’s shock stiffness

3.2 试验装置冲击仿真模型

轴系试验装置有限元模型及轴系局部特征如图20～图21所示。

基座、轴承座、转子采用实体单元模拟，可倾瓦轴承的瓦块和油膜整体视为影响冲击响应的轴承黑箱，采用四参数(kxx，kyy，Cxx，Cyy)弹簧单元来模拟，且kyy=kxx=kb，Cyy=Cxx=Cb，kb为待识别冲击刚度参数，Cb按动刚度Cd进行取值。

3.3 轴承冲击刚度识别结果

从0.5kd～3.0kd范围内对kb进行取值，计算冲击响应，以位移曲线的第一个峰值为响应目标，当计算峰值与测试峰值相同时，认为轴承冲击刚度有效且(kb，Cd)的组合可用于冲击响应的模拟。识别结果如图22～图26所示，图中分别对测试曲线和计算曲线进行了100 Hz的低通滤波，使曲线趋于平滑。

从图22～图26可以看出，仿真计算得到的响应波形与时域波形比较一致，但存在一定的时间延迟，刚度识别的条件为计算结果的首峰值与测试结果相同。此外，次峰值和首脉宽的对比结果分别如表2和表3所示。

图21 轴系局部特征Fig.21 Specific model of the rotor-bearing system

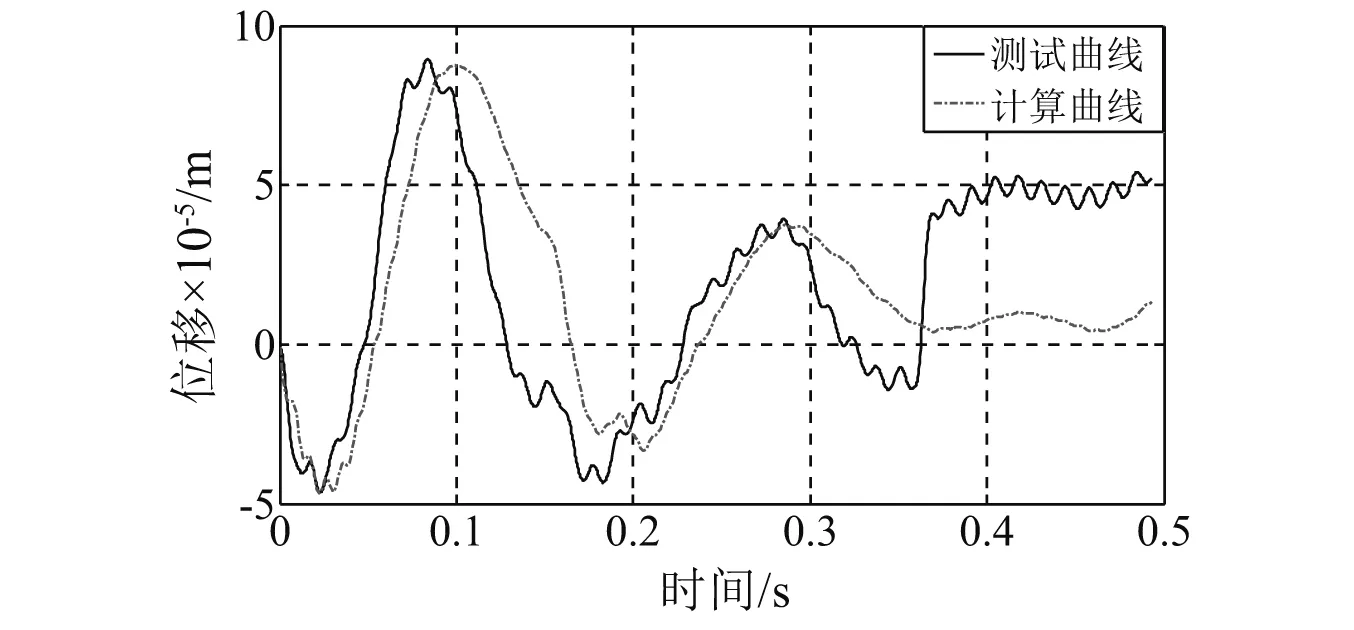
图22 45cm工况识别曲线(kb=3.95×108 N/m)Fig.22 Comparison curves for identifying the shock stiffness (Height of hammer is 45 cm；kb=3.95×108 N/m)

图23 75 cm工况识别曲线(kb=4.41×108 N/m)Fig.23 Comparison curves for identifying the shock stiffness (Height of hammer is 75 cm；kb=4.41×108 N/m)

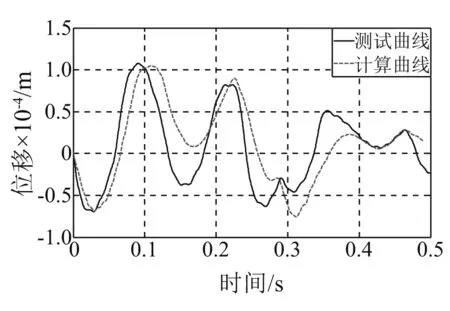
图24 100 cm工况识别曲线 (kb=4.78×108 N/m)Fig.24 Comparison curves for identifying the shock stiffness(Height of hammer is 100 cm；kb=4.78×108 N/m)

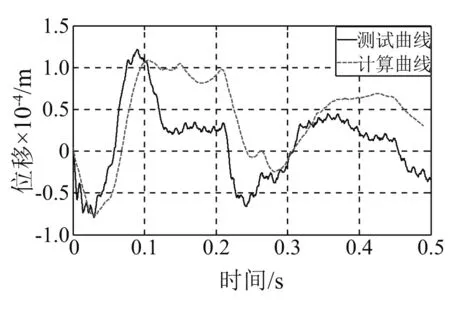
图25 125 cm工况识别曲线 (kb=5.14×108 N/m)Fig.25 Comparison curves for identifying the shock stiffness(Height of hammer is 125 cm；kb=5.14×108 N/m)

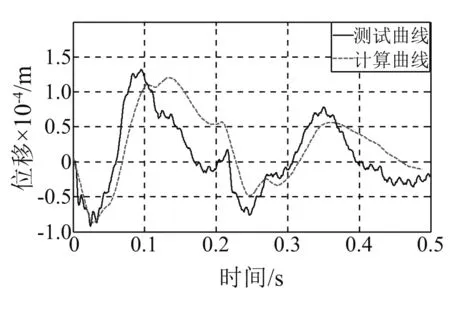
图26 140 cm工况识别曲线 (kb=5.36×108 N/m)Fig.26 Comparison curves for identifying the shock stiffness(Height of hammer is 140 cm；kb=5.36×108 N/m)

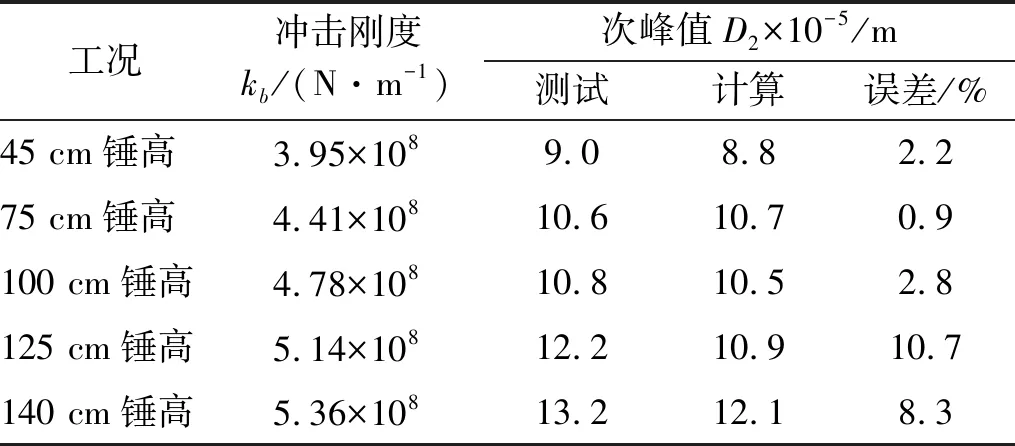
表2 计算与测试结果对比表(次峰值对比)Tab.2 Comparison between the simulation and test for the 2nd peak

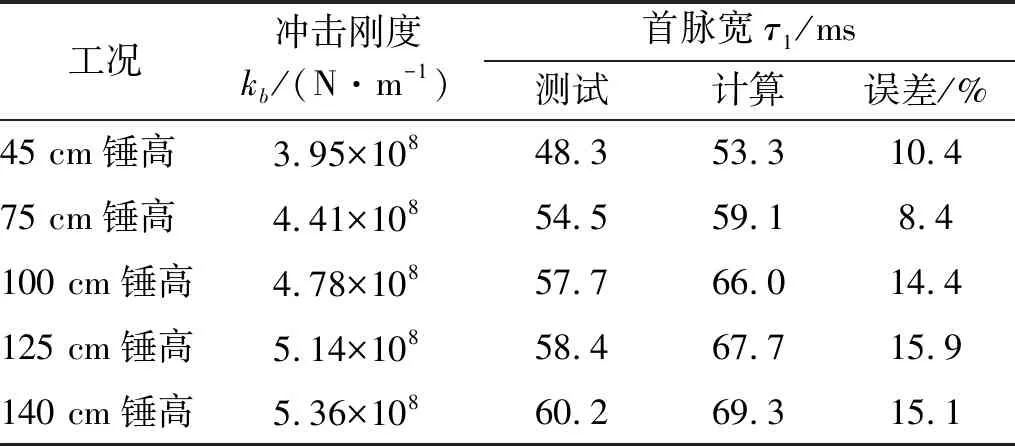
表3 计算与测试结果对比表(首脉宽对比)Tab.3 Comparison between the simulation and test for the 1st pulse width

根据表2～表3中的轴承冲击刚度识别结果，比较冲击刚度、动刚度与冲击速度的关系，如表4所示。

当冲击速度为0 m/s时，轴承冲击刚度等于动刚度。通过分析表4中的冲击刚度识别结果，发现轴承冲动比与冲击速度近似呈线性关系，为进一步分析冲动比与冲击速度之间的规律，对冲动比与冲击速度之间的关系进行拟合，冲动比(δ)与冲击速度(V)之间的关系式为

δ=C+D×V

(1)

式中：C和D为常数。其中，C=1，代表冲击速度为0时轴承冲击刚度等于动刚度，通过最小二乘法求得D值为0.83，冲动比与冲击速度的拟合关系对比曲线，如图 27所示。

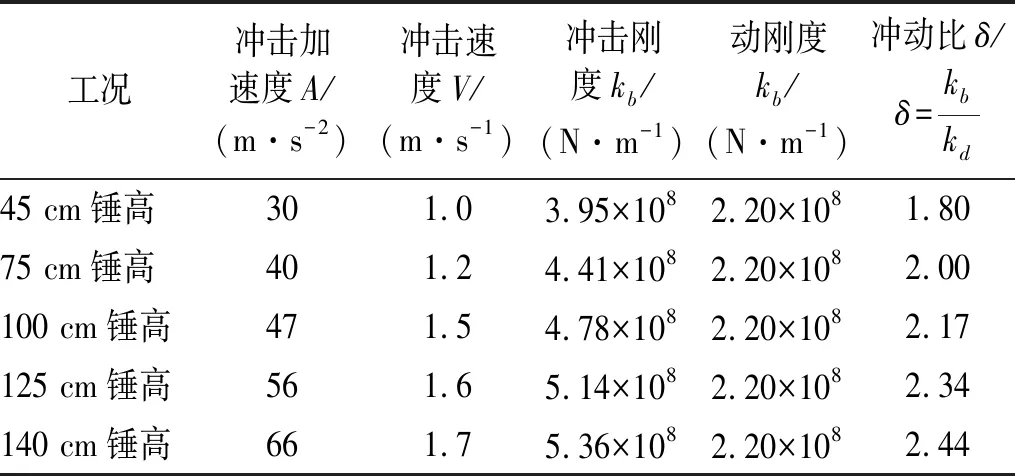
表4 轴承冲击刚度识别结果Tab.4 Identification results for the bearing’s shock stiffness

图27 轴承刚度冲动比与冲击速度关系曲线Fig.27 Curves for the relation of δ to V

从图 27可以看出，轴承刚度冲动比与冲击速度近似呈线性关系，关系式δ=1+0.83×V可以较准确地反映冲动比与冲击速度的关系。

4 结 论

本文通过搭建径向可倾瓦滑动轴承冲击试验台并实施不同冲击能量下的冲击试验，采用试验结合数值仿真的研究手段，结合黑箱法识别了径向可倾瓦滑动轴承的冲击刚度，并通过分析获得了工程实用的冲动比与冲击速度之间的拟合关系。得到以下结论：

(1) 径向可倾瓦滑动轴承的冲击特性可采用等值非交叉刚度Kxx和Kyy来模拟，该模拟方法在冲击响应的前两个峰值具有较好的适用性。

(2) 轴承冲击刚度与动刚度之比冲动比(δ)与冲击速度(V)存在δ=1+0.83×V的拟合关系。拟合曲线与原识别曲线具有较好的符合性，本方法为滑动轴承冲击刚度的识别以及为转子-轴承系统的冲击动力学研究提供了理论依据。