基于小波多尺度变换的储气库井管柱非线性振动特性研究
闫 行, 闫怡飞, 闫相祯
(1.中国石油大学 储运与建筑工程学院, 山东 青岛 266580;2. 中国石油大学 机电工程学院, 山东 青岛 266580)
储气库井管柱作为地下储气库运行的主要工具,面临地质构造复杂和大流量强注强采的苛刻要求,其服役周期的安全性是储气库井安全运行的关键问题[1-4]。在储气库井作业过程中,井下压力波动、井深结构等产生的持续交变应力诱发注采管柱振动。同时,完井管柱受井身结构限制和油套间环空带压影响,管柱发生振动位移时易产生碰撞和变形,甚至造成气体泄漏、封隔器失效和管柱疲劳破坏等井下事故。因此合理分析储气库井管柱非线性振动特性对储气库井工程安全研究具有十分重要的意义[5-8]。国内外研究学者对管柱振动已经进行了大量研究,Lubinski等[9]研究了在轴压及内外压作用下油管发生的螺旋弯曲,并发现内压变化引起管柱失稳现象。阳明君等[10]对高产气井带封隔器油管柱振动进行数值模拟,分析结果表明高速气流诱发管柱振动并造成底部管柱屈曲损失。窦益华等[11]一方面建立改进的输流管道的水锤分析模型,并模拟研究了开关井工况下完井管柱振动的应力分布,发现开关井工况下完井管柱易发生剧烈振动。以上研究为本文工作的开展奠定了良好的基础,但未充分考虑作业过程储气库井井筒结构对管柱的影响,导致注采管柱非线性振动的研究还不够充分。
随着小波分析理论和算法的发展,在工程应用分析方面取得了良好的发展成果。其优点是既保留了传统傅里叶分析的优点,又弥补了其无法进行局部分析的不足,适用于湍流及众多非线性科学等领域。国内外已有的工程应用成果体现了目前小波分析方法的发展方向,为本文研究工作的开展奠定了良好的基础和参考价值[12-13]。
为探究储气库井注气过程管柱非线性振动特性,首先,根据储气库井筒结构特点建立储气库井管柱非线性振动分析方法,通过数值求解得到管柱非线性的数学方程;其次,根据振动模型建立ANSYS仿真模型,模拟分析管柱的固有特性并与数学模型结果进行对比,同时对储气库井管柱进行瞬态动力学响应分析,得到管柱振动效果变化规律;最后,结合现场工况搭建储气库井管柱振动实验研究装置,设计振动信号数据采集终端,通过注气过程管柱非线性振动实验得到振动特征数据。以实际储气库井J03-H1为例,分析注气过程管柱压力、管壁速度和幅值等振动效果变化规律。为深入开展储气库井注采管柱振动分析提供了一种新的思路和方法。
1 储气库井管柱非线性振动分析方法
1.1 柔性约束下管柱力学模型
基于弹性力学和管柱力学相关理论,建立储气库井管柱力学分析模型[14-15],如图1所示。考虑注采管柱生产实际工作条件,井身结构和井下工具分布较为复杂,包括表层套管、技术套管、生产套管、环空填充液、注采管柱、永久封隔器、尾管等。为了便于进行数值分析,假定井下管柱为长直杆件,并且是各向同性、均匀连续的线弹性体;将井下管柱看成一个整体,平均分为n等分。图1还给出了衰竭油气藏储气库井注采过程i段管柱力学分析模型。图中hi、r和R分别表示研究注采管柱i分段的长度和内外径。

图1 储气库井管柱力学分析模型Fig.1 Non-linear vibration mechanics model of well string of gas storage reservoir
油套管间填充环空保护液,其作用是减轻套管头或封隔器承受的油藏压力,降低油管柱与环空之间的压差等,由于多组分填充液具有优异的剪切稳定性和温粘特性,可产生具有液体弹簧效果的柔性约束,因此分析模型中添加变刚度弹簧结构。
根据图1所示油套横截断面,在初始状态下管内压为p0,液体体积为v,当管柱受持续激励发生径向位移时,环空压力为p1,液体体积变化为Δv。假定环空内温度为常数,则环空填充液的弹簧效应力为:
(1)
式中:Δp=p1-p0,增大或减少液体体积v,从而改变弹簧的刚度k。
当Δv→0时,
(2)
式中:液体弹簧刚度k,与体积弹性模量、环空横截面积成正比。
1.2 管柱非线性振动计算模型
基于Rayleigh-Love杆理论和管柱力学[15],储气库井第i段注采管柱的非线性振动方程(3)可表示为:

(3)
式中:Ei,Ai,ρi,vi,δi分别表示第i部分井下管柱的弹性模量、横截面积、密度、Poisson比、阻尼系数;ui=ui(z,t)表示第i部分井下管柱的纵向位移;fi表示第i部分井下管柱上、下端面单位长度作用力之和。用ci表示井下管柱接触面上单位长度方向上的纵向剪切复刚度,Δf为环空压力值。则fi及Ai可以表示为:
fi=ciui(z,t)
(4)
(5)
相邻井下管柱微元段分界面两侧的位移需满足的连续性条件为
(6)

(7)
1.3 小波变换求解管柱非线性
储气库循环注采过程是多时间尺度的持续过程,小波函数变换可分析并给出管柱频域信息。同时,与傅里叶函数变换相比,小波函数在求解非线性动力学方程时,时域和频域上都具有很好的局域性,能够提高求解计算精度和效率。因此,本文引入小波函数求解注采管柱的非线性振动方程,其中小波函数公式为[13]:
(8)
式中:w0为小波的中心频率。
考虑井下管柱受持续激励初始阶段,第i部分井下管柱的初始位移和速度均等于 0,通过小波函数对方程(3)进行变换得到(9):
(9)
式中:Ui=Ui(z,s)为ui(z,t)的小波变换。
为便于求解,设定
(10)
β=6ρi+Cit2
(11)
(12)
则上式方程可简化为
(13)
解得:
Ui(z,s)=C1er1+C2er2
(14)
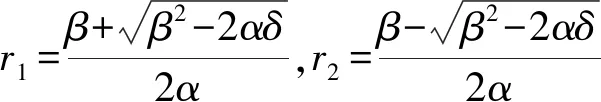
储气库地层可看作是无限大地层(D≥0,t≥0),初始储层压力为 ,则从井筒注气的过程可以看作流体成平面径向流流入地层,因此注气后地层压力随时间t和半径D的关系[16]为:
(15)
式中:Ggi为注气重量流量,χ为导压系数。
令Fi(z,t)=φ(z,t)Ai,则井下底部管柱振动应满足以下条件:
Fi(z,t)|z=0+qi(z,t)=0
(16)
Ui(z,s)|h=0
(17)
将两个关系代入解的C1、C2的关系式:
(18)
C1er1+C2er2=0
(19)

代入求得:
(20)
(21)
井下完井管柱ti时刻振动位移为:
(22)
相应的振动频域公式为:
(23)
为求解井筒管柱的固有频率,将式(3)进行无量纲化得到式(24):
(24)

通过分离系数法求解式(27)可得到井筒内管柱的多阶频率值,其中第一、二阶的储气库井管柱频率值分别为:
(25)
(26)
其中:
2 工程实例分析
2.1 现场数据
某衰竭油气藏储气库J03区块井群位于华南地域,由原主力生产井改建而成,均具有天然良好的密封构造。建成后用以满足目前陕京线、陕京二线、西气东输等长输管线对储气库季节及安全调峰气量的迫切需求[17],因此储气库群设计和安全运行要求比较高。本文主要针对储气库井J03-H1进行分析,现场地质工况包括:
储层条件:储层以成层分布的溶蚀孔洞为主,岩性致密;
储库数据:原始地层压力30.4 MPa,储层厚度12 m,压力系数0.18;
场地条件:地震峰值加速度0.15g,地震基本烈度Ⅶ度。

表1 储气库设计参数Tab.1 Parameters of underground gas storage
2.2 三维有限元模型建立
借助ANSYS软件以现场工况参数建立衰竭油气藏储气库井管柱注气过程非线性振动有限元分析模型。所建模型采用管单元Pipe288单元模拟,选取单元具有拉压、弯曲和扭转性能。单元的每个节点有6个自由度。数值积分采Newton-CoteS积分。为模拟油套间环空填充液的黏弹性作用,在注采管柱有限元模型的每个单元两端添加非线性弹簧单元Combin39,添加方向包括管轴方向、水平方向和垂直方向。储气库井管柱三维有限元模型图如图2所示,假定Combin39单元只允许有轴向变形,管柱选用φ114.3×14.22钢制管材,其基本参数见表2。

表2 储气库注气管柱参数Tab.2 Parameters of reservoir
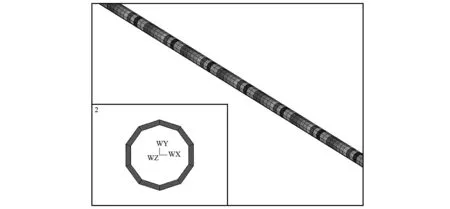
(a) 注采管柱有限元模型
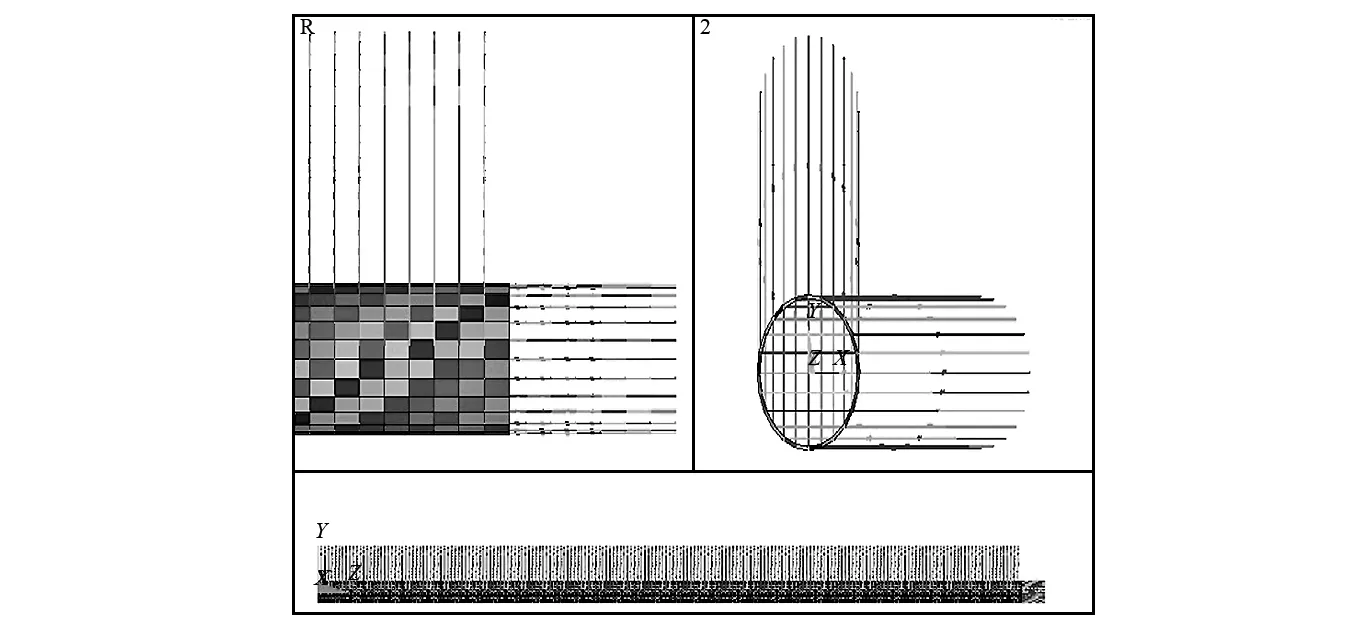
(b) 注采管柱弹簧单元效果图 图2 储气库井管柱三维有限元模型图Fig.2 Three-dimensional finite element model of the gas storage well string
2.3 管柱固有特性分析
为验证储气库井管柱非线性振动分析方法的准确性和精度[19-20],笔者采用Matlab软件编制了本文的计算模型,对储气库井J03-H1的某一生产工况进行了模拟计算,同时利用三维有限元模型对同一生产工况的注采管柱进行多周期的谐响应分析。模拟条件设定注气压力35 MPa,管柱轴向力为20 kN,相位角为0,载荷频率范围为0~0.5 Hz。并将本文模型计算所得管柱频率结果与有限元模型计算结果进行了对比,如图3所示。
图3给出了本文有无考虑环空约束计算结果与谐响应分析结果的对比。由计算结果对比可知,当油管柱长度一定时,考虑环空带压约束(CAP)所得固有频率值较未考虑环空带压约束(NAP)的计算值更大,与有限元分析结果比较接近。当管长约400 m时,NAP的固有频率值约为 0.378×10-1Hz,CAP的计算值约为0.391×10-1Hz,两者差值在3.35%,且数值计算值为0.402×10-1Hz,表明本文模型计算结果的具备一定稳定性。

图3 同一工况管柱固有频率对比曲线Fig.3 The curve of relationship between length and nature frequency for two conditions
由图3可知,随着管长的增加,环空带压约束对管柱的固有频率影响逐渐增加,两种边界条件下固有频率的差值不断增大。当管长小于300 m时,环空约束对管柱固有频率影响作用不大,当管长约200 m时,NAP的固有频率值为 0.865×10-1Hz,CAP的管柱固有频率值为0.874×10-1Hz,差值约在1.06%;当管长超过400 m后,CAP的管柱频率值明显大于NAP的频率值,当管长约600 m时,NAP的管柱频率值为 0.129×10-1Hz,CAP的管柱固有频率值为0.161×10-1Hz,差值约在24.01%;当管长约800 m时,NAP的固有频率值为 0.118×10-1Hz,CAP的管柱固有频率值为0.149×10-1Hz,差值约在26.48%。结果说明当管柱足够长时,进行相关管柱安全设计时必须要考虑油套环空对注采管柱的约束作用。
图4给出储气库井管柱系统阻尼对管柱振动影响分析图。由结果曲线可以看出,当激扰频率接近管柱某一阶频率时,管柱幅值会急剧变大,产生了“马鞍状”峰值结构,明显大于其它频率所产生的幅值,可认定该工况下管柱发生共振,相应激扰频率为诱发管柱共振的激扰频域。当阻尼δ= 0.10时,管柱发生“马鞍状”特性的激扰频率分别为0.030 1 Hz、0.054 6 Hz、0.090 2 Hz,对应的模拟幅值为0.357 m、0.185 m和0.122 m,与软件输出结果差值分别为9.23%、4.86%和4.91%,表明幅值特性计算结果可信。
同时由图4(a)~(c)可知,随着阻尼的增加,对于同一激扰频率下,阻尼不同管柱的幅值也会相应发生改变。当管柱系统阻尼δ分别为0.10、0.15、0.20时,管柱“马鞍状”特性幅值(f=0.030 1 Hz)分别0.357 m、0.315 m和0.225 m,说明阻尼越大,管柱发生共振时所产生的幅值会越小。

图4 不同阻尼对管柱影响到幅频特性图Fig.4 The curve of the amplitude frequency and phase
根据油管完整性指数公式[21-22]为
IIT=γ‖max{ψ1,ψ2}·[δ(η1),δ(η2)]‖
(27)
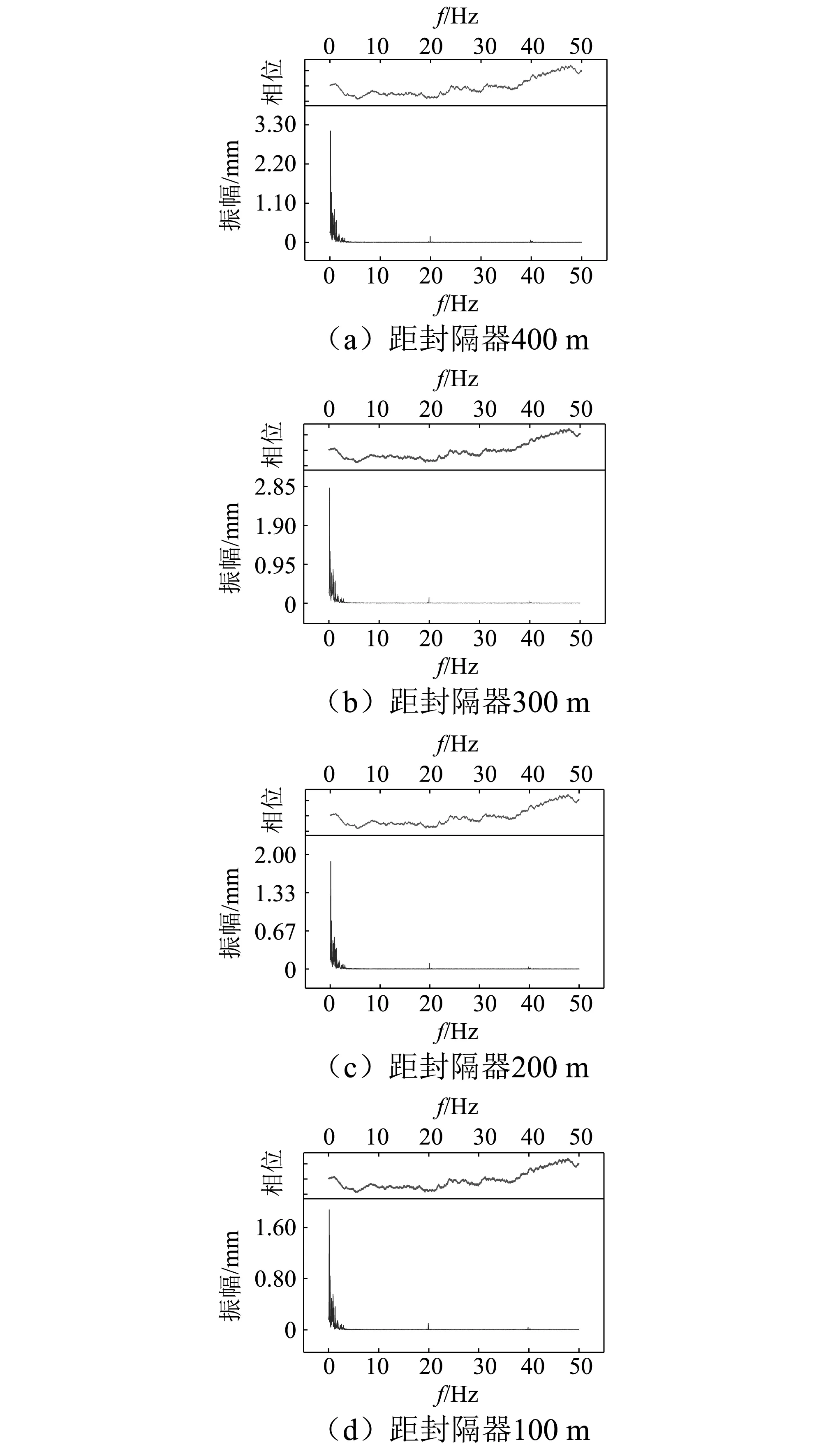
油管完整性指数IIT的取值范围为[0, 1]。当IIT=1时,油管失效;当0 通过对注采管柱的固有频率特性及谐响应分析,研究注采压力波动对注采管柱引起的激扰作用,得到激扰频率对管柱振动的诱发效果。同时考虑储气库多周期的强采强注生产,压力波动的瞬时性和多变性会对诱发管柱振动产生较大影响,因此需进一步对气藏型储气库井管柱进行瞬态动力学响应分析[18]。 由于高速气流的不稳定性因素,稳产过程中储气库井保持的注采压力存在一定范围内的压力波动,即真实载荷存在一定波动范围。为更接近真实工况,在进行注采管柱瞬态动力响应分析时,添加间歇随机波动压力。图5所示对三维管柱模型施加的内压值。静压P0为30 MPa,波动压差为10 MPa,运行时间为30 s。 图5 模型施加的内压值Fig.5 Internal pressure values imposed by the model 图6 (a)~(c)所示为距离封隔器不同位置处管柱瞬态动力响应分析结果。由图6可以得知,当注采管柱稳态注采过程中,由于高速的天然气的不稳定性会造成内压波动,其波动会造成管柱轴向位移产生周期性的扰动,越接近封隔器位置,管柱的振幅、速度和加速度会越小;越远离封隔器位置,其振幅、速度和加速度会越大。考虑距离封隔器距离越远,管柱的柔度会增加,其弹性变形以及运动的空间也会增加。由此可以得知,稳定的注采过程近封隔器端管柱振动效果较小,且主要振动为管柱纵向振动。 图6 管柱瞬态动力响应分析结果Fig.6 Pipeline transient dynamic response analysis results 为研究压力波动对管柱振动频域的影响,分别对距离封隔器100 m、200 m、300 m和400 m的数值结果进行变换分析,如图7所示。结果表明:距封隔器不同位置处测点的管柱振动频域分布趋势具有相似性,当处于低频压力激励区,管柱的频域响应幅值较大,说明压力激励频率接近系统低阶固有频率时,管柱将发生明显振动,即该工况下管柱发生共振,由此可见低频压力波动是生产过程管柱产生振动的重要激励源。 图7 模拟数据变化分析结果Fig.7 Simulation data change analysis results 同时从图 7 可知,距离封隔器400 m、300 m、200 m和100 m处的管柱振动幅值呈下降趋势,其中距离封隔器400 m处的管柱最大幅值约为3.18 mm,距离封隔器100 m处的分析最大幅值约为1.71 mm,近封隔器端的管柱振动幅值并未随管柱自身频率的降低而增长,主要原因是井底封隔器对管柱具有良好的约束作用。因此为减缓交变载荷所带来的疲劳效应,可选用适宜规格的封隔器装置以保障管柱安全生产。 根据现场工况数据,搭建实验装置。实验所用油管柱全长约8.5 m,设计压力10 MPa,允许的最高压力16 MPa ,由不锈钢管构成。实验装置如图8所示,按照“直井段——井斜段——水平段——储气库”的模式设置,同时在起终点间设置8个测点,设置位置分别在直井段、井斜段、水平段等处,可根据实验需要改变测点位置。实验所用注气为带压空气,带压空气与天然气的物理性质相近,能够满足实验效果和装置安全的需要。该实验装置系统在设计时与实际的储气库井工况进行了相似性分析(见表3),取得较好相似性结果,可以实现储气库井管柱注气过程非线性振动的监测和模拟功能 。 图8 实验装置图Fig.8 The Experimental setup Tab.3 Comparison of experimental tubings and real tubings 类型现场油管/mm外径内径壁厚实验油管/mm外径内径壁厚比例参数114.3100.536.8853.813.3510.2330∶1 所建实验系统包括硬件单元和数据采集单元。其中硬件单元由空压机、增压泵、储气罐、油管管路、传感器等组成,实验硬件单元布置如图9所示。实验过程中可由空压机提供流量,由增压泵和储气罐提供带压气体,由气体流量质量控制器控制气体流入压力,由差压计测量每个实验管段的压差。 图9 地下储气库注采模拟硬件实验装置Fig.9 Simulation hardware experiment device for underground gas storage 为实时采集测点数据, 所用数据采集单元可测量每个管段测点的近壁压力、位移和速度值,即在测点位置添加压力传感器(PM)、位移传感器(DM)、速度传感器(VM)等数据元件。储气库非线性振动实验测点数据元件分布如图10所示 。 图10 储气库非线性振动测点数据元件分布图Fig.10 Gas storage vibration data element distribution 该装置建立的储气库非线性振动的实时数据采集系统 ,还包括型号为PCI-1711的常规数据采集卡以及型号为PCI-4472的动态数据数据采集卡,均具有独特的电路设计和完善的数据采集与控制功能。针对实验信号的幅值和频率变化速度极快等情况,所用采集卡可以进行高速数据的采集,最终保证了数据采集的实时性和实验精度 。 实验流程如下:实验采用气源为压缩空气,气体经压缩机加压,通过冷干机和过滤器除去水分,经过高压缩机泵入铺设管段 ,利用流量控制球阀实现气体稳压流出后, 同时打开模拟井底和井口的气体阀门,带压气体经“直井段——井斜段——水平段”进入模拟储库的高压储罐,保持带压气体流出并记录传感器反馈数据,最后关闭气瓶,待油管柱内带压气体释放完毕完成该阶段实验,并以此操作步骤最终完成衰竭油气藏储气库井管柱注气过程非线性振动模拟实验。 参考Tijsseling提出的简化条件[19-20],忽略油管重力对实验结果的影响,且认为整个管路的转动惯量为零。实验模拟工况:注气流量 30×104m3·d-1,沿程压降为8 MPa,狗腿度为9°/30 m,油压33 MPa,井口温度T=25℃,得到油管柱近壁压力沿程分布实验结果并与现场结果对比,如表4所示。 表4给出了油管柱A、B、C和D等处测点(直井段、井斜段和水平段)的近壁压力沿程分布实验结果与现场结果对比。结果表明,实验测得各段压力分布与现场结果的相对误差分别为6.27%、7.58%、4.82%和5.31%,满足实际工程需要,并且本文实验测定结果的方差最大为3.85,而现场结果方差最大为3.99,说明用本文实验测2得的计算结果比现场结果波动要小,可见上述实验设计具备一定稳定性和实用性。为研究储气库井注气过程管柱振动特性,进一步分析注气过程管壁压力、管壁速度和幅值等振动效果变化规律。 表4 油管柱近壁压力实验结果与现场结果对比Tab.4 Near-wall pressure test results and field results (1)管柱近壁压力变化分析 图11为选取的测定A、B和C等测点的注气过程管壁近壁压力随时间的变化情况。从图11(a)~(c)可以看出,管壁近壁压力迅速上升,压力稳定在某一区间范围波动内,且具有周期性。其中图11(a)所示近注气口的直井段内气体压力的震荡呈周期性变化,且变化幅度较大,从t=0.136 s后保持稳定。图11(b)所示井斜段内近壁压力在t=0.164 s后呈多段震荡,变化幅度增大。说明储气开启段和井斜段近壁压力变化较大,对管柱作用比较明显。图11(c)所示水平段近壁压力在传输过程中保持稳定,变化幅度逐渐减小,交替周期逐渐变长。 图11 注气过程管壁近壁压力随时间的变化情况Fig.11 Variation of pressure in the wall of the pipe wall with time during gas injection (2)管壁速度变化 图12为A、B和C等测点的注气过程管壁速度随时间的变化情况。从图12 (a)~(c) 时程曲线可以看出,数值模拟的油管柱振动速度与实验值基本一致。在持续注入过程中,近注气口段、井斜段、水平段的油管柱管壁速度均呈周期性变速运动,并随着注入流量的增加,各段油管柱运动速度变化明显,趋势为先快后慢。同时图12(a)表明,当流量控制阀开启后, 注入气 图12 注气过程管壁速度随时间的变化情况Fig.12 Variation of tube wall Velocity with time in gas injection 迅速进入实验装置内,近注气口段管壁速度迅速上升,并逐渐稳定在某一区间范围内,且具有周期性,波动频率较大。图12(b)表明注气进入井斜段后,由于沿程流动阻力和壁面摩擦等影响,管壁速度波动峰值减小,且从t=0.02 s起管壁速度呈周期性交替变化,交替周期逐渐变小。图12(c)表明注气进入水平段后,管壁速度随着扬程的增加而缓慢减小,交替周期变大,管壁速度逐渐趋于稳定状态。 (3)管壁位移幅值变化 图13为选取的测定A、B和C等测点的注气过程管壁位移幅值随时间的变化情况。结果表明,在持续注入过程中,直井段、井斜段、水平段的油管柱非线性振动幅值与管壁速度变化趋势相似,随着注入流量的增加,各段油管柱幅值变化明显,呈周期性变化。 图13 注气过程管壁位移幅值随时间的变化情况Fig.13 Variation of displacement amplitude of tube wall with time during gas injection 同时图13(a)表明,在注气开启阶段,管壁位移波动幅度较大,从t=0.056 s开始,幅值逐渐稳定在某一区间范围内。由图13(b)和(c)可知,井斜段处管壁速度下降,但位移幅值增加,交变周期较小。表明井斜段形成涡流区,对管壁激振效果明显。且由井斜段(b)向水平段(c)油管柱幅值变化幅度逐渐减小,交变周期变长,笔者判断该现象发生的原因与气体的可压缩性及管壁摩擦阻力有关。在实验的进行过程中,测点(a)和(b)段油管柱发生一定程度震荡,结合前述结果分析表明近注气口段和井斜段是衰竭油气藏储气库井管柱发生非线性振动的高发区域,在管柱安全生产设计和运行时应做出相应的安全措施。 (1) 推导并建立储气库井管柱非线性振动分析方法,以储气库J03-H1井为例,程序实现获得管柱固有特性结果并与有限元模拟结果进行对比,结果表明:储气库井管柱非线性振动分析方法具有良好的适用性;随着管柱设计的增长,环空约束对管柱固有频率影响作用较大;井筒阻尼越大,管柱的共振幅值越小。 (2) 对储气库井管柱进行了瞬态动力学响应分析,证实生产过程,越接近封隔器位置,管柱的振幅、速度和加速度会等振动效果越小,反之效果越大;低频压力波动是生产过程管柱产生振动的重要激励源。 (3) 储气库井管柱非线性振动实验结果可知,随着注气量的增加,各段管柱振动效果变化明显,呈周期性变化。同时,近注气口段和井斜段是储气库井管柱产生振动的高发区域,在管柱安全生产设计和运行时应做出相的安全措施2.4 管柱瞬态动力响应分析


3 储气库井管柱非线性振动实验研究
3.1 实验装置设计
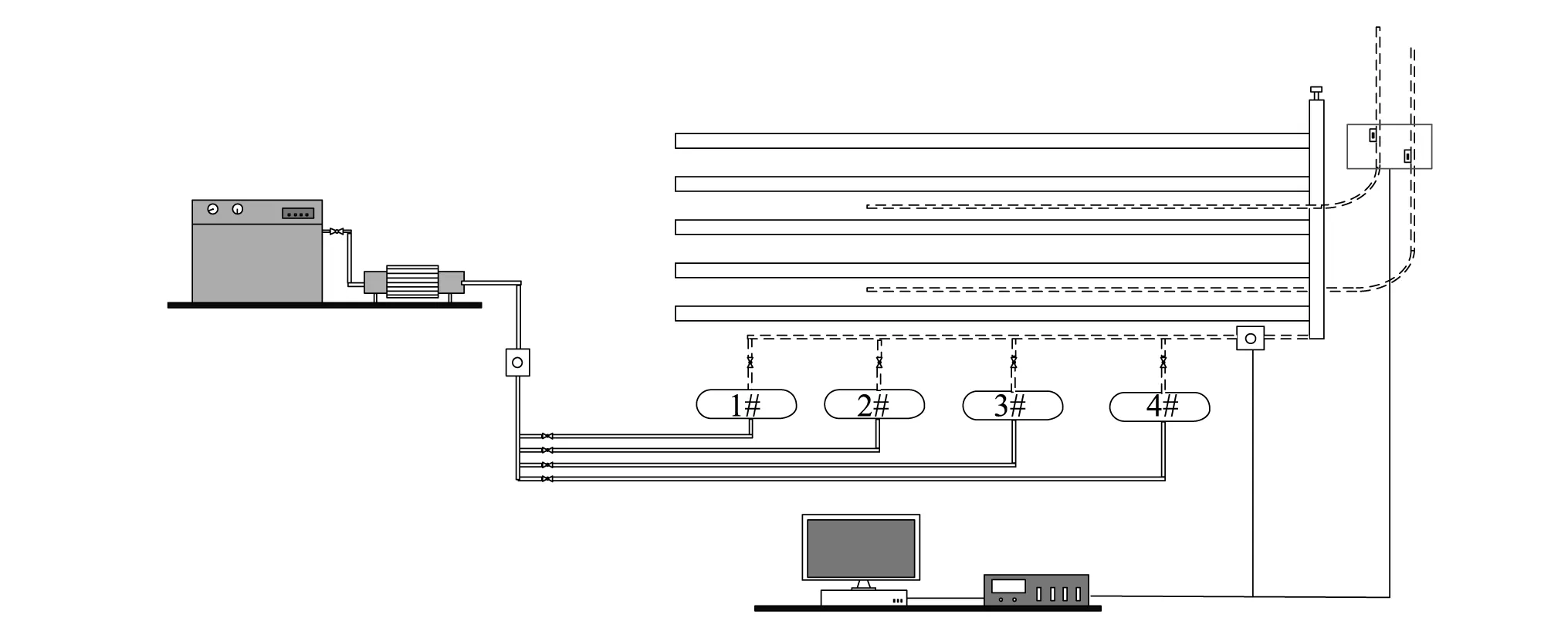



3.2 实验流程
3.3 实验结果分析




5 结 论

