基于非接触转子振动测试的转子行波分析
张岩松, 张东明, 邱大明, 李成刚, 刘 洋
(中国航空发动机集团有限公司 沈阳发动机研究所,沈阳 110015)
航空发动机转子件转动时将产生行波振动,即转子件振动的节径线以某一角速度旋转,即转动方向与转速相同的前行波或相反的后行波振动,行波振动可能造成发动机转子件共振或转静子件碰磨等故障,对发动机造成严重损伤,因而在航空发动机发展过程中进行大量的研究。
在1924年Campbell[1]通过对转子故障研究,提出了行波与固有频率的关系从而建立了Campbell图,而后行波理论被广泛用于发动机零部件振动特性分析中。国内晏砺堂等[2]和吕文林[3]等较早的对行波振动理论和发动机工作状态下叶盘组件行波振动进行了充分的研究论述;晏砺堂等[4]应用声学传感器对齿轮的行波振动信号进行了有效的测试分析,为齿轮破裂故障提供了理论和试验支持;王桂华[5-6]、曹航[7]、洪杰[8]和王能茂[9]等应用不同方法对发动机旋转壳体的行波振动进行了分析;魏武国[10]应用有限元方法对某航空发动机高压压气机盘的行波振动进行了计算分析。从以上研究可以看出,目前国内对于转静子件振动过程中的行波分析进行了较多的研究,研究理论和方法较成熟,但尚未实现航空发动机转子工作过程中的行波振动分析方法。
随着非接触转子振动测试技术的发展,Watkins等[11]介绍了同级转子叶片在静坐标系下测量的振动频率和转子坐标系下测量的振动频率关系可由转速整倍数补偿,但未介绍具体的测试分析方法;Heath等[12-13]在随后进行深入研究,提出叶盘组件的振动节径数可由两支传感器测得叶片振动的相位差确定;胡伟等[14-15]通过试验验证了Zielinski等的理论,采用2支非接触式叶尖定时传感器对发动机转子叶片振动进行测试,通过数据分析确定了转子叶片的行波振动频率和节径数;Kharyton等[16]应用非接触转子叶片振动测试结果分析得到的相位数据特点判定行波方向和振动的节径数。
本文在非接触转子振动测试系统中设计开发了基于离散化傅里叶变换的整级转子叶片振动频率分析模块,实现了整级叶片在静坐标系下的振动频率分析,若转子叶盘发生耦合振动,则分析方法可作为叶盘耦合振动分析的有效方法,在此基础上结合应变计对转子叶片的测试结果首次实现了对发动机转子的行波振动分析。在某型压气机试验过程中,综合分析非接触转子振动测试系统和应变计系统的振动测试结果,得到压气机转子在某一转速段的行波振动特性。
1 非接触转子振动测试原理
基于叶尖定时测量法(Blade Tip-timing)的非接触转子振动测试系统(简称:测试系统)如图1所示。叶尖定时测量法依靠安装在机匣上的叶尖传感器,采集一个转速周期内转子叶片叶尖到达传感器的时间信号,与同一转速周期内转子叶片不振动时叶尖到达传感器的时间信号进行比较,两个时间信号产生时间差,通过对叶尖到达传感器时间差的分析处理,得到叶片振动位移数据,其时间差计算可表示为[17]:
δt=tk-t0,k=1,2,…,Nb
(1)
式中:δt为叶尖到达传感器的时间差;tk为叶片振动时叶尖到达传感器时间;t0为叶片不振动时叶尖到达传感器时间;k为叶片号;Nb为转子叶片数。
由叶片叶尖到达传感器时间差δt,可得测试叶片的周向振动位移计算式为:
d=2πRΩδt
(2)
式中:d为叶片周向振动位移;R为叶片叶尖圆周半径;Ω为转子系统转速频率。

图1 叶尖定时测试系统Fig.1 Typical blade tip-timing system
由测试系统经式(2)所得振动位移为叶片周向振动位移值,叶片实际振动方向与叶片弦线有一定的夹角,其振动位移与测试系统所得的周向振动位移关系如图2所示,图中将叶片在弦向进行投影,则叶片振动位移为[13]:
(3)
式中:dk为叶片振动位移;α为周向振动位移与叶片弦向夹角;β为叶片振动位移与叶片弦向夹角。
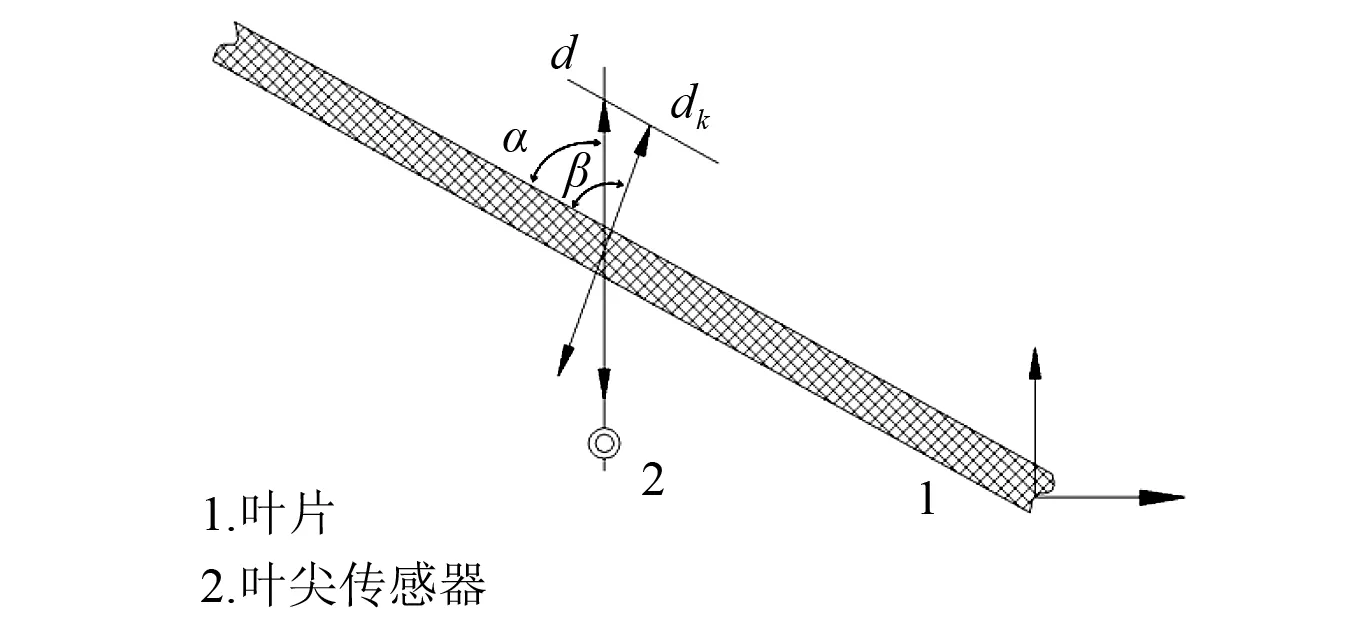
图2 叶片振动位移与测试振动位移关系Fig.2 Conversion of the measuring values in the direction of vibration
测试系统通过采集叶片到达叶尖传感器的时间信号得到转子叶片振动位移数据,若整级转子叶片处于相同频率振动,则静坐标系下的整级转子叶片的振动模式与转速相同的转子坐标系下单个叶片的振动模式相同,因而可对整级转子叶片振动测试数据进行傅里叶变换分析,得到叶片在静坐系下的振动频率。同时测试系统对于整级转子叶片的采样率为叶片数与转速频率乘积。
对于连续时间函数A(t),标准傅里叶变换[11,18]的数据表达式为:

(4)
式中:dt为数据分析的间隔;
将标准傅里叶变换离散化:
(5)
式中:N为离散数据数量;Δt为离散数据间隔;Δf为谱线频率间隔;M为频域内离散谱线数。
对整级叶片振动位移数据进行离散化傅里叶变换,即可得到整级叶片在静坐标系下的振动频率。基于离散化傅里叶变换方法在测试系统中进行程序编制,完成整级叶片振动频率分析程序,基于LABVIEW软件平台开发的分析程序具体如图3所示,图中上半部为分析程序前面板,下半部为分析程序代码。
2 行波振动分析原理
近代发动机压气机盘往往很薄,叶片可能很重,在叶片振动时薄盘与叶片常常产生耦合振动[3]。整级叶片频谱分析理论,假设叶盘组件在运转过程中发生耦合振动[12],其振动模式为节径型振动,即振动位移零点都是沿圆盘面径向分布的直线,这些直线称为节径。以离散化傅里叶变换为基础,通过对整级叶片振动分析,可测定转子叶片静坐标系下的振动频率。发动机旋转件转动时将产生行波振动,在静坐标系下观察前行波与转子件转向具有相同方向,逆行波与转子件转向具有相反方向。

图3 整级叶片振动频率分析程序Fig.3 All blades of the stage spectrum analysis program
转子叶片振动若振幅为Sk,相位为φk,则叶片振动响应为:
(6)
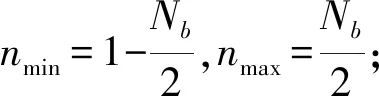
在某一固定激励频率下,以转子坐标系为参考,转子系统振动频率为ωr,则式(6)可变换为:
(7)

在静坐标系下,由于转子件转动使得叶片角向位置发生变化,因此若转子件转速为Ω,则式(7)右侧可变换为:
(8)
对于式(8),转子系统在静坐标系下频率为ωs,则转子系统在静坐标系和转子坐标系下振动频率关系由Watkins等[11]给出其统一形式,即为:
ωs=ωr±nΩ
(9)
测试系统对于整级转子叶片其采样率为叶片数与转速频率的乘积,即未出现频率混叠的最大值,根据采样原理,可知其最大分析频率为通过频率的一半。但是响应频率可能出现多级频率成份,其间隔为转速的整倍数。
3 转子行波振动分析
本文以叶尖定时测量法和离散化傅里叶变换为基础,开发了分析整级转子叶片振动频率的非接触转子振动测试系统,测试系统可应用于航空发动机转子叶片振动测试,为航空发动机工作特性和转子叶片设计、故障诊断和排除等提供试验依据。
采用有限元软件对某压气机叶盘组件单元体扇区进行建模[16,19],如图4所示,对单个叶片进行振动应力分析,根据计算结果确定应变计粘贴位置,应变计方向为径向,如图5所示。从图2和图5所示可看出,测试系统测得的振动位移和应变计测量的振动应力为同一振动方向的响应,则测试结果统一,可对叶片振动特性进行综合分析。

图4 叶盘组件 有限元模型Fig.4 The finite element model of blade-disk

图5 应变计粘贴位置Fig.5 The location of Strain gage
在压气机叶盘组件工作时综合考虑转速和气动载荷因素进行耦合振动分析,由有限元软件ANSYS计算结果表明叶盘组件在地面试车存在4节径一阶耦合振动模态,叶盘耦合振动频率为933.4 Hz,如图6所示,图中不同颜色表示组件不同部位的振动相位,为使振动节径数较明显,对叶片振动位移值的标尺进行设置。
在压气机试验过程中,在叶片上安装应变计的同时机匣上安装非接触式叶尖定时测试传感器,非接触式叶尖定时测试传感器安装周向位置如图7所示,从整级转子叶片具有相同振动频率的特点,可知不同叶片在经过传感器时的振动位移即为转子坐标系下单个叶片不同相位时的振动位移;应变计周向分布如图8所示,应变计对称分布,每侧连续七个叶片粘贴应变计。

图6 叶盘耦合振动分析结果Fig.6 The analysis of blade-disk vibration

图7 叶尖定时测试传感器安装周向位置Fig.7 Blade tip timing probe mounted on the casing-circumferential position

图8 粘贴应变计叶片装配位置Fig.8 Blades of install strain gage assembly position
对应变计测试结果进行分析,在压气机某一转速段工作时转子叶片出现明显振动,所有叶片振动频率保持在926.4 Hz(平均值)左右,随机选取其中某一叶片进行频谱分析如图9所示,全部叶片的应变计振动频率测试结果,如表1所示。

图9 单个叶片应变计振动频率分析Fig.9 One blade spectrum of strain gage measurement

应变计号Ω/(r·min-1)ωr/Hz应变片号Ω/(r·min-1)ωr/Hz112 343926.6812 343926.6212 343926.5912 343926.4312 343926.31012 343926.3412 343926.71112 343926.2512 343926.61212 343926.1612 343926.11312 343926.1712 343926.81412 343926.7
从测试结果可以看出,粘贴应变计的叶片的振动频率基本相同,则可判定整级转子叶片在转子坐标系下具有相同的振动频率。
选取相同稳态转速段,对测试系统的整级转子叶片振动测试结果进行分析,整级叶片出现明显的振动,分析结果如图10所示,图中A部为某一单个转子叶片全转速范围内振动情况,图中B部为图中A部选定转速段内整级叶片振动情况,图中C部为整级叶片振动局部图,图中D部为某一转速周期内不同叶片振动位移图,图中E部为整级叶片振动频率分析结果,整级叶片振动频率值在图中圈中示出。

图10 整级叶片振动频率分析Fig.10 All blades of the stage spectrum analysis
测试系统分析结果为叶盘组件在静态坐标系下的耦合振动频率,应变计测得结果为叶盘组件在转子坐标系下的耦合振动频率,将试验测试结果代入式(9)可得叶盘组件在工作过程中行波振动的节径数,结果,如表2所示。

表2 整级叶片行波振动分析结果Tab.2 Traveling vibration result of the stage all blades
表2中行波节径数测试计算结果的误差在可接受范围内,其出现的主要原因是由于测试误差造成[20-21]。从测试数据分析结果中可以看出,压气机叶盘转子组件在转速12 343 r/min左右工作时将出现4节径前行波振动。航空发动机转子件的设计应重点关注2、3、4节径的振动,此种振动对转子件造成损坏的可能性较大,直接影响发动机及飞机的安全性。压气机转子后行波振动频率可由式(9)计算得到。
将压气机转子动频及行波振动频率在静坐标系下进行分析,得到压气机转子振动的Campbell图,如图11所示。

图11 压气机转子振动坎贝尔图Fig.11 Campbell diagram for rotor of compressor
从图11中可以对发动机工作特性进行预测,发动机转子振动在最高工作转速工作时具有较小的频率裕度和转速裕度。
从以上分析结果可以看出,本文综合运用非接触转子振动测试系统和应变计振动测试结果,可准确判定发动机某级转子在工作过程中的行波振动特性,改善了以往应用静频和应变计测试结果进行发动机转子行波振动分析的传统方法,可广泛应用于工程实践中。
4 结 论
本文以叶尖定时测量法和离散化傅里叶变换为理论基础,建立了非接触转子振动测试系统,形成了整级转子叶片在静坐标系下的振动频率分析方法,结合应变计在转子坐标系下对转子叶片振动频率的测试结果,在实际测试中实现了航空发动机转子的行波振动分析。
在某型号压气机测试过程中,应用整级转子叶片振动频率分析方法,结合应变计测试结果,实现了转子叶片静坐标系下和转子坐标系下振动频率的同时测量,应用行波振动理论得到压气机转子行波振动的节径数。本文的研究为航空发动机转子行波振动分析提供了一种准确的测试手段,测试结果可为发动机转子件设计和工作特性分析提供参考,同时可为发动机的故障诊断和排除提供有力的技术支持。

