内装电磁滑环式主动平衡系统的研究

潘 鑫， 何啸天， 吴海琦， 高金吉， 江志农

(1. 北京化工大学 发动机健康监控及网络化教育部重点实验室，北京 100029；2. 北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室，北京 100029)

近年来，国内外已经研制了多种类型的主动平衡系统，主要包括电磁轴承式[4]，液体式[5]，电机式[6]和电磁滑环式等。其中，由于电磁滑环式平衡执行器具有响应速度快、精度高、结构紧凑等多项优点，更适于集成到机床主轴上。该结构是利用电磁力驱动配重块旋转、进而在线改变自身质量分布的主动式平衡执行器，由Dyer等[7]首先提出。之后，Shin等[8]针对该类执行器的自适应控制算法进行了研究；Moon等[9]在卧式加工中心上对该执行器进行了自动平衡实验。目前已有德国Hofmann、意大利MARPOSS和美国SBS等多个厂家将其开发为商业产品[10-11]。西安交通大学和北京化工大学等高校和科研院所也对该执行器进行了深入研究[12-15]。然而，目前已报道的电磁滑环式平衡执行器均仅可以穿轴安装的方式安装在被测转子外部，通常安装在主轴转子外伸段的根部，需要占用主轴的部分加工空间。如果平衡执行器可安装在转子的内部，则更有利于智能主轴的集成，亦可扩展该执行器的工程应用范围。因此，为解决上述问题，本文介绍一种可内装于机床主轴上的新型电磁滑环式主动平衡系统，对其中执行器的部分性能参数进行了定量分析，并完成了相关实验验证。

1 平衡系统工作原理

内装电磁滑环式主动平衡系统主要由传感器、数采单元、控制单元、供电单元和执行器等几部分组成，如图1所示。该系统的工作原理如下：利用振动传感器实时在线监测机床主轴的振动，所获得的振动信号通过数采单元的模拟输入模块实时同步传输至控制单元；控制单元内嵌监控软件，可持续监测分析主轴的不平衡振动参数，并将实测值与设定值进行对比分析；当主轴的不平衡振动幅值高于设定值时，控制单元根据所测不平衡振动参数形成控制命令，并通过数据采集单元的I / O模块将其发送到供电单元；供电单元根据控制指令形成相应电信号，并通过线缆将电信号输出至平衡执行器；平衡执行器预先安装在机床主轴内部，可根据电信号在线改变自身的质量分布，产生补偿质量以在线抑制主轴转子的不平衡振动；当不平衡振动的幅度再次低于设定值后，控制单元停止输出控制指令，平衡过程结束。

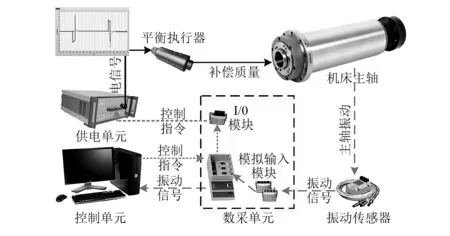
图1 平衡系统的原理示意图Fig.1 Working principle of the balancing system

2 平衡执行器

平衡执行器是主动平衡系统的终端执行器，其性能决定了平衡系统的最终效果，因此有关执行器的设计是主动平衡技术研究的核心内容之一。

2.1 结构设计

如图2所示，平衡执行器包括动环和静环两部分。其中，动环与中空转子同步旋转，并通过自身质量分布的改变产生补偿质量，在线抑制转子的不平衡振动；静环在工作过程中保持静止，从供电单元接收电信号并产生交变磁场以驱动动环动作。静环由两个线圈及相应外壳、一个中心定子和若干螺母组成。其中，中心定子加工有通孔，用于供电单元与两个线圈间的布线。动环包括执行器外壳、两个端盖、四个铁齿环、两个带配重块的配重盘、两个球轴承等。执行器外壳用于连接执行器与主轴的中空转子，并可根据转子内孔的尺寸进行定制设计。动环的其他部件成对对称分布，且均与执行器外壳相连。其中，四个铁齿环可分成两对，每对包含一个外铁磁环和一个内铁磁环，具体工作原理见下节。两内铁磁环中心加工有通孔，用于连接中心定子。由于动环的内铁磁环与静环的中心定子在运行期间有相对运动，因此采用一对球轴承用于保证执行器的长周期运行[16]。

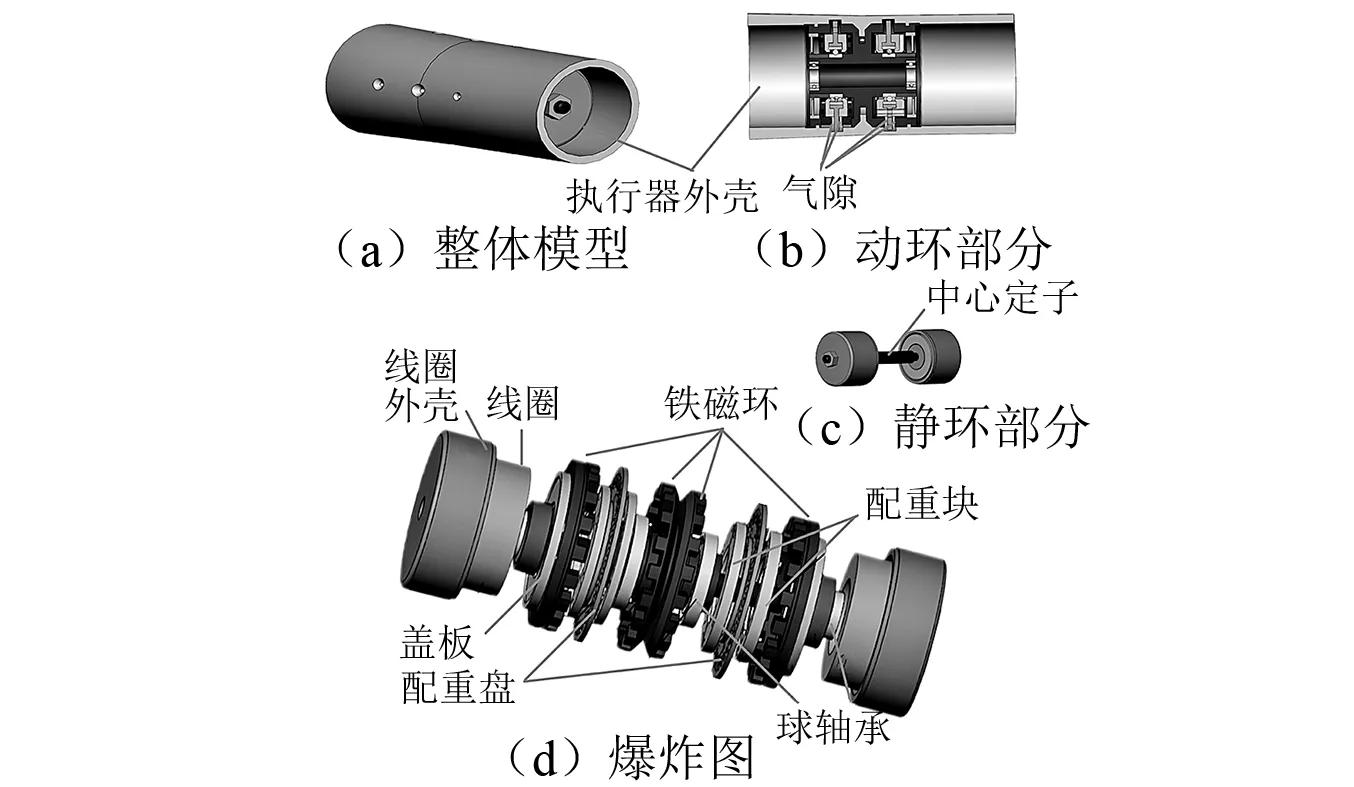
图2 平衡执行器三维模型Fig.2 Three-dimensional model of the balancing actuator

2.2 步进旋转原理

在该类平衡执行器中，设计核心之一为如何控制配重盘的运动，即无需工作的时候，要求该部件能随被测转子与动环同步旋转，且在接收指令后，又能相对动环进行步进旋转，以产生补偿质量。

如图3所示，配重盘的外圆周上装有等间距的永久磁铁，且相邻永久磁铁的极性相反，用于实现配重盘自锁和外部磁场驱动；铁磁环为轴向凸起的齿形结构，且齿形轮廓为矩形，齿宽为相邻两永磁体的间距，齿宽为两圈永磁体的内外径之差。配重盘两侧以螺栓紧固的方式镶嵌两配重块，用于作为偏心质量。

无控制指令时，配重盘处于自锁状态，如图3(a)所示，在该自锁力作用下，配重盘随动环以及被测转子同步旋转，平衡执行器的质量分布不发生变化。当线圈通电后，配重盘两侧的铁磁环被快速磁化。以逆时针旋转的情况为例，两个铁磁环分别被磁化为N极和S极，配重盘在磁力驱动下相对于磁化的铁磁环步进旋转，如图3(b)所示。当配重盘移动到图3(c)所示中间位置时，配重盘的角速度达到最大值。此时，线圈断电，磁场消失。在自锁力作用下，配重盘逐渐减速并在图3(d)所示的位置停止步进。通过一步的步进旋转，配重盘相对于执行器旋转一个固定角度。如果需要配重盘继续前进，则需要在线圈上施加反向电压，进而使铁磁环产生反向磁场，如图3(e)所示。

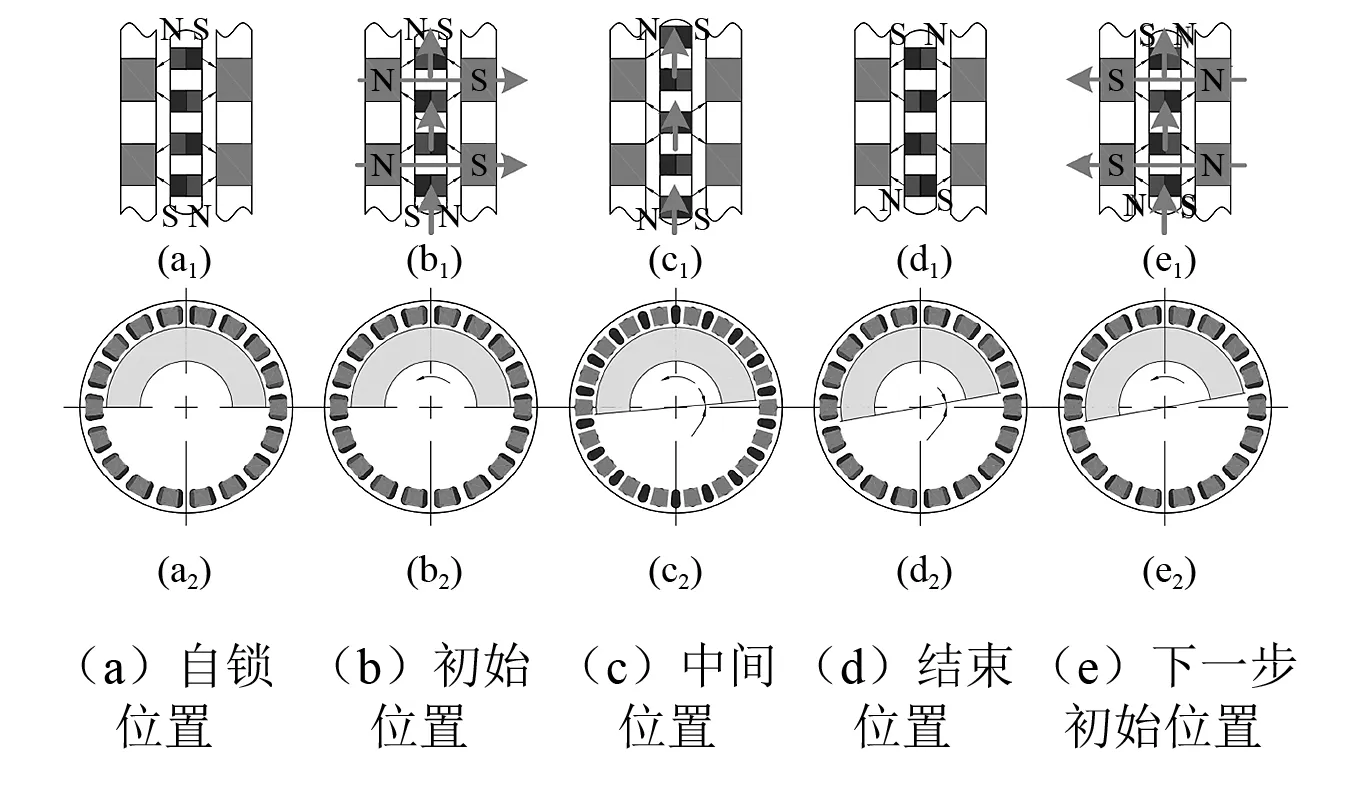
图3 配重盘的运动过程Fig.3 Step rotary process of the balancing actuator

2.3 在线平衡原理

平衡执行器自身的质量分布主要由两个配重盘的相对位置来决定。如图4所示，每个配重盘的两侧均安装有一对半圆形的偏心配重块，每个配重盘所形成的偏心质量分别用UA和UB表示。当执行器预先安装在主轴转子内部时，两个配重盘的配重块位于相反的方向，因此UA和UB相互抵消，所形成补偿质量为零，为平衡执行器的初始状态，如图4(b)所示。在平衡过程中，UA和UB之间的角度通过两个配重盘的步进旋转而逐渐减小，所形成的补偿质量随之逐渐增加。当两个盘的配重块在同一方向时，UA和UB叠加，补偿质量达到最大值，该值即被称为执行器的最大平衡能力。

除了在设计上体现古代学院的教育智慧和教育理想，史家书院还处处体现着古代书院具有的思想自由、有教无类的活跃氛围，史家书院“传统文化小主讲”活动正是传承了中国古代书院的“讲会”制度。热爱中国传统文化的孩子可以主动报名到书院做“小主讲”，并邀请父母、老师和专业人士做助教，讲授内容包罗万象，可以是古代乐器、古代机械、文房四宝或是青铜器。低年级的弟弟妹妹可以给高年级的哥哥姐姐上课，有时候连老师都会跑来“蹭”课。现在“传统文化小主讲”活动已经固定为史家小学的校本课程，书院文化在同伴分享的过程中变得更加鲜活、生动。

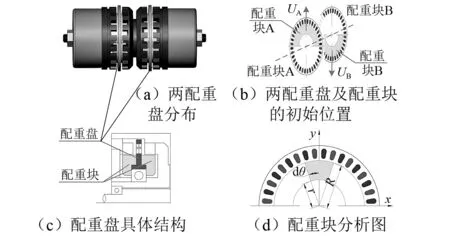
图4 配重盘结构图Fig.4 Structure drawing of counterweight disc

3 性能分析

3.1 平衡精度

由在线平衡原理知，当执行器预装在转子内部时，两个配重盘的配重块处于相反的方向，初始补偿质量为零；在平衡过程中，通过两个配重盘的步进旋转，逐渐产生补偿质量。为分析执行器的平衡精度，首先考虑步进旋转过程。

假设配重盘上的磁铁数量为N，则每一步旋转的中心角Δφ等于360/N。当补偿质量从0增加到最大值时，两个配重盘有三种旋转方式：

(1)两个配重盘同时接近对称轴并每次旋转一步。 在该过程中，总步长为N/ 4，补偿矢量U和补偿矢量ΔU的变化可表示为：

(1)

式中：UAB为单个配重盘的平衡能力；φA和φB分别为配重盘A和配重盘B的初始相位，对应数值分别为0，和180°。

(2)两个配重盘依次接近对称轴并每次步进旋转一步。总步数为N/ 2，补偿矢量U和补偿矢量ΔU的变化表示为：

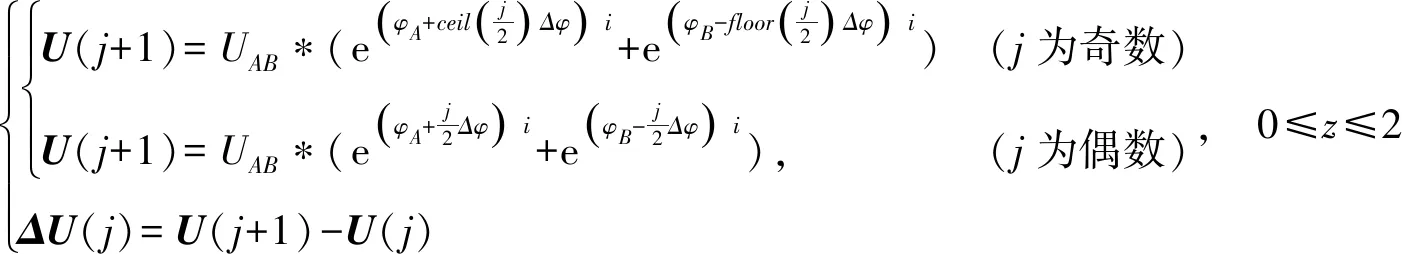
(2)

(3)一个配重盘保持静止，而另一个配重盘逐渐接近另一侧。总步数也是N/ 2，两向量表示为：

(3)

对于实验验证中所用执行器，每个配重盘UAB的平衡能力为584 g·mm，磁铁的数量N为36。三种步进旋转方法的计算结果，如图5所示。

由图5可知：①后两种旋转方法的补偿矢量的变化量是一个固定值，即任何位置每一步的ΔU总是50.9 g.mm；②对于第一种旋转方法，ΔU从101.4 g.mm减小到8.9 g.mm，即当两个配重盘之间的相位差大于90°时，第一种方法的平衡精度不如后两种方法的平衡精度，但当相位差小于90°时，第一种方法的平衡精度更好。在执行器的实际控制过程中，应结合三种方法，补偿矢量的变化范围在[8.9, 50.9]范围内。由于平衡精度是指执行器在每次步进平衡过程中均能达到的最小数值，因此，本文所设计执行器的最终平衡精度数值为50.9 g·mm。

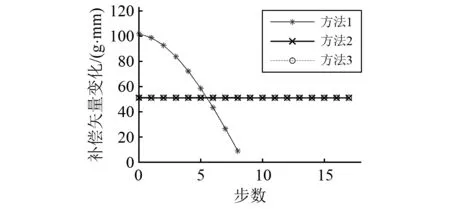
图5 平衡精度分析结果Fig.5 Diagram of balancing accuracy analysis

3.2 自锁能力

由2.2节步进旋转原理所示，平衡执行器正常处于自锁状态，自锁力矩由永磁体和铁磁环间相互作用的磁力产生，使得配重盘与平衡执行器同步旋转。因此，必须保证平衡执行器具有足够的自锁能力，以防止配重盘在未接到控制指令时出现误动作。由于该执行器是轴对称结构，且自锁能力仅与配重盘上的永磁体及左右铁磁环相关，因此，本文以一个配重盘和左右铁磁环为分析对象，基于Maxwell软件建立这三个部件的有限元模型和部分分析结果，如图6所示。

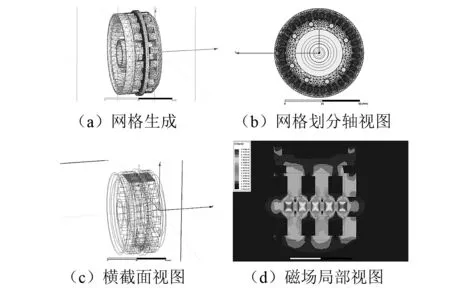
图6 自锁力矩有限元分析Fig.6 Finite element analysis of self-lock torque

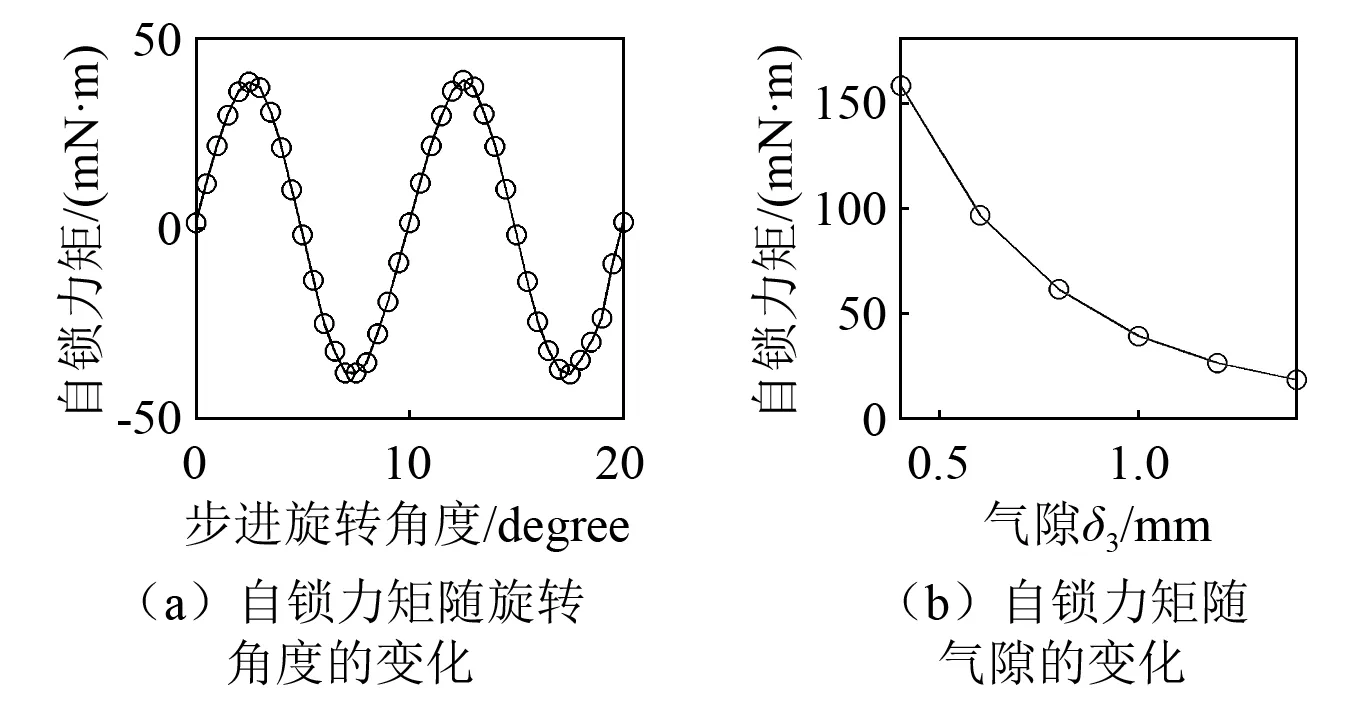
图7 自锁力矩分析结果Fig.7 Analysis results of self-lock torque

由图7所示的分析结果可知：①自锁力矩的变化周期与两相邻磁铁间的中心角相等，并在步进过程中，最大力矩值出现在1/4和3/4步的位置；②随着配重盘与左右铁磁环间气隙δ3的增大，自锁力矩迅速减小，当气隙为1.0 mm时，自锁力矩为38.9 mN·m。

由配重盘的受力分析知，自锁力矩MT与执行器的启动加速度αn的对应关系可表示为

(4)

式中：m为配重块的偏心质量；J为配重盘的转动惯量。经计算知，当配重盘和铁磁环的气隙为1.0 mm时，要求执行器的启动加速度要低于353 rad/s2，即当被测转子的工作转速为3 600 r/min时，设备的启动时间长于1.1 s，执行器即可正常工作。

4 实验验证

为验证上述主动平衡系统的有效性，搭建相关实验台进行实验验证，实验装置如图8所示。

图8 实验装置总体图Fig.8 Overall diagram of experimental device

该实验台采用西门子步进电机驱动具有中空转子的机床主轴。平衡执行器安装在该主轴的空心转子中，使用Bently3300位移传感器在线监测转子系统的振动。数采单元为包含两个数据采集模块和一个数字输出模块的cDAQ数采器，其中两数据采集模块用于测量振动信号、转速信号和配重盘定位信号，数字输出模块用于输出控制指令。采用PC台式机作为控制单元，用于实时分析转子系统的振动信号，并计算转子系统的初始不平衡以及生成控制指令。执行器如图9所示。其最大直径为66 mm，总长度为110 mm，最大平衡能力为1 160 g.mm。选择两个350 W/15 V 直流电源为执行器供电。由实验调试结果知，该执行器可以在15～18 V下正常工作，且当供电电压为18 V，脉冲宽度可在24 ms到30 ms之间进行选择。

主动平衡实验所用转速为3 600 r/min, 实验结果如图10所示。由该图知，设备的初始不平衡振幅为3.2 μm，经过主动平衡，可在20 s内将该幅值降低至0.4 μm以下，振动降低幅度达87.5%。设备的初始不平衡振动相位为140度；在平衡过程中，振动相位稍有变化，变化范围为40度；平衡过程结束时，由于此时的不平衡振动幅值已经很小，以至于振动相位发生了大范围的波动。由于该波动主要受实验装置本身精度的影响，因此平衡程序终止，平衡过程结束。

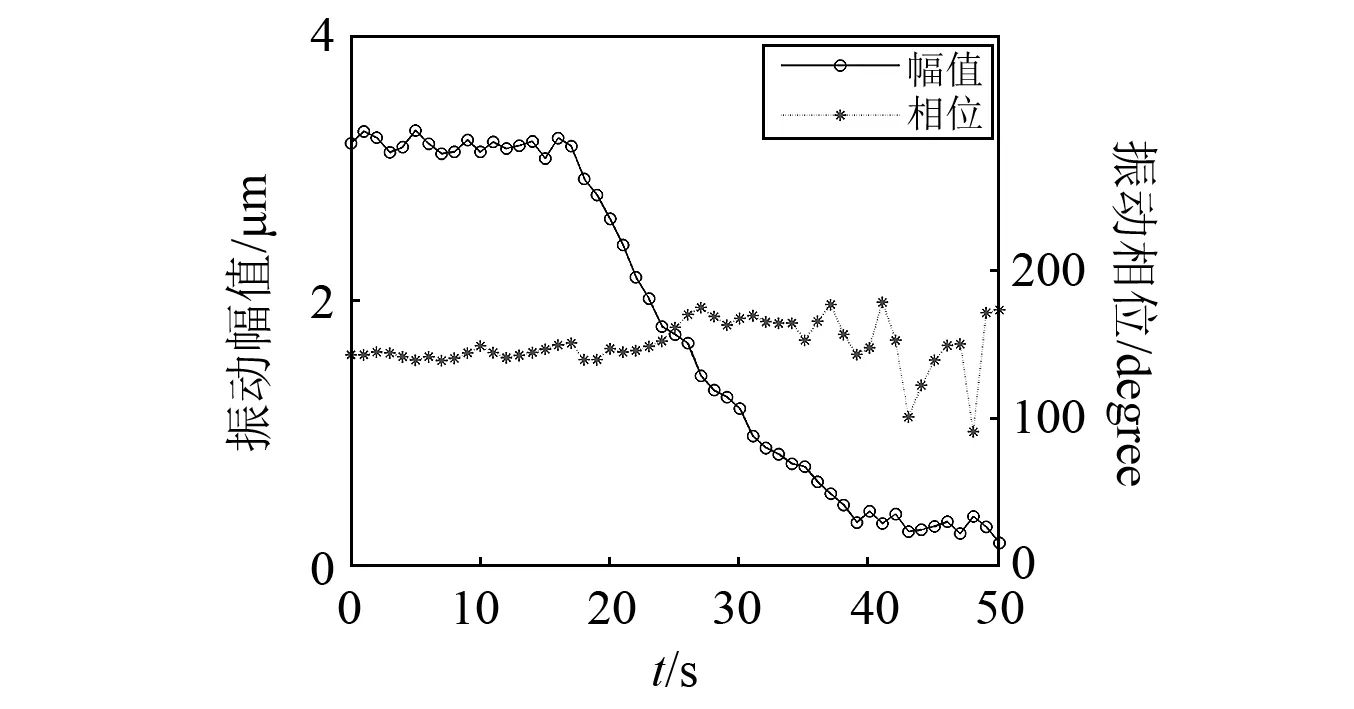
图10 主动平衡实验效果Fig.10 Active balancing experiment results

5 结 论

本文介绍了一种可集成在机床主轴中空转子内部的新型电磁滑环式主动平衡系统。在介绍了该系统基本工作原理的基础上，重点介绍了平衡执行器的相关结构以及步进旋转和在线平衡的相关工作原理，对执行器的平衡精度和自锁能力两项指标进行了定量分析。最终，在3 600 r/min的转速下通过自动平衡实验验证了该主动平衡系统的有效性。实验结果表明，该主动平衡系统可在20 s内将机床主轴的不平衡振动从3.2 μm降低至0.4 μm以下，振动幅值减少87.5%。

在今后的研究中，拟将该主动平衡系统应用于实际机床上，以验证该系统在提高机床主轴加工精度和效率方面的作用。随着智能主轴和工业4.0技术的发展，主动平衡系统将具有更广阔的市场前景。