随机地震作用下TMD等效附加阻尼比研究
贺 辉, 谭 平, 林松伟, 向 越, 兰 李
(1. 湖南工学院 土木与建筑工程学院, 湖南 衡阳 421002;2. 广州大学 土木工程学院, 广州 510006; 3. 广东省建筑设计研究院有限公司, 广州 510405)
调谐质量阻尼器(tuned mass damper, TMD)作为一种被动控制装置,已被广泛应用于高层高耸结构[1]。一般情况下,TMD由质量块、弹簧以及阻尼元件组成[2]。高耸高层结构安装TMD,主要是为了增加结构的阻尼,达到控制结构振动的目的[3]。TMD控制效果越好,结构增加的阻尼也就越大,结构增加的这部分阻尼比被称为TMD等效附加阻尼比[4]。1977年,McNamara 基于高斯白噪声外激励以结构位移响应均方值相等为准则推导了TMD等效附加阻尼比理论公式[5]。Luft以TMD等效附加阻尼比最大作为优化条件给出了TMD最优设计参数[6]。王肇民以电视塔结构作为工程背景,给出了风荷载作用下TMD给结构第一阶模态的等效附加阻尼比理论公式[7]。
目前,应用TMD来控制结构的风振响应已经得到了人们的广泛认可[8],但是地震作用下TMD的有效性还没有统一的定论[9-10]。已有研究表明,TMD的减震性能很大程度上取决于地震动特性[11-13]。Villaverde等人假定结构-TMD体系前两阶模态阻尼比相等给出了地震作用下TMD等效附加阻尼比公式[14]。然而,文献[14]给出的TMD等效附加阻尼比公式仅在TMD频率比等于1且TMD阻尼比满足一定条件的情况下成立[15]。更重要的是,它忽略了地震动特性对TMD等效附加阻尼比的影响,因此其计算精度有待验证。鉴于此,有必要考虑地震动特性对TMD等效附加阻尼比进行更深入地研究。事实上,以往的TMD等效附加阻尼比研究多数是基于单自由度主结构展开,仅能得到TMD提供给结构第一阶模态的附加阻尼比,无法准确评估TMD提供给结构高阶模态的等效附加阻尼比。
在此背景下,本文将基于考虑场地因素的过滤高斯白噪声Kanai-Tajimi功率谱模型,推导出一个能准确评估随机地震作用下TMD提供给结构任意阶模态的等效附加阻尼比理论公式。本文将从结构-TMD理论模型、结构随机地震响应分析以及TMD等效附加阻尼比理论公式推导等方面逐一展开研究。
1 结构-TMD理论模型
假定结构有n个自由度,且TMD与第n个自由度相连,可将结构-TMD体系表示为图1所示的理论模型。图1中:mn、kn和cn分别表示结构第n个自由度的质量、刚度与阻尼系数;mt、kt和ct分别表示TMD质量、刚度和阻尼系数;xn表示结构第n个自由度相对于地面的位移,xt为TMD相对于结构第n个自由度的位移。
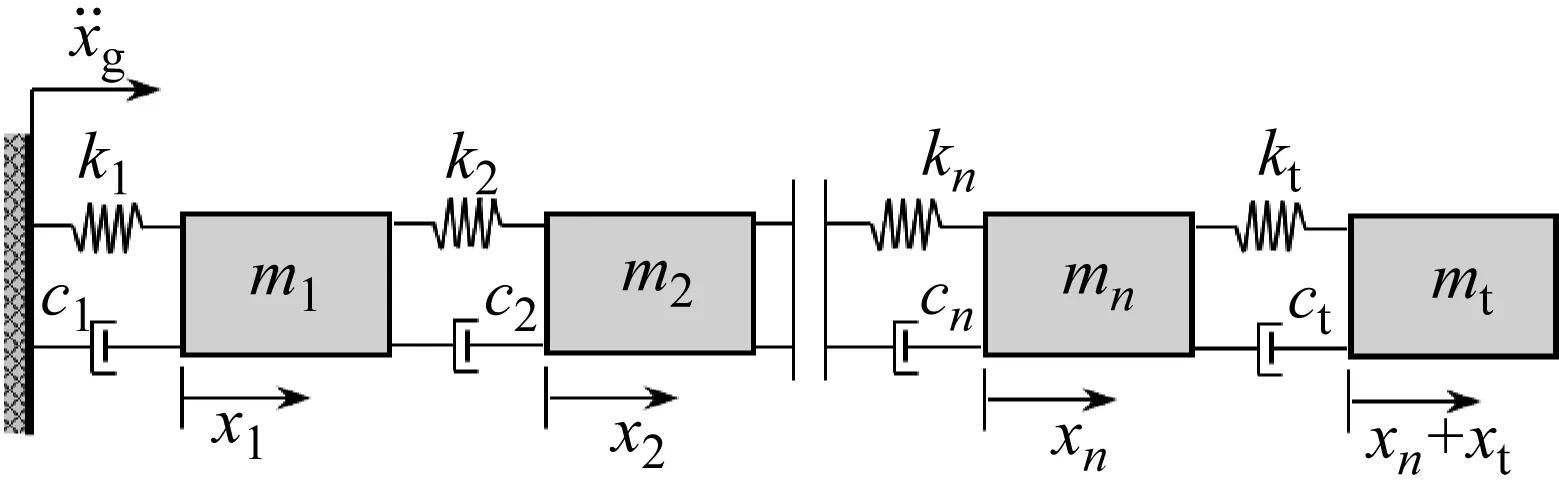
图1 结构-TMD理论模型Fig.1 Theoretical models
{FTMD}
(1)
式中
(2)
(3)
结构阻尼矩阵采用Caughey阻尼矩阵,TMD对结构的作用力可表示为
(4)
TMD运动方程为
(5)
将TMD看作一个子结构,忽略TMD对主结构自振特性的影响,此时将主结构进行模态分解,考虑结构第j阶模态φj时,引入表1所示的系统参数。

表1 系统参数定义
进一步可将结构-TMD体系的模态运动方程表示为
(6)
式中,uj表示结构第j阶模态广义坐标,此时

(7)

Hj(iλj)=
(8)
其中
(9a)

(9b)
2 结构随机地震响应分析
地震动功率谱模型采用Kanai和Tajimi等提出的过滤白噪声模型,其加速度功率谱密度函数为[16-17]
(10)
式中:S0为基岩白噪声强度;ωg和ζg分别表示场地特征频率与特征阻尼比;ωg和ζg的取值可通过实际地震记录拟合得到,也可由表2直接确定。

表2 场地土参数设计值[18-19]
Kanai-Tajimi功率谱模型将场地视为单自由度线性滤波器,由基岩白噪声通过土层过滤得到,由此可将场地的过滤效应表示成传递函数形式
(11)
将ω=λjωj代入式(11),可得
(12)
式中,主结构第j阶模态频率与场地特征频率比τj=ωj/ωg。进一步将土层看作一个与上部结构串联的系统,由此可得结构相对于基岩白噪声的位移动力放大系数为
Hg,j(iλj)=H(iλj)H′(λj)=
(13)
式中
(14a)
(14b)
采用SRSS方法计算地震作用下结构的位移响应均方值
(15)
其中
(16)
式中
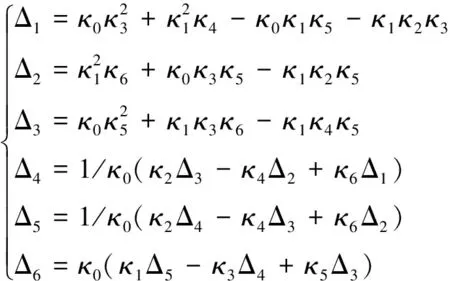
(17)
3 TMD等效附加阻尼比
将结构-TMD体系等效为一个第j阶模态阻尼比为ζe,j的等效结构,类似地,可将等效结构相对于基岩白噪声的位移动力放大系数表示为
(18)
式中

(19)
等效结构位移响应均方值可表示为
(20)
其中
(21)
(22)
整理得
(23)
其中

(24)
则TMD提供给结构第j阶模态的等效附加阻尼比理论公式为

(25)
其中
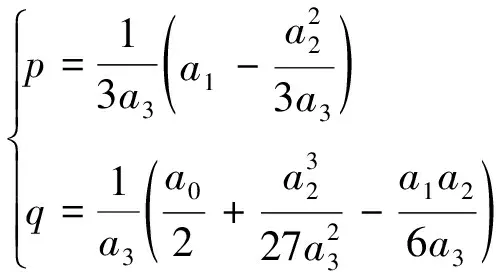
(26)
为了对式(25)的有效性进行验证,定义以下三种TMD等效附加阻尼比计算方法:
方法一:使用本文所提理论公式计算TMD等效附加阻尼比;
方法二:使用文献[5]的TMD等效附加阻尼比公式
(27)
方法三:使用文献[14]的TMD等效附加阻尼比公式
(28)
事实上,ζs2,j与ζs3,j均是基于单自由度主结构推导而来,无法得到TMD提供给结构高阶模态的等效附加阻尼比,因此方法二与方法三仅考虑TMD对结构第1阶模态阻尼比的影响。
4 参数分析
考虑结构第一阶模态(j=1),令φ1,n=1和η1=1,假定TMD频率比与阻尼比采用Den Hartog公式[20],对ζs1,1进行如图2所示参数分析。由图2可以观察到以下现象:
(1) 结构与场地特征频率比τ1小于等于1时,特征阻尼比ζg越小,TMD等效附加阻尼比ζs1,1越大。然而,当τ1>1时,随着ζg增大,ζs1,1却会变小;
(2) 当τ1≤1时,τ1对ζs1,1的影响相对较小。但是,当τ1>1时,τ1的增大会使ζs1,1迅速变小;
(3)ζs1,1与结构阻尼比ζ1呈负相关关系;
(4) TMD质量比μ1存在一个临界值|μ|,当μ1≤|μ|时,随着μ1增大,ζs1,1会随之增大。当μ1>|μ|时,随着μ1增大,ζs1,1会迅速减小。值得一提的是,随着μ1增大,ζs1,1可能会小于0。也就是说, TMD质量比太大可能会放大结构响应。
为了进一步研究地震动特性对TMD等效附加阻尼比的影响规律,令ζ1=0以及ζg=0.80,将TMD等效附加阻尼比进行如图3所示的对比分析。从图3中可以看出:
(1) TMD质量比μ1小于1%时,三种方法计算出来的TMD等效附加阻尼比ζs,1基本一致;
(2) 方法二得到的TMD等效附加阻尼比大于方法一与方法三,这是由于方法二的TMD等效附加阻尼比公式是基于外荷载激励形式推导而来,无法适用于地震作用下TMD等效附加阻尼比的计算。这一现象也说明相对于结构地震响应控制而言,TMD更有利于控制结构的风振响应。
(3) 方法二与方法三得到的TMD等效附加阻尼比与TMD质量比μ1成正相关关系,不存在一个临界值|μ|,因此随着TMD质量比μ1的增大,与方法一会存在很大的差异。
(4) 当τ1较小时(如τ1=1),方法一与方法三的计算结果相近。但是,当τ1较大时(如τ1=10),随着μ1的增大,方法一与方法三计算结果的差距也会越来越大,且方法三计算出来的TMD等效附加阻尼比偏大。这是因为方法三忽略了地震动特性对TMD等效附加阻尼比的影响,导致计算过程中夸大了TMD提供给结构的等效附加阻尼比。
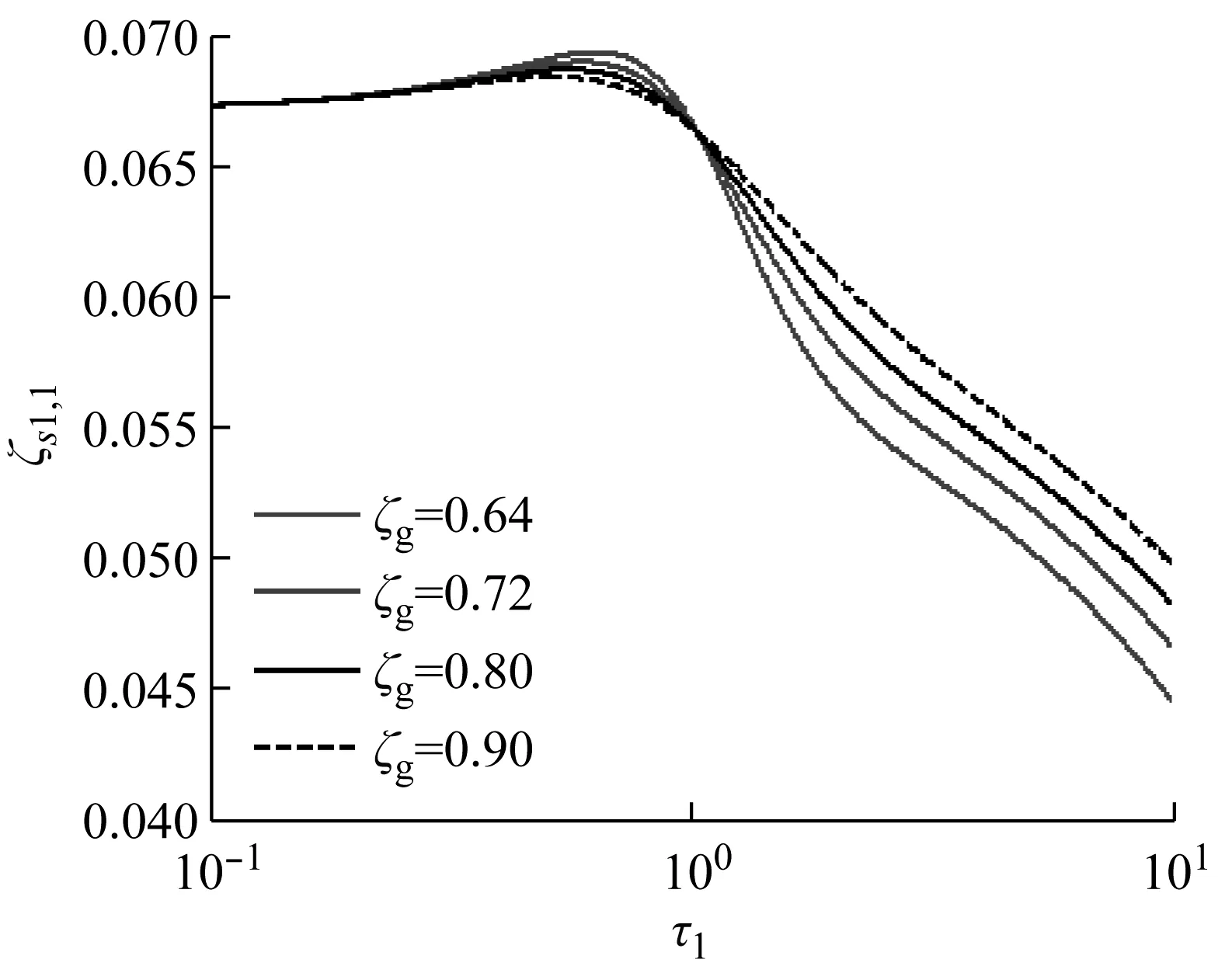
(a) μ1=0.1,ζ1=0
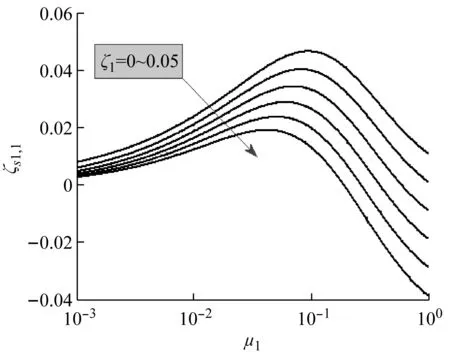
(b) τ1=10,ζg=0.80图2 TMD等效附加阻尼比分析Fig.2 Analysis results of the equivalent additional damping ratio of TMD
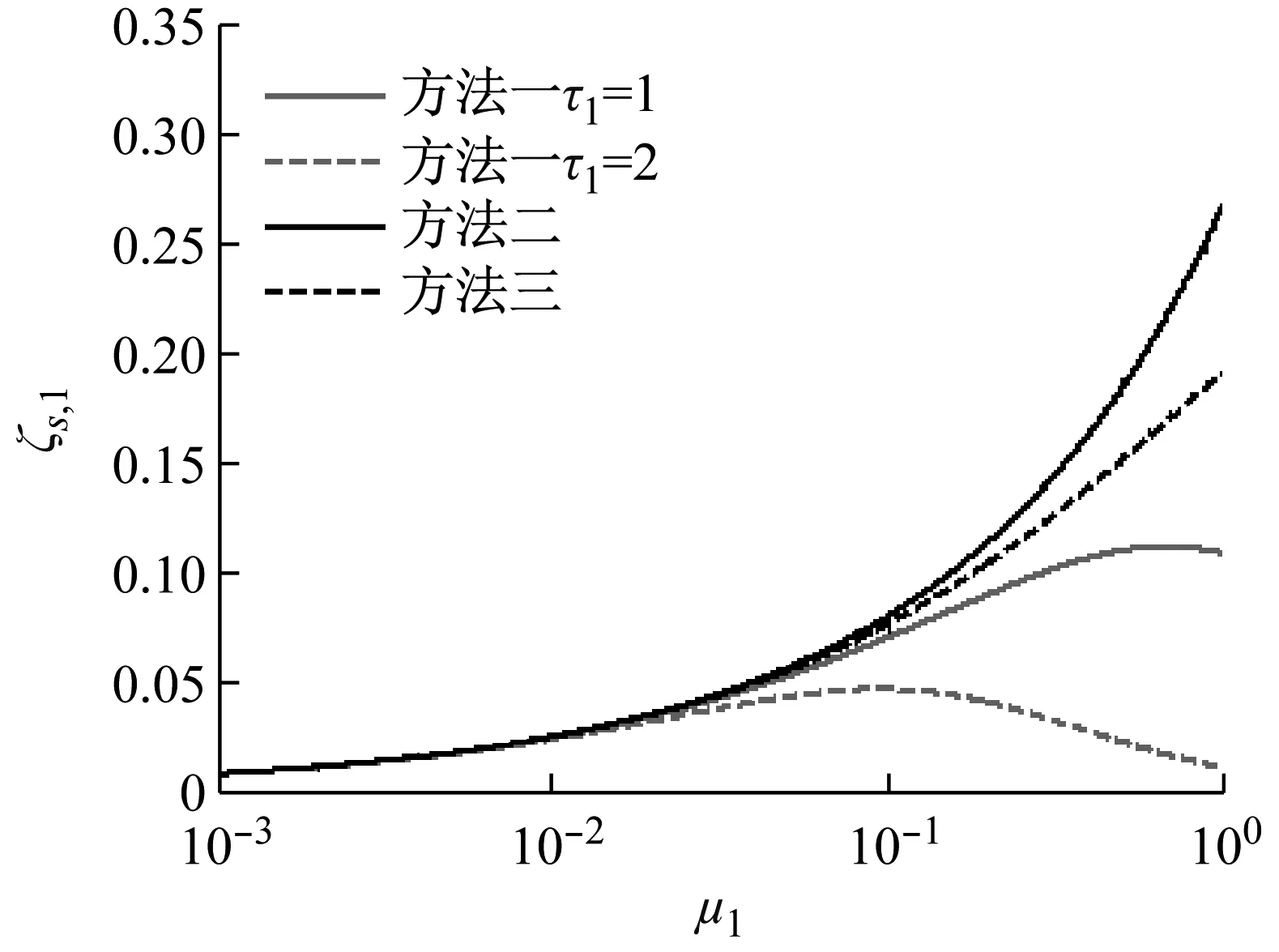
图3 TMD等效附加阻尼比对比分析Fig.3 Comparison analysis results of the equivalent additional damping ratio of TMD
为了对上述现象进行更深入地研究,对结构位移放大系数进行分析。方法三假定结构-TMD体系前两阶模态阻尼比一致,本质上是直接从结构相对于地面的位移放大系数H1(iλ1)出发求解TMD等效附加阻尼比。而本文则考虑场地土对地震动频谱特性的影响,给出了结构相对于基岩的位移放大系数Hg,1(iλ1)。对比图4与图5(a)可知,当τ1较小时(如τ1=1),H1(iλ1)与Hg,1(iλ1)的变化规律基本一致,TMD质量比增大,二者的峰值均变小。
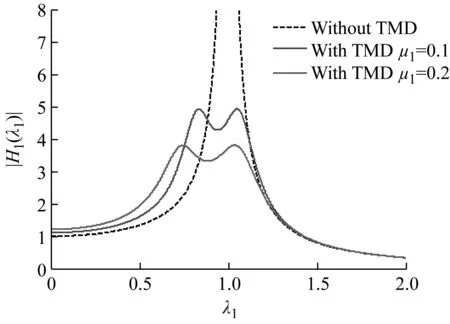
图4 主结构相对于地面的位移动力放大系数Fig.4 Analysis results of the displacement dynamic amplification factor of structure to ground
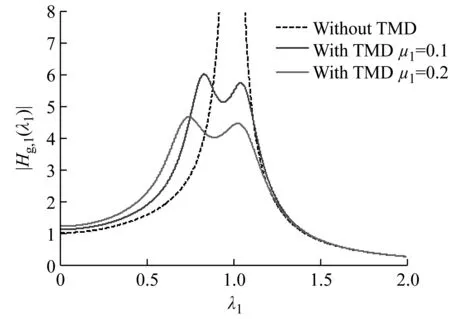
(a) τ1=1,ζg=0.80
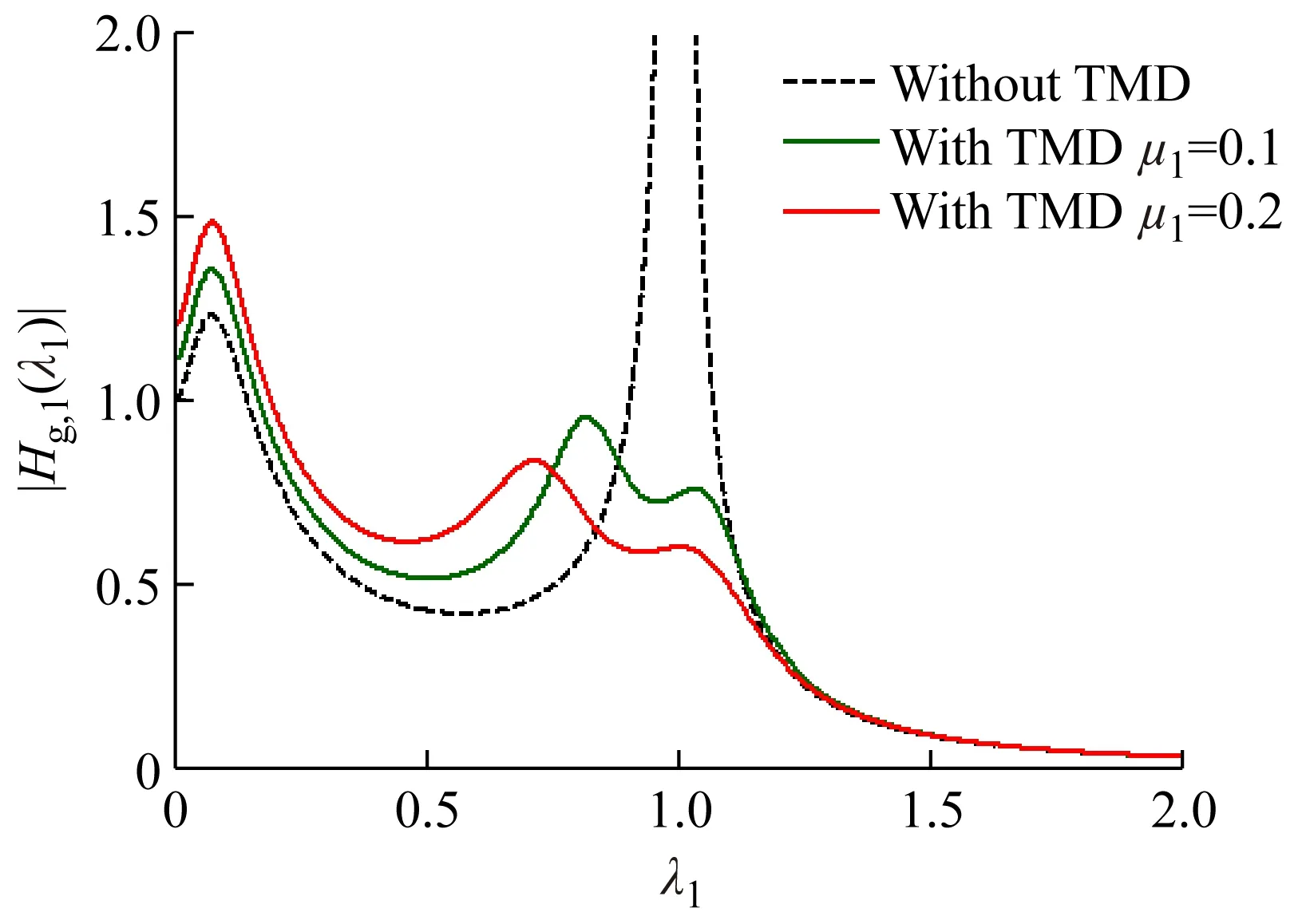
(b) τ1=10,ζg=0.80图5 主结构相对于基岩的位移动力放大系数Fig.5 Analysis results of the displacement dynamic amplification factor of structure to bedrock
然而,当τ1较大时(如τ1=10),无控状态下的Hg,1(iλ1)曲线存在两个较为明显的峰值。第一个峰值出现在场地特征频率附近,主要是由于地震加速度功率谱在该处的值较大,这一个峰值与场地因素息息相关,可将其定义为场地共振峰值。第二个峰值出现在结构自振频率附近,主要由结构参数决定,因此可将其定义为结构共振峰值。由5(b)可知,TMD虽然能有效控制结构共振峰值,却会放大结构的场地共振峰值,并且TMD质量比越大,场地共振峰值放大效应越明显。一般情况下,方法三会忽略场地共振峰值对TMD等效附加阻尼比的影响,因此会夸大TMD提供给结构的等效附加阻尼比。而本文推导的TMD等效附加阻尼比公式考虑了结构场地共振峰值的影响,理论上来说,更贴近工程实际。
5 工程算例
以某景观塔作为工程算例,来展示TMD等效附加阻尼比的求解流程。景观塔共32层,总高度168 m,采用筒体结构形式,筒体直径12 m,高宽比约为14。景观塔顶部观光层根据建筑功能和建筑体型采用钢框架结构,通过钢支撑和钢梁与核心筒连接,景观塔结构模型如图6所示。结构各阶模态阻尼比均取0.02。将结构28层的258 t消防水箱作为TMD的附加质量,用于控制结构第1阶模态响应。
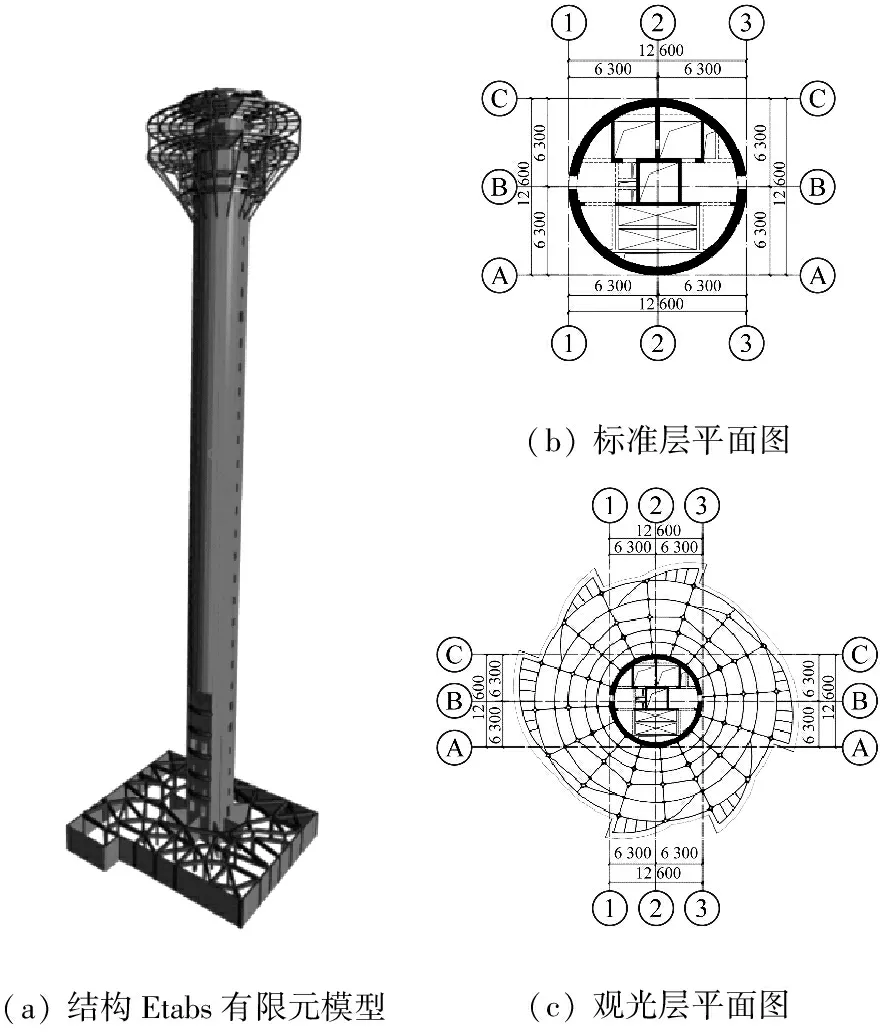
图6 肇庆景观塔结构模型Fig.6 Structural model of the view tower
为了对本文所推导的TMD等效附加阻尼比理论公式进行时程验证,选择如图7(a)~(c)所示的三组经典地震记录(1940 El Centro, 1994 Northridge以及1995 Kobe)作为地震输入,将地震记录幅值调整为0.7 m/s2,Spencer等[21]通过数值拟合得到三组地震记录的场地特征频率以及特征阻尼比分别为17 rad/s和0.3,由此可将三组地震记录功率谱与Kanai-Tajimi功率谱进行对比,结果如图7(d)所示,可以看出Kanai-Tajimi功率谱会夸大地震动的低频能量,但由于本文选择的三组地震记录低频能量较低,且能量大多集中于频段[1, 100]Hz内,在此频段内,Kanai-Tajimi功率谱与三组地震记录的功率谱是较为吻合的。
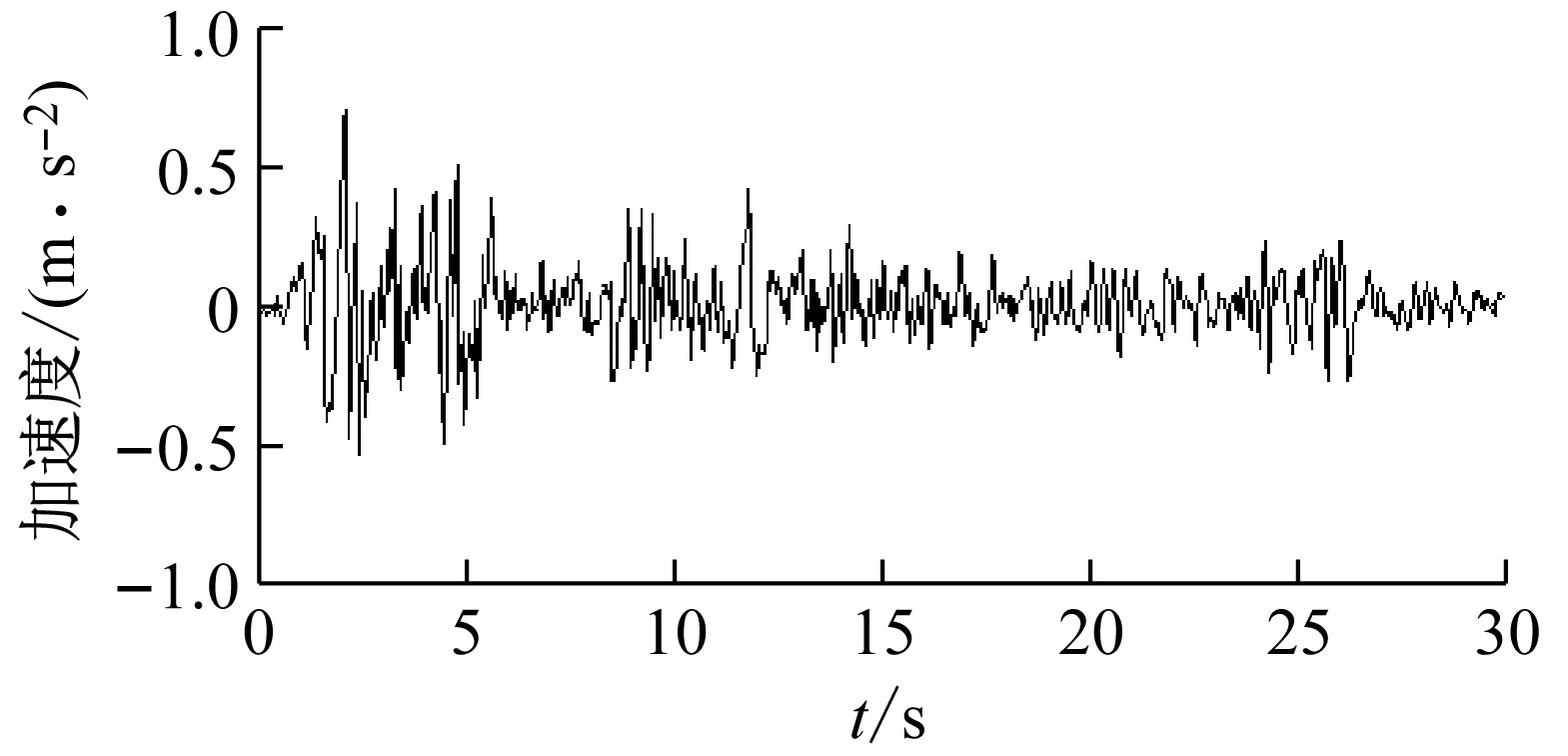
(a) El Centro
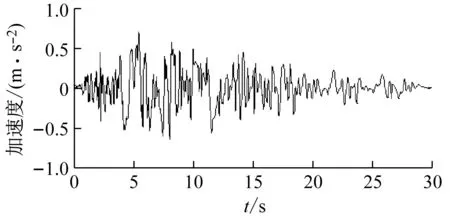
(b) Northridge
(c) Kobe
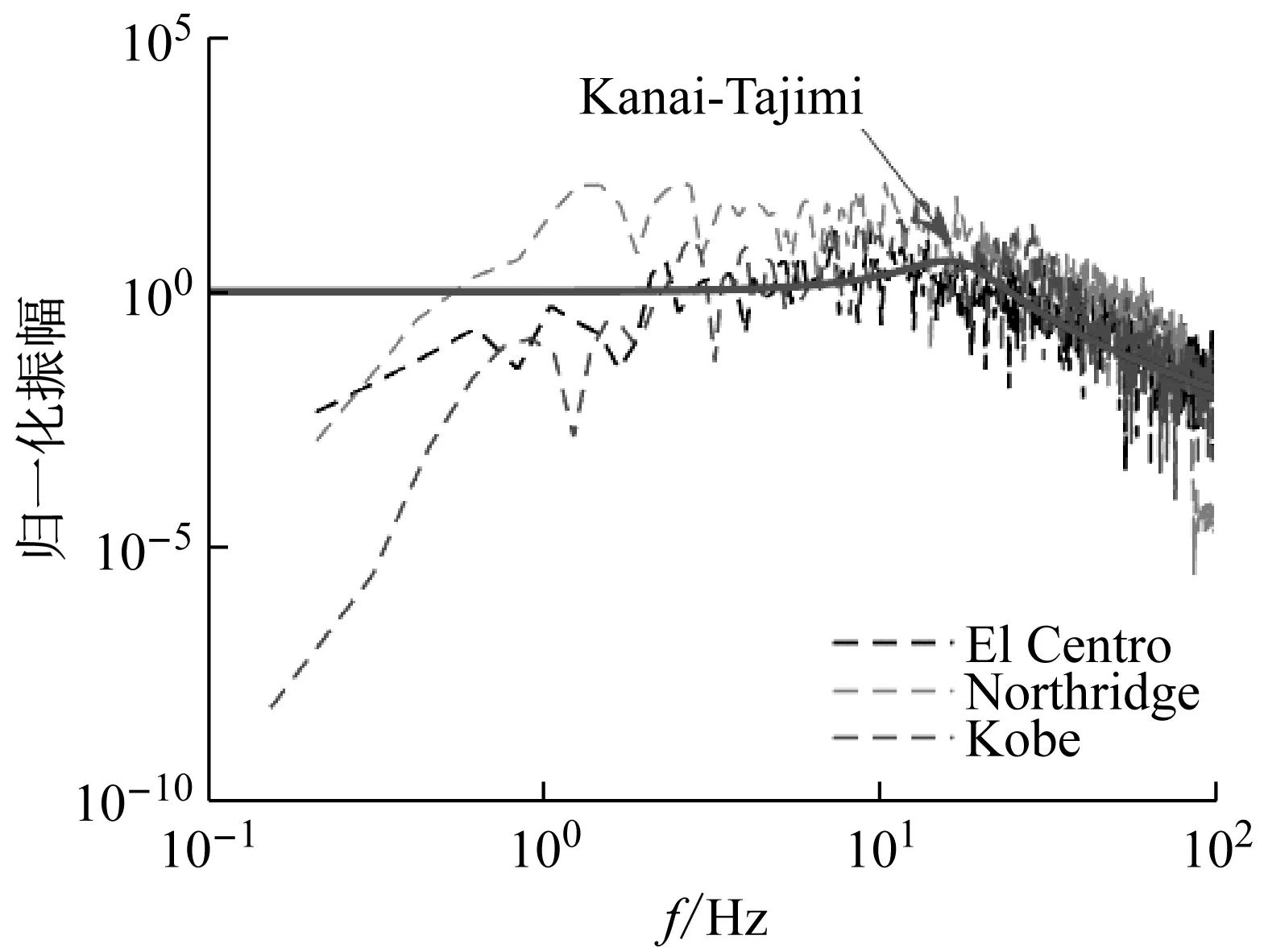
(d) 功率谱对比图7 地震记录Fig.7 Earthquake records
首先,对结构进行模态分析,表3为结构前10阶模态参数,可以看出,结构前10阶模态累计质量参与系数已经达到99.52%,因此本文重点介绍TMD对于结构前10阶模态的等效附加阻尼比。根据结构模态分析结果,采用Den Hartog公式计算TMD频率比与阻尼比。表4为TMD相对于结构前10阶模态的参数,从表4可以看出:
(1) 方法一得到的TMD提供给结构第1阶模态的附加阻尼比远大于其他高阶模态,这是因为设置TMD的主要用途是控制结构的第1阶模态响应,且TMD参数也是根据结构第1阶模态确定的;
(2) 方法一得到的TMD提供给结构高阶模态的等效附加阻尼比可能小于零,也就是说,TMD可能会放大结构的高阶模态响应;
(3) 由于方法二与方法三是基于单自由度主结构推导而来,无法计算TMD提供给结构高阶模态的等效附加阻尼比,因此方法二与方法三从理论上来说是不完备的。而本文推导的等效附加阻尼比理论公式不仅能计算TMD提供给结构高阶模态的等效附加阻尼比,还能通过结构模态坐标值考虑TMD布置位置对其等效附加阻尼比的影响,因此本文推导的等效附加阻尼比理论公式更完备。
(4) 方法二与方法三计算的TMD提供给结构第1阶模态的等效附加阻尼比均大于方法一。这是因为方法二是基于外荷载激励形式推导而来,而方法三无法考虑地震动特性对TMD等效附加阻尼比的影响,因此这两种方法的计算结果会偏大。本文推导的TMD等效附加阻尼比理论公式考虑了地震动特性引起的结构场地共振峰值的影响,因此计算结果更贴近工程实际。

表3 结构前10阶模态参数

表4 TMD相对于结构前10阶模态的参数
对结构进行时程响应分析,来验证TMD等效附加阻尼比的正确性。需要指出的是,本文时程分析均基于Etabs有限元模型展开,且在时程分析过程中,方法二与方法三仅考虑了TMD对结构第1阶模态阻尼比的影响。图8表示地震作用下结构加载与自由振动两阶段的顶层位移响应时程,从图中可以看出,使用本文推导的TMD等效附加阻尼比能从结构位移响应角度更准确地评估TMD减震性能。由此可知,使用等效附加阻尼比指标评估TMD对结构位移响应的控制效果是可行的。
为了对比三种方法的计算精度,以在景观塔有限元模型中添加TMD的时程分析结果为标准,对结构顶层位移响应进行如表5所示的误差分析。表中,结构位移响应均方差只考虑其加载阶段的响应。由表5可知,El Centro地震作用下,方法二和方法三计算结果误差较大,特别是方法三所得结构顶层位移响应峰值误差达到了21.12%,所以方法二和方法三会夸大TMD提供给结构的等效附加阻尼比,计算精度不满足工程应用需求。Kobe地震作用下,相对于结构位移响应峰值,方法一所得结构位移响应均方差误差更大。考虑到方法一所得结构顶层位移响应峰值与均方差的误差平均值均小于1%,可认为使用本文推导的TMD等效附加阻尼比理论公式能从结构位移响应峰值与均方差角度更准确地评估TMD减震性能。结合图9所示的结构各楼层位移响应峰值与均方差可知,使用本文推导的TMD等效附加阻尼比计算的各楼层位移响应与TMD控制下各楼层位移响应基本一致,再次验证了使用等效附加阻尼比指标来评估TMD减震性能的合理性与有效性。

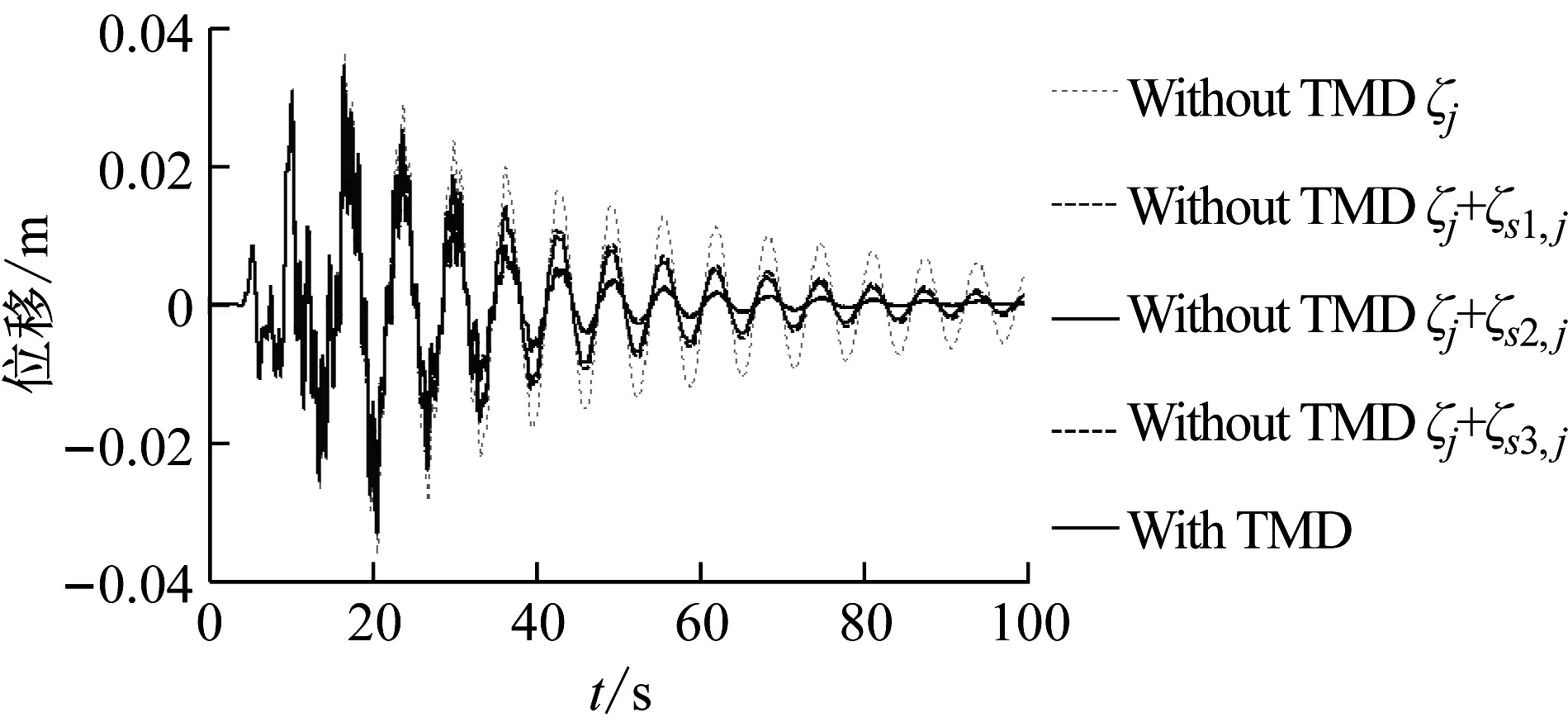
(c) Kobe图8 结构顶层位移响应时程Fig.8 Time history of structural top floor displacement responses


(a) El Centro
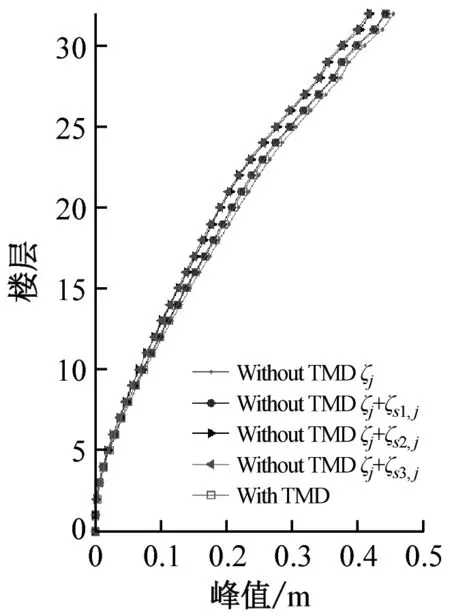
(b) Northridge

(c) Kobe图9 结构楼层位移响应峰值与均方差Fig.9 Peak and MSE value of displacement responses of structure

表5 结构顶层位移响应误差分析
6 结 论
(1) 本文推导了随机地震作用下TMD提供给结构任意阶模态的等效附加阻尼比理论公式。
(2) 参数分析结果表明,TMD等效附加阻尼比与结构场地因素紧密相关。结构与场地特征频率比小于等于1时,场地特征阻尼比越小,TMD等效附加阻尼比越大。然而,当结构与场地特征频率比大于1时,随着特征阻尼比的增大,TMD等效附加阻尼比却会变小。
(3) 算例分析结果表明,使用TMD等效附加阻尼比指标来评估其减震性能是可行的,且本文推导的TMD等效附加阻尼比公式考虑了结构场地因素的影响,能从结构地震位移响应角度更准确地评估TMD减震性能。
(4) TMD虽然能有效控制结构共振峰值,却会放大结构的场地共振峰值,并且TMD质量比越大,场地共振峰值放大效应越明显。

