侵爆作用下混凝土靶破坏效应试验与数值模拟

孙善政， 卢 浩， 李 杰， 熊自明， 邱艳宇， 王德荣

(陆军工程大学 爆炸冲击防灾减灾国家重点实验室， 南京 210007)

混凝土结构在现代防护结构中被广泛运用，其抗武器侵彻爆炸作用一直是防护领域的研究重点，也积累了大量的研究成果[1-2]。但近几十年来，混凝土材料受侵彻和爆炸作用下的毁伤效应大多是分开研究的。Forrestal等[3-5]结合试验数据和空腔膨胀理论得到了侵彻深度的半经验公式，同时，基于国内外研究，Li等[6]提出了对混凝土的侵彻进行了综述研究，解释并对比了一系列侵彻深度的计算公式。国内外学者对混凝土介质内爆炸的爆坑形态、损伤机理也进行了大量的研究。李健钰[7]在混凝土靶体中预留炮孔，研究了混凝土强度和埋深对爆炸坑形态的影响。Wang等[8]采用SPH方法对混凝土靶预留孔内的爆炸进行了分析，描述了不可逆变形区域内的破坏过程。Duan等[9]通过混凝土预留炮孔的爆炸试验，考虑了柱形装药长径比的影响，得到了临界贯穿深度的计算公式。穆朝民等[10-11]对混凝土中变埋深爆炸应力及质点加速度的变化规律进行了试验研究，给出了预估公式。刘彦等[12-14]对不同厚度壳体的带壳装药爆炸毁伤混凝土进行了试验及数值模拟研究，讨论了壳体厚度对毁伤效果的影响规律及装药埋深对带壳装药毁伤效果的影响规律。

但是，目前的介质内爆炸研究大多通过预留炮孔或者钻孔的形式装药，没有考虑侵彻对靶体造成的初始损伤，这种简化对目标受到战斗部侵彻爆炸作用时的毁伤评估是不利的。虽然也有一些关于侵彻爆炸数值模拟的研究[15-16],但由于缺少试验的对比，数值模拟结果只能给出规律性的对比，定量结果的准确性难以证实。

因此，本课题组进行了12组混凝土靶体受侵彻爆炸毁伤的模型试验。本文使用LS-DYNA软件，在模型试验的基础上对混凝土靶体侵爆作用下带壳装药毁伤效应进行数值模拟研究，针对战斗部侵爆混凝土靶体的问题，建立三种不同工况的二维有限元计算模型：① 与试验情况相同的侵彻后裸装药爆炸计算模型；② 以侵彻深度为装药埋深的预留孔裸装药爆炸计算模型；③ 不同厚度的侵彻后带壳装药爆炸计算模型。通过对比侵爆与预留孔爆炸分析侵彻初始损伤对爆炸效应的影响；通过对比裸装药和不同厚度带壳装药爆炸分析药壳厚度对爆炸效应的影响。

1 试验情况

试验中弹体材料为30CrMnSiNi2A钢, 弹头直径20 mm, 长径比为5∶1,弹头曲率半径(CRH)为2.5，弹身采用圆台形设计，弹尾直径为14 mm。弹质量约为168 g。靶体为直径800 mm，厚度500 mm的圆柱形靶体，其中7块为C30强度混凝土，5块为C40强度混凝土。装药为直径20 mm，厚度20 mm的黑索金环形药柱，单块药柱7.85 g，通过增减药柱个数调整装药量。试验中侵彻与爆炸分成两部分进行，侵彻结束后取出弹体并在侵彻隧道区底部装药起爆。试验过程中利用三维扫描仪获得了侵彻弹坑及爆炸弹坑的点云数据。试验中主要数据如表1所示，第三组试验中用水泥砂浆填充了侵彻弹坑和隧道区，混凝土靶体完全穿透，因此该组数据未显示。

表1 试验结果

图1分别显示了3号混凝土靶体的侵彻结果和5号靶体侵爆结果的成坑状态。

2 数值模拟方法

2.1 模型建立及计算方法

圆柱混凝土靶体受侵彻爆炸作用可以简化为轴对称1/2平面模型，靶体、弹体及装药药壳采用SHELL轴对称算法单元，空气及炸药采用ALE2D轴对称算法单元，空气边缘设置无反射边界。所有单元的网格均为1 mm的正方形网格。

为使数值模拟过程与试验一致，数值模拟计算中首先进行侵彻计算，侵彻计算结束后。输出侵彻后靶体的单元节点信息，同时输出单元应力应变值，通过自编程序整合为*INITIAL_STRESS_SHELL关键字的规定格式。得到能准确表达侵彻后受损靶体的模型作为爆炸初始条件。具体模型形式如图2所示。

(a) 3号靶体侵彻结果

(b) 5号靶体爆炸结果图1 模型试验现场结果图Fig.1 The results of penetration and explosive test

(a) 侵彻计算模型

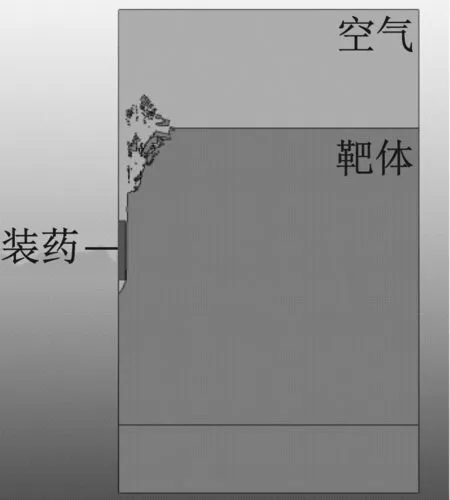
(b) 裸装药爆炸计算模型

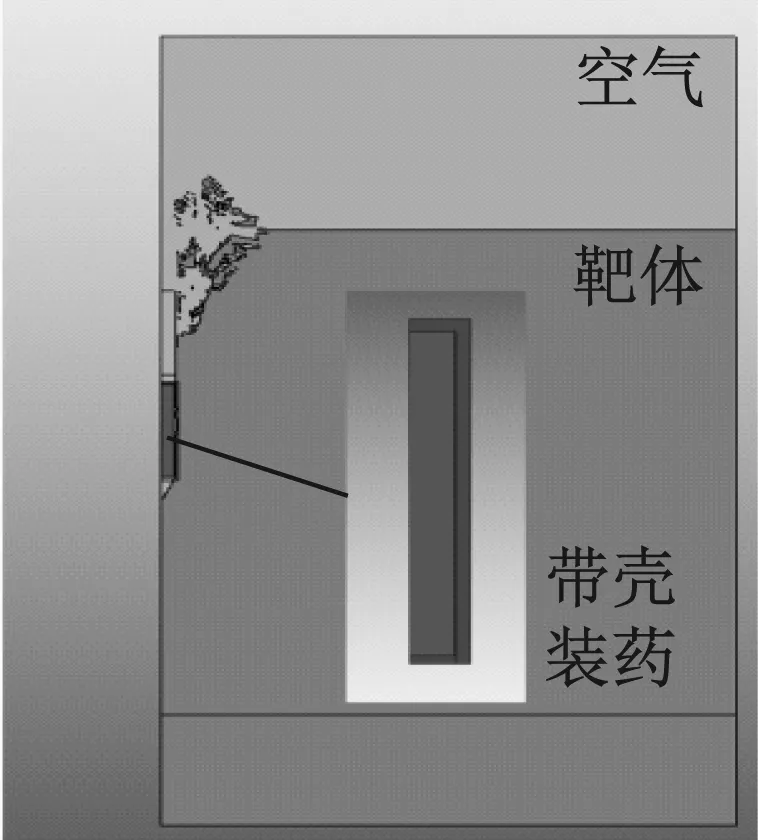
(c) 带壳装药计算模型

(d) 预留孔计算模型图2 数值模拟计算模型Fig.2 The model of numerical simulation

共进行12组侵彻及48组爆炸数值模拟，每种侵彻速度进行侵彻后裸装药爆炸(与试验情况一值)，预留孔裸装药爆炸及壳体厚度分别为1 mm、2 mm、3 mm的侵彻后带壳装药爆炸。靶体编号及侵彻速度设置与表1中一致。装药TNT当量均为39.25 g。

2.2 混凝土靶体模型材料

混凝土使用RHT本构模型，考虑了材料的应变率效应和压损损伤软化的特点，同时考虑偏应力张量第三不变量对破坏面形状的影响，用弹性极限面、失效面及残余强度面作为3个控制破坏面描述混凝土材料的初始屈服强度、失效强度和残余强度。可以很好的模拟混凝土材料在侵彻爆炸荷载条件下的损伤演化情况[17]。表2给出了RHT本构模型的主要参数。混凝土强度根据试验情况分别为30 MPa和40 MPa，尺寸与试验条件一致。

表2 RHT本构模型主要参数

2.3 炸药及空气建模

炸药建模采用MAT_HIGH_EXPLOSIVE_BURN模型，EOS_JWL状态方程。JWL状态方程的表述形式如式(1)所示，试验用炸药实测密度为1 750 kg/m3，爆速为8 300 m/s，其余参数参照文献[18]设置(如表3)。

(1)

式中：P为爆轰产物压力；V为相对体积；E0为初始内能密度；A、B、R1、R2、ω为拟合参数。

表3 炸药材料及状态方程主要参数

空气建模采用MAT_NULL模型，EOS_GRUNEISEN状态方程。参数选取参照文献。炸药尺寸与试验条件一致，空气尺寸根据爆轰产物可能到达的区域确定。

2.4 弹体及药壳建模

侵彻过程中弹体建模采用弹塑性本构模型，尺寸与试验条件一致。爆炸模拟时，壳体采用Johnson-Cook本构模型，主要参数如表4所示。

表4 炸药材料及状态方程主要参数

3 数值模拟方法的验证

通过12组侵彻和装药量39.25 g的8组爆炸试验结果对侵彻后裸装药爆炸数值模拟结果进行了验证。

图3显示了数值模拟侵彻深度对比，图4、图5分别显示了终态弹坑深度、弹坑半径对比。此外，限于篇幅，图6基于试验结果的3D云图，比较了两组工况试验与数值模拟中的侵彻弹坑和终态弹坑形态。

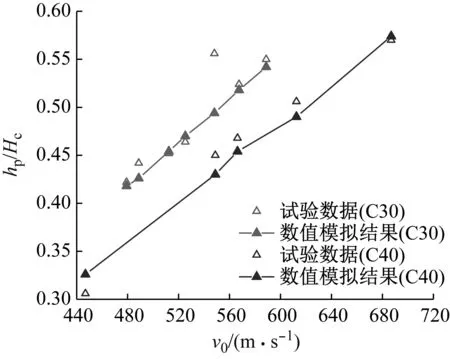
图3 侵彻深度对比Fig.3 Comparison of penetration depth between test and simulation results

通过对图3～图6进行分析，可以发现数值模拟结果较试验结果偏小，这与试验中在装药附近填塞炮泥有关。但数值模拟结果呈现了与试验相同的规律，且两者侵彻深度误差在10%以内，终态爆坑尺寸误差稳定在11%左右。说明了数值模拟方法及材料参数设置比较合理，得到的侵爆终态爆坑的结果与试验结果相比较为稳定。通过数值模拟方法研究侵彻初始损伤及装药药壳厚度对爆炸结果的影响是合理的。

图4 侵彻后裸装药爆炸终态弹坑深度对比Fig.4 Comparison of final explosive crater depth between test and simulation results

图5 侵彻后裸装药爆炸终态弹坑半径对比Fig.5 Comparison of final explosive crater radius between test and simulation result

试验编号5号靶体侵彻弹坑5号靶体终态弹坑9号靶体侵彻弹坑9号靶体终态弹坑试验扫描云图模拟损伤云图

4 讨论与分析

4.1 量纲分析

影响混凝土靶体受侵彻后带壳装药爆炸问题的因素很多。从理论上建立完备的数学和力学模型较为困难。因此建立合适的物理模型，找出影响毁伤效果的主要参量，并通过试验和数值模拟结果找到主要参量与毁伤效应量之间的关系成为研究该问题的有效手段。本文主要考虑：① 两个毁伤效应量，包括终态爆坑深度he及半径Re；② 炸药几何与材料参数，包括带壳装药的长度Le和直径de，壳体厚度δ，装药质量me，爆热Qv，爆速vD；③ 混凝土几何与材料参数，包括靶体厚度Hc，密度ρc，抗压强度fc；④ 侵彻弹体参数，包括弹头形状系数N，弹体质量M，侵彻速度v0，弹体直径d。

即毁伤效应量的表达式可以写为

Re(he)=f(Le,de,δ,me,Qv,vD,Hc,ρc,fc,N,M,v0,d)

(2)

基本量选为fc，d，vD，根据π定理对式(2)进行无量纲化，得到10个π项。

(3)

根据参数的物理意义对π项进行调整，将第8项弹头系数N写入第10项，第4项与第6项并不相互独立，保存第6项。则可以将终态弹坑深度及半径的表达式可以写为

(4)

式中：Ie为无量纲爆炸系数，表征炸药与靶体的相互作用；Ip为无量纲冲击系数，表征侵彻弹体与靶体的相互作用，其表达式为

(5)

由于本文涉及的装药长径比一致，且混凝土材料密度差别不大，后续分析中忽略这两个影响因素。则可以将终态弹坑深度及半径的表达式为

(6)

下面结合数值模拟结果，分析各因素对终态爆坑半径及深度的影响。

4.2 侵爆与预留炮孔爆炸的对比分析

侵彻初始损伤主要包括侵彻造成的开坑及侵彻过程中弹体对周围介质的损伤，其中侵彻开坑会增大泄爆孔，使爆炸压力倾向于通过侵彻隧道区及侵彻坑向外泄露，而不是作用于混凝土介质中，从而削弱爆炸毁伤效果；而侵彻造成的介质损伤则会削弱装药周围的混凝土材料的抗爆性能，从而使爆炸毁伤效果增强。

为探究弹体低速侵彻混凝土靶体后的浅埋爆炸中，两种影响的复合情况，将预留孔爆炸及侵彻后爆炸的数值模拟结果进行对比，如图7、8、9所示。

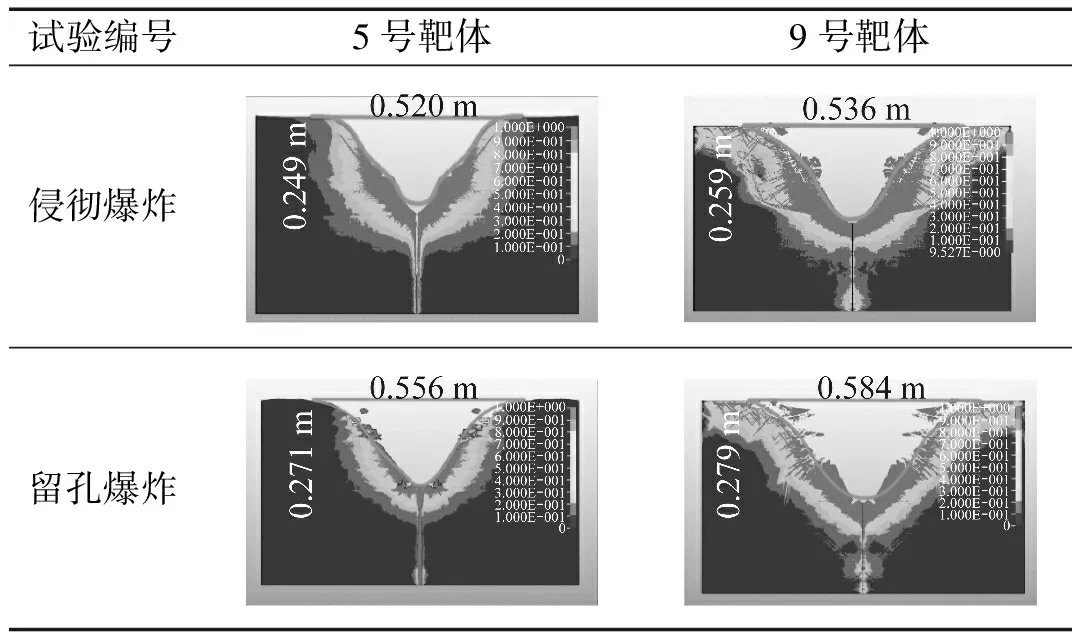
试验编号5号靶体9号靶体侵彻爆炸留孔爆炸

图8 预留孔爆炸与侵彻爆炸的终态弹坑深度对比

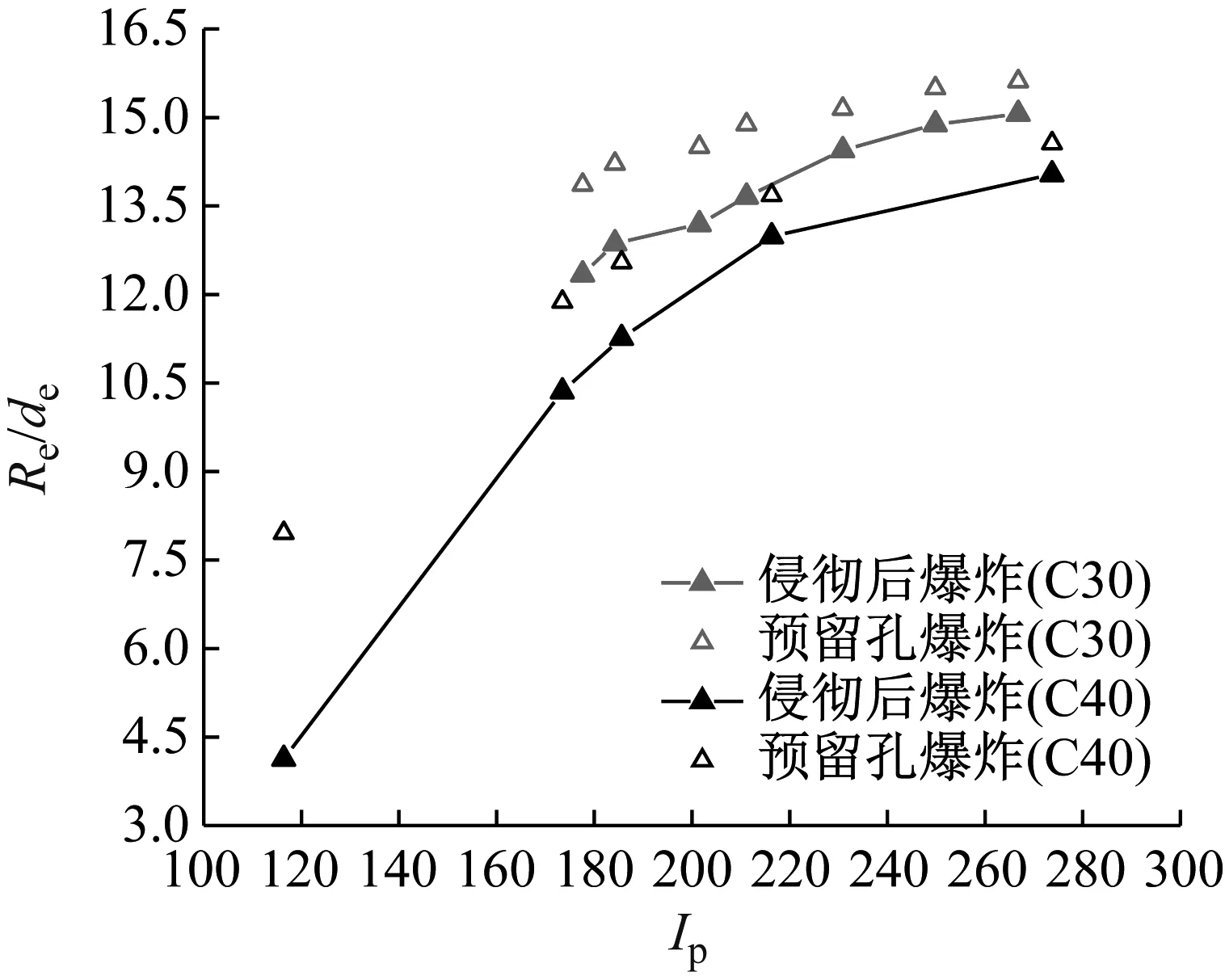
图9 预留孔爆炸与侵彻爆炸的终态弹坑半径对比

由图7～图9可知，预留孔爆炸与侵彻后爆炸的终态弹坑形状较为相近，但爆坑尺寸不同，总体来说，侵彻后爆炸的爆坑尺寸较小，爆坑半径及深度均小于预留孔爆炸。说明弹体低速侵彻混凝土后浅埋爆炸时，侵彻弹坑引起的孔口泄压影响起主要作用，侵彻初始损伤会削弱爆炸作用的影响。同时由图8、图9可知，这种影响是随着冲击系数的增加而减弱的，侵彻后爆炸坑的尺寸与预留孔爆炸坑尺寸随着冲击系数的增大愈加接近。这是由于侵彻弹坑的深度不会随着侵彻速度的增大一直增大，因此侵彻深度的增加使装药位置远离侵彻坑底部，侵彻弹坑造成的孔口泄压影响减小，侵彻造成的介质损伤影响增大。

图8、图9中均给出了两种强度混凝土的结果，其中C30混凝土Ie值为12 521；C40混凝土Ie值为9 391。可以发现，终态弹坑半径随Ie值的增大而增大，与IP值无关。这一规律区别于终态弹坑深度，在IP值较小时，不同的Ie值造成的终态弹坑深度区别不大，但随着IP值的增大，较大的Ie值造成的弹坑深度明显大于Ie值较小时。这是由于当IP值较小时，装药埋深较浅，更多的装药也无法作用于装药底部的混凝土介质中。

4.3 不同壳体厚度对爆炸毁伤效应的影响分析

为探究不同壳体厚度对侵彻后爆炸效果的影响，将不同壳体厚度的侵彻后爆炸结果进行对比。图10给出了不同弹壳厚度下的5号、9号靶体的终态弹坑形态。图11、图12给出了12组不同工况下终态弹坑无量纲深度及半径的对比。

试验编号5号靶体9号靶体壳体厚度(0 mm)壳体厚度(1 mm)壳体厚度(2 mm)壳体厚度(3 mm)

图11 不同弹壳厚度的终态弹坑深度对比Fig.11 Comparison of final explosive crater depth between different shell thickness

通过图10可以看出，总体来说，药壳的存在使爆坑形状变得更加瘦长。通过图11、图12可以看出，当药壳为1 mm时，爆坑半径基本无变化，部分工况爆坑半径比裸装药情况大，爆坑深度略微增大；当药壳厚度继续增大时，爆坑半径加速减小，爆坑深度基本保持不变。这是由于：① 壳体厚度较小时，壳体破坏消耗的能量较少，且壳体使得爆轰产物产生聚集效应。此时爆坑深度略有增加，爆坑半径减小也较少，甚至略有增加。② 壳体厚度较大时，爆炸产生的能量更多的消耗在破坏壳体上。因此爆坑深度不在增加，爆坑半径加速减小。

图12 不同弹壳厚度的终态弹坑半径对比Fig.12 Comparison of final explosive crater radius between different shell thickness

图13 终态弹坑体积随壳厚的变化Fig.13 Variation of final explosive crater volume with shell thicknesses

可以发现，爆坑体积随无量纲壳体厚度先增大后减小，大约在δ/de=0.025时达到最大值，达到带壳装药对混凝土靶体的最佳毁伤效果。

5 结 论

(1) 对比数值模拟结果与试验结果，验证了二维模型侵彻爆炸计算的有效性及参数设置的合理性。侵彻深度误差小于10%，终态爆坑尺寸误差小于15%。

(2) 通过量纲分析得到混凝土靶体受侵彻后带壳装药爆炸毁伤效果的主要影响因素，并总结为无量纲冲击系数、无量纲爆炸系数及无量纲壳体厚度。

(3) 对比侵彻后裸装药爆炸与预留孔爆炸结果表明：低速侵彻后的浅埋爆炸中，侵彻弹坑引起的孔口泄压影响起主要作用，侵爆终态爆坑尺寸小于预留孔爆炸；随着冲击系数的增大，孔口泄压影响减小，侵爆终态爆坑尺寸接近预留孔爆炸。

(4) 对比不同装药药壳厚度的侵彻后爆炸结果表明：较小的壳体厚度会使爆轰产物产生聚集效应，终态弹坑尺寸较裸装药相比略微增大；较大的壳体厚度会消耗更多炸药能量，抵消了爆轰的聚集效应，终态弹坑半径快速减小。综合分析，当δ/de=0.025时，带壳装药对混凝土靶体的毁伤效果最佳。

本文研究的范围为中低速侵彻后的浅埋爆炸，没有进一步分析高速侵彻后的完全埋深爆炸问题。同时，对侵彻造成的介质损伤量化方法仍需进一步研究。