基于多项式修正片条气动力的跨音速颤振分析方法及其试验验证

张婷婷， 周健斌， 窦忠谦， 章俊杰

(上海飞机设计研究院，上海 201210)

飞机的跨音速颤振特性研究是民机颤振设计的重要部分。当前，国内民机的颤振设计工作主要是通过跨音速颤振模型风洞试验来获得飞机部件的跨音速压缩性曲线[1-4]。在分析方面，由于跨音速区的气流存在激波、流动分离等问题，精确的跨音速颤振计算(尤其在高马赫数区)存在很大的难度。

近年来，随着计算流体力学技术的发展，基于欧拉方程/N-S方程以及结构动力学方程的时域颤振分析方法取得了一定进展[5-8]，但是其计算量大、耗时长。基于小扰动线性谐振荡假设的面元法，计算效率快、计算精度高，在工程颤振分析中发挥着重要作用，由于其不能考虑攻角、翼型的影响，在跨音速颤振计算时，通常需要先对气动力进行一轮修正。近年来，国内学者对面元法的气动力修正方法进行了研究探索[9-11]，但大多用于理论分析，在民机颤振设计工程中少有应用。

本文以MSC.NASTRAN软件为平台，提出一种适用于工程应用的，基于多项式的气动力修正方法，以片条内升力和力矩随攻角变化斜率为修正目标，用一组多项式方程模拟片条力矩分布，保证整个翼面的气动力大小和分布都与目标相符，进而使用修正后的气动力进行跨音速区的颤振分析。该方法适宜于工程使用，快速有效，且已在某型民机的跨音速颤振模型风洞试验中得到了应用和验证，计算结果的跨音速压缩性曲线趋势与试验一致，凹坑马赫数一致。

1 方法介绍

面元法无法考虑翼面厚度、非线性影响等因素，在跨音速区计算的气动力与实际有一定偏差。并且由于非定常气动力计算机理复杂，影响因素众多，计算精度通常难以保证，直接修正非定常气动力数据存在较大难度。使用计算流体力学(computational fluid dynamics, CFD)可以求解非线性的流场，得到准确的定常气动力数据，对面元法的定常气动力部分进行修正，得到气动力修正系数矩阵Wkk，然后将Wkk应用于所有频率段中的非定常气动力修正，使用修正后的非定常气动力进行颤振计算，可有效提高跨音速区颤振分析的准确性。

MSC.NASTRAN软件采用偶极子格网法(doublet-lattice method,DLM)计算气动力，本文使用CFD计算的定常气动力去修正DLM计算的定常气动力，得到Wkk，然后将Wkk应用于所有频率段中的非定常气动力修正，使用修正后的非定常气动力进行颤振计算。修正气动力的跨音速颤振计算流程图，如图1所示。

图1 气动力修正的跨音速颤振计算流程图Fig.1 Flow chart of transonic flutter calculation based on aerodynamic force modification

1.1 气动力修正原则

为保证修正后的气动力与目标尽可能相似，需要确保力的大小和分布均与目标相同，即力和力矩与目标相同。如果选择以网格为单位进行气动力修正，保证各网格气动力与目标相同，由于DLM各网格的压心位置是固定的(1/4弦长处)，而CFD各网格的压心位置都不同，网格的力矩无法满足目标要求。因此，将翼面沿展向划分为若干片条，以片条为单位，通过协调各网格的气动力大小，来保证整个片条的力和力矩与目标相同。

由于CFD计算的力和力矩的零升攻角不同，对应于DLM的某一给定攻角，CFD的力和力矩处于不同的攻角状态,无法以某一攻角状态的力和力矩为目标来做修正。而在小攻角范围内，升力和力矩随攻角变化近似为线性的，可以选取该线性变化的斜率作为修正目标。同时，为确保力和力矩的斜率大于0，修正系数也必须大于0。

1.2 气动力修正对象

DLM的气动力和力矩随攻角的变化曲线为过原点的直线，因此，1°攻角时的气动力和力矩即为升力和力矩随攻角变化的斜率。同时，DLM网格的压心位置是确定的，所以力矩分布是由气动力的分布决定的。因此，选取1°攻角状态的各网格气动力作为修正对象。应用MSC.NASTRAN软件的静气动弹性分析模块，计算给定马赫数下1°攻角状态翼面上各网格的气动力L0。

1.3 气动力修正目标

建立CFD模型，计算翼面在给定马赫数和攻角状态(选取小角度范围-5°～5°)下的定常气动力，得到各片条站位下的压力系数分布曲线，如图2、图3所示。

图2 CFD计算模型示意图Fig.2 The CFD model

图3 单片条内压力曲线分布示意图Fig.3 Pressure curve distribution in a single strip

对每个气动网格区域内的CP进行积分，得到对应于每个气动网格的升力系数CLi、压心位置Xi

(1)

(2)

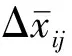
再计算出各片条的升力L和对前缘点的力矩M

L=∑(CLi·Si)

(3)

(4)

M=L·(X-X0)

(5)

式中:Si为第i个计算网格的面积;X为片条压心坐标;Xi为第i个网格的压心坐标;X0为网格前缘点坐标。

绘制片条升力和力矩随攻角变化曲线，取小角度范围内的线性段斜率，作为气动力修正要满足的目标。

1.4 基于多项式的气动力修正方法

一个片条内弦向通常划分有多个网格，即修正系数为多个未知量，需同时满足两个等式方程和一组不等式方程，为多解问题，求解困难。

本文提出一种基于多项式的气动力修正方法，用一组多项式方程来描述片条内弦向网格的力矩分布，各片条的多项式方程根据片条力矩具体分布情况进行调整，目的是将未知量降为3个，求解后可得到一组求解区间，在区间内取值，都满足力和力矩与修正目标相同的等式方程。

为选出与目标气动力分布符合性最好的最优解，绘制出各片条内升力和力矩的分布曲线，在求解区间中调整参数，选取升力和力矩分布曲线与目标曲线趋势相同，与目标差值均方差最小的修正系数作为最优解。修正后的片条内弦向网格的升力斜率和力矩斜率分布示意图如图4、图5所示。

M=ax2+bx+c

(6)

(7)

(8)

式中：a、b、c为多项式函数的常数项；x代表片条内弦向网格位置。

图4 片条内弦向网格升力斜率分布示意图Fig.4 Lift slope distribution of tangential grid

气动力修正系数矩阵Wkk的目的是使偶极子格网法计算的升力和力矩匹配CFD计算的升力和力矩，其元素Wij为翼面各网格的气动力修正系数。

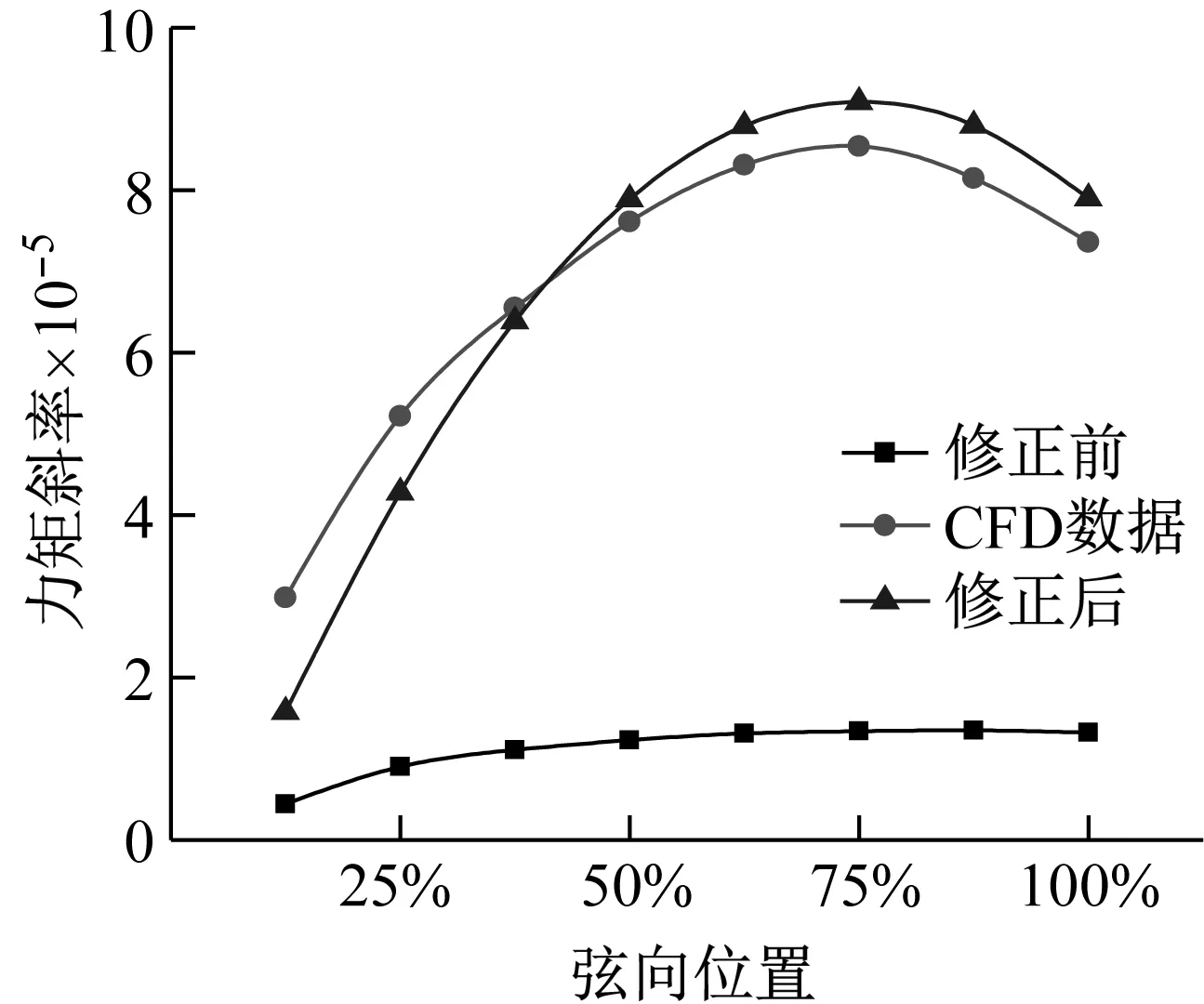
图5 力片条内弦向网格力矩斜率分布示意图Fig.5 Moment slope distribution of tangential grid

(9)

式中，Lij为确定各片条的a、b、c常数项后，得到的片条内各网格修正后的升力。

1.5 气动力修正后的颤振分析

气动弹性一般运动方程写为以下的形式

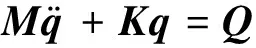
(10)

式中:q为广义坐标列阵;M为广义质量对角矩阵;K为广义刚度对角矩阵;Q为广义非定常气动力列阵。

将气动力修正系数矩阵Wkk用于非定常气动力的计算

(11)

式中:FP为网格气作用点处的模态矩阵;S为面积加权阵，对角项为各气动网格的面积;D为非定常气动力影响系数;FH为控制点的模态矩阵;k为减缩频率;t为参考长度。

使用修正后的广义非定常气动力Q，用p-k法进行颤振方程求解，得出颤振速度与颤振频率。

2 风洞试验验证

2.1 翼吊发动机机翼构型

某型民机机翼跨音速颤振风洞试验模型为翼吊发动机构型的单机翼模型，主要部件包含主翼面、小翼、吊挂和发动机。如图6所示。试验风洞截面为正方形，尺寸2.4 m×2.4 m，试验段长7 m，是引射式、半回流、暂冲型跨声速风洞，风洞可用马赫数范围为0.3～1.2。试验获得了以下马赫数的临界颤振速度：0.60、0.70、0.75、0.80、0.82、0.85。

气动网格示意图如图7所示，使用本文中的分析方法对机翼翼面的气动力进行修正，并进行了颤振分析。将跨音速区的计算结果与风洞试验结果进行对比，结果如表1和图8所示(颤振速度已经过无量纲处理)。

图6 机翼跨音速颤振模型风洞试验照片Fig.6 The wing flutter model in the wind tunnel

图7 机翼气动网格示意图Fig.7 FEM model of the wing structure

从计算结果可以看出，在高马赫数区，修正前的计算结果无法得到速度凹坑，通过气动力修正，计算结果较好地获取了跨音速区颤振特性，速度随马赫数变化趋势与试验曲线一致，且速度最低点马赫数区域与试验结果一致，当量颤振速度偏差在5%以内，计算结果绝对值总体低于试验值，偏于保守。在低马赫数区，气动力修正对颤振计算结果影响较小。

2.2 带操纵面的尾翼构型

某型民机平尾跨音速颤振风洞试验模型为带操纵面构型的单平尾模型，主要部件包括水平安定面、升降舵、以及舵面连接机构。如图9所示。在风洞试验前，应用本文中的分析方法计算出颤振速度随马赫数变化曲线，以此为基础，规划吹风试验点,试验点规划示意图如图10所示，相比传统的逐步逼近亚临界颤振点的吹风方法，车次减少了近30%，试验成本和风险都显著降低。

图9 平尾跨音速颤振模型风洞试验照片Fig.9 The horizontal tail flutter model in the wind tunnel

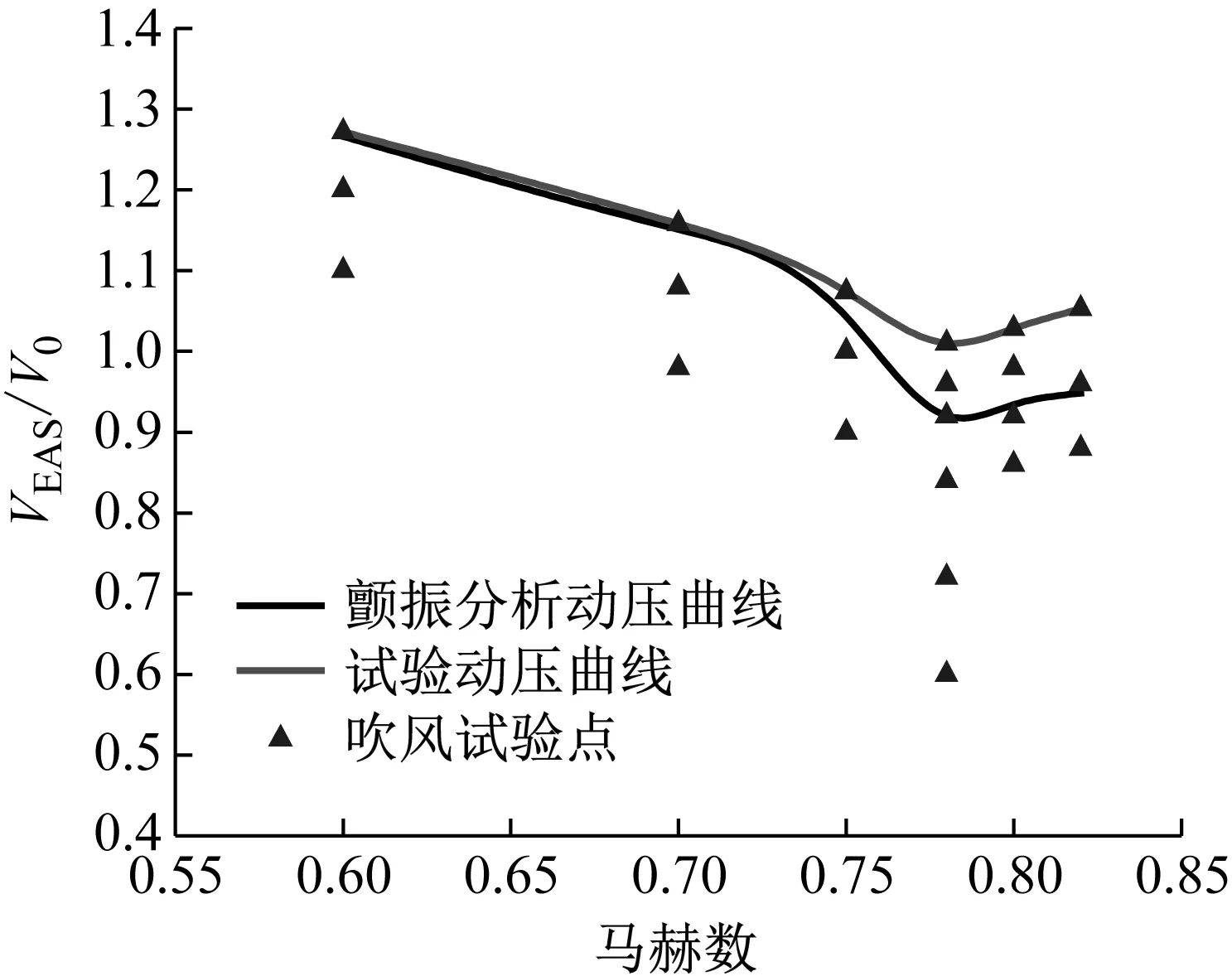
图10 试验点规划示意图Fig.10 Test site planning

试验获得了以下马赫数的临界颤振速度：0.60、0.70、0.75、0.78、0.80、0.82。颤振计算结果如表2所示(其中，颤振速度已经过无量纲处理)。

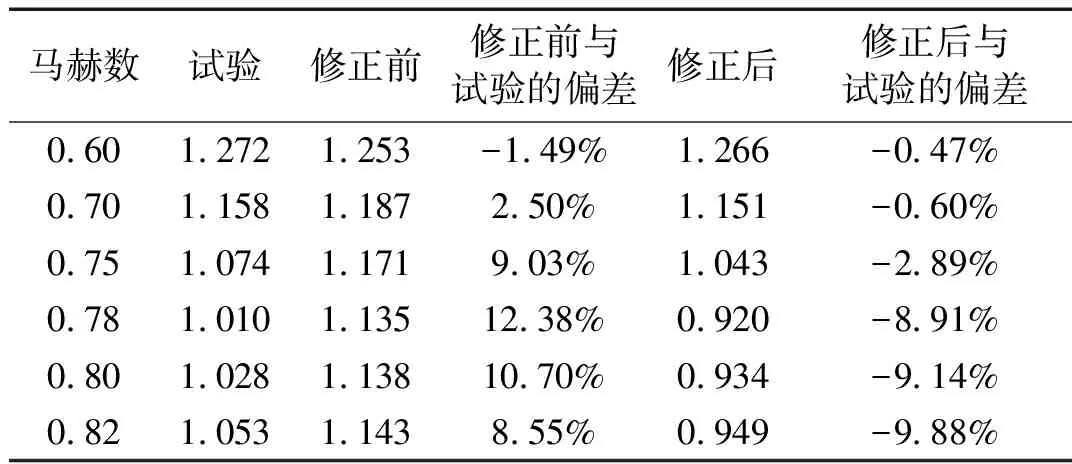
表2 平尾模型颤振计算结果

从计算结果可以看出，在跨音速区，颤振速度随马赫数变化趋势与试验一致，速度凹坑点马赫数区域与试验一致，马赫数在(0.60～0.75)区间内，当量颤振速度最大偏差小于3%，马赫数在(0.78～0.82)区间内，当量颤振速度最大偏差在10%以内，计算结果绝对值总体低于试验值，偏于保守。

3 结 论

本文提出了一种适用于工程的，基于多项式的气动力修正方法，准确模拟了翼面的气动力分布，使用修正后的气动力进行颤振计算，提高了跨音速区的颤振计算精度。跨音速颤振模型风洞试验表明：

(1) 该方法对翼吊发动机构型的机翼颤振型、带操纵面的尾翼颤振型都有较高的精度，且分析结果偏保守。

(2) 计算获得的跨音速压缩性曲线和试验结果相比，曲线趋势一致，凹坑位置一致。

本文主要针对大展弦比的翼面(如机翼、平尾)进行了气动力修正，发动机、机身的气动力修正方法及其对颤振分析结果的影响有待进一步研究。