双临空面条件下隧道爆破近区振动波形构造与应用

龚 敏， 曹贞洋， 石发才， 吴昊骏， 吴晓东, 周世均

(1.北京科技大学 土木与资源工程学院，北京 100083; 2.重庆中环建设有限公司，重庆 401120)

爆破振动是工程爆破灾害控制的首要问题，振动预测是爆破设计施工的重要依据[1-2]。在当前普遍强调低振速、高安全爆破形势下，根据预测合成振速进行爆破参数计算具有重要的理论与工程应用价值。

近年来基于单孔波形叠加的安德森法成为微差振动合成研究的主要方法[3-5]。现场单孔爆破振动波形隐含了药量和传播介质的信息，但计算数据是基于现场单自由面爆破获取[6]，只能计算时间很短的掏槽初期振动合成，不适用于占主要爆破过程的第二自由面形成后时段，现有研究仍未能获取多临空面下的单孔波形；其次大多数研究[7-8]将隧道各微差炮孔视作同一位置，仅适用于爆源距保护物较远位置情况，对不能忽略炮孔位置影响的爆源近区振动合成(如小净距隧道爆破)精度较差。文献[9-10]获取单孔单自由面爆破后爆源近区不同测点振动数据，基于主频修正得基础波形，并用比例系数构造其它位置单孔波形，该方法较便捷，但未考虑振动能量实际分布于不同的优势频带[11]，计算波形与实测波形在峰值、频率上存在误差。

为解决双临空面下爆源近区不同炮孔单孔振动波形重构与微差振动合成问题，以深圳莲塘隧道为研究背景，在非电-数码雷管混合起爆网络下，通过现场试验获取正常施工时有限单孔振动数据，采用小波包变换将单孔波形分解为各优势频带多个子波；拟合各频带子波最大振速峰值与炮孔药量、爆心距的相关函数，获得不同频带的子波后叠加构造所有位置炮孔单孔波形，利用计算程序得到保护物不同延时振动叠加波形，据此调整爆破参数。这一方法扩展了振动叠加法的适用范围，提高了预测准确性，对实现隧道精准控制爆破具有重要意义。

1 工程背景及爆破方案

莲塘隧道所属深圳东部过境高速公路是《粤港合作框架协议》编列的重大基础建设项目，隧道SLK1+838～880为小净距段，中夹岩仅8～0.5 m宽，为世界最小净距隧道之一。

为确保后行洞爆破时中夹岩安全，同时形成双临空的爆破条件，作者现场设计了从岩柱远端创造临空面和逐步逼近岩柱的三步开挖方案(图1)。其中远离中夹岩第I部分首先开挖，第II部开挖因与保留岩柱直接相联，是小净距段爆破振动控制关键区段。本文以II区为研究对象，在如图2所示试验设计下，II区最大宽度仅3 m，所有炮孔爆破前均在双临空面条件下。

图1 小净距开挖方案图(cm)Fig.1 Excavation plan for small spacing (cm)

从减少爆破振动并兼顾爆破成本考虑，II区采用非电雷管-电子雷管混合起爆网络：距保留岩柱较近部位设计电子雷管逐孔微差爆破以减少爆破振动；其余部位视与岩柱距离采用非电雷管1～多孔同段起爆，图2为第II部实际爆破布孔与网络图。图中标注MS的实心孔装非电雷管，直接标注延期时间的为电子雷管起爆孔，为表达简洁，以下用MS1、MS3、960 ms、965 ms…指代该炮孔所在位置。图2中空心圆孔是防止风钻钻孔角度限制造成欠挖而设计的补偿炮孔，其装药量很小。

图2 II区实际炮孔布置与爆破网络图Fig.2 Actual blast hole layout and blasting network diagram of area II

2 主要研究方法与原理

2.1 研究方法

通过现场获取双临空面下有限个单孔振动波形，构建爆破控制关键区(即电子雷管起爆孔)任意炮孔位置、不同药量下的单孔爆破振动波形，据此进行微差振动合成和峰值振速预测，确定安全振速下最优延期时差。研究的核心是任意炮孔位置、药量下单孔波形构造，图3为单孔爆破振动波形构造步骤图。

图3 单孔波形构造步骤Fig.3 Single hole waveform construction process

根据图3步骤，按现场试验的雷管起爆顺序截取出符合要求的有限单孔波形后，分析其振动波形的频率分布情况。由于不同频率地震波在岩土中传播时幅值衰减速率并不相同[12]，采用小波包变换确定振动能量占比较大的频带为优势频带，将实测单孔波形分解为各优势频带上的子波进一步分析。非线性拟合各炮孔爆心距、药量和不同频带子波的最大振速峰值的关系式，确定不同频带上的振速衰减函数，据此构造各频带子波，进而构造同一测点处爆区不同位置炮孔爆破单孔波形。

2.2 双临空面条件下有限单孔波形的现场获取方法

获取现场双临空面下有限个单孔波形是构建任意位置炮孔单孔波形的基础，考虑到被爆区间右侧是需保护的小净距中夹岩，故爆区右侧采用电子雷管逐孔起爆；在远离中夹岩的左侧设计非电雷管跳段起爆以获取不同距离单孔爆破振动波形(见图2)。第五段、第七段和第九段的标准时间间隔近100 ms，根据经验可知单孔波形基本在100 ms内已衰减为0。故设计第五段和第七段为单孔单响，以在测点处获取不同距离的多个单孔爆破振动波形。为此按图4在先行两车道内布设间距10 m的三个振速测点，三个测点距II区爆破断面上1 065 ms炮孔的水平距离Rxy分别为4.4 m、11.8 m和21.7 m，垂直距离Rz均为1.8 m，计算得净距离R分别为4.8 m、12.0 m和21.8 m。使用中科测控有限公司TC-4850型三向爆破测振仪进行振动数据采集。

图4 测点布置平面图Fig.4 Plan of measuring points

2.3 小波(包)变换原理简述

小波变换是一种时间窗和频率窗都可以改变的时频局部化分析方法，其基函数迅速衰减的特性与爆破振动波形的变化相契合[13]。小波变换将振动信号逐层分解为低频和高频两个部分，每一层都是对上一层低频信号的继续分解。小波包变换在小波变换的基础上对未分解的高频细节部分也进一步分解，使得相同宽度的低频频带和高频频带具有相同的分辨率[14-15]。

采样频率为f0的振动信号，其奈奎斯特频率为f0/2，若进行小波包N层分解，可得到共2N个频带，每个频带宽度为f0/2N+1。已知离散信号各频带上的能量Ei可用相应频带所有采样值的平方和表示

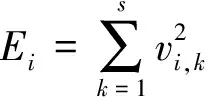
(1)

式中：vi, k为第i频带上的第k个采样值;s为信号中采样点个数。则进行小波包N层分解后不同频带能量相对于信号总能量的占比为

(2)

若将能量占比大的频带记为优势频带，对特定优势频带单支重构可得到相应频带的子波fi(t)。由于小波包变换属于线性变换，不考虑能量占比小的频带，只对多个优势频带子波进行叠加可得滤波后的波形f(t)

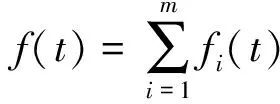
(3)

式中：i为优势频带编号;m为优势频带数量;fi(t)为优势频带子波。

2.4 单孔波形构造方法

基于上述小波包变换理论，本文提出考虑频域特征的单孔波形构造方法。将实测单孔波形小波包分解为各优势频带的子波，利用非线性拟合不同频带的子波最大峰值和药量、爆心距函数关系，得到各频带的最大振速衰减函数。

vi=kiQaiR-bi

(4)

式中：vi为优势频带的最大振速;ki、ai、bi为相应优势频带上的衰减系数。

根据式(4)的形式，同一频带上不同子波的最大振速之比可表示为

vi,1/vi,2=(Q1/Q2)ai(R1/R2)-bi

(5)

由于同一频带上的子波频率相近，药量和距离主要影响的是各时刻的振动幅值。假设不同子波在任意相同时刻的幅值之比均满足式(5)的关系，并将药量为Q0、爆心距为R0的实测单孔波形在各频带子波fi, 0(t)记作基础子波，则根据炮孔药量、距离比例变化调整基础子波幅值，构造出不同爆破参数的炮孔在各频带的子波fi, j(t)。

fi,j(t)=(Qj/Q0)ai(Rj/R0)-bifi,0(t)

(6)

式中：j为炮孔编号;Qj、Rj为各位置炮孔的药量、距离参数。

将式(6)所得各频带构造子波按照式(3)进行叠加，构造单孔波形fj(t)。

(7)

2.5 隧道爆破振动叠加合成方法

根据Anderson等的研究，可知线性叠加原理进行爆破振动波形的预测是可行的。假设各炮孔的单孔波形为fj(t)，相应延期时间记作Tj，则n个炮孔微差爆破后的振动波形可表示如下

(8)

基于上述原理，利用MATLAB程序计算各位置单孔构造波形fj(t)按照对应延时的叠加合成，得到包含振速峰值、频率等信息的合成波形F(t)。

2.6 本文方法与传统方法对比

值得注意的是，本文方法所要解决的问题与传统方法有所不同。

在隧道爆破获取基础单孔波形方面，以往方法主要是获取单临空面下单孔波形作为基础波形函数，适用于第二临空面形成前的掏槽爆破振动波形构造和计算。本文为了研究第二临空面形成后的爆破振动规律，专门设计获取了双临空面条件的单孔波形，适用于第二临空面形成后辅助孔、周边孔的波形构造及计算。

在各炮孔波形构造方面，药量和爆心距是主要研究参数，但在爆破远区常忽略各炮孔的实际位置差异，针对爆破近区波形构造，本文对每个炮孔的实际爆心距进行了测算，并就爆破近区波形丰富的频率特征分解出不同频带子波进行分析构造，使构造波形在时域和频域上均更贴合实测波形。

3 现场爆破振动数据采集及特点分析

3.1 数据采集

按照图2设计进行现场爆破，实测现场爆破振动数据。由于X、Y、Z三个方向的爆破振动波形分析及构造方法相同，以X方向数据为例进行构造说明，Y、Z方向不再累述。图5为所测X方向振动波形，可从图中分离并获取双临空面条件下三个测点单孔爆破(MS5、MS7)振动波形。

3.2 频率分析及优势频带确定

从图5中截取MS5(116.5～173.5 ms)和MS7(200.5～240 ms)的单孔爆破波形，并截取MS11作为双孔爆破振动波形，截取960～1 065 ms电子雷管段作为微差爆破振动波形。

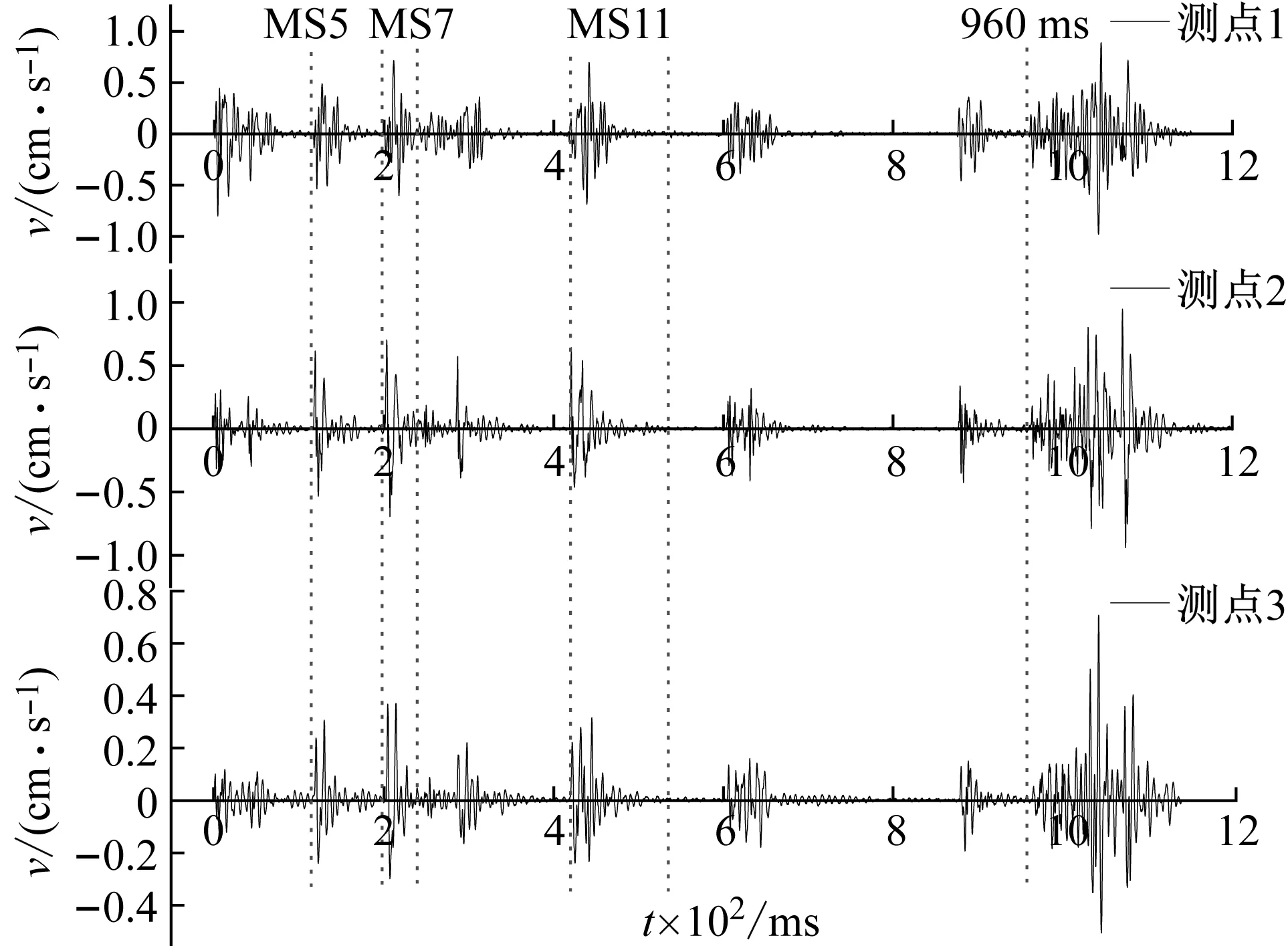
图5 各测点X方向实测振动波形Fig.5 Measured vibration waveform in X direction of three measuring points

由于采样频率为8 000 Hz，利用db5小波包对上述截取波形进行6层分解后，频带宽度达到62.5 Hz。利用式(1)、式(2)计算各频带能量占比。对能量占比小的高频频带进行适当合并，得到各类波形X方向能量分布情况,如表1所示。

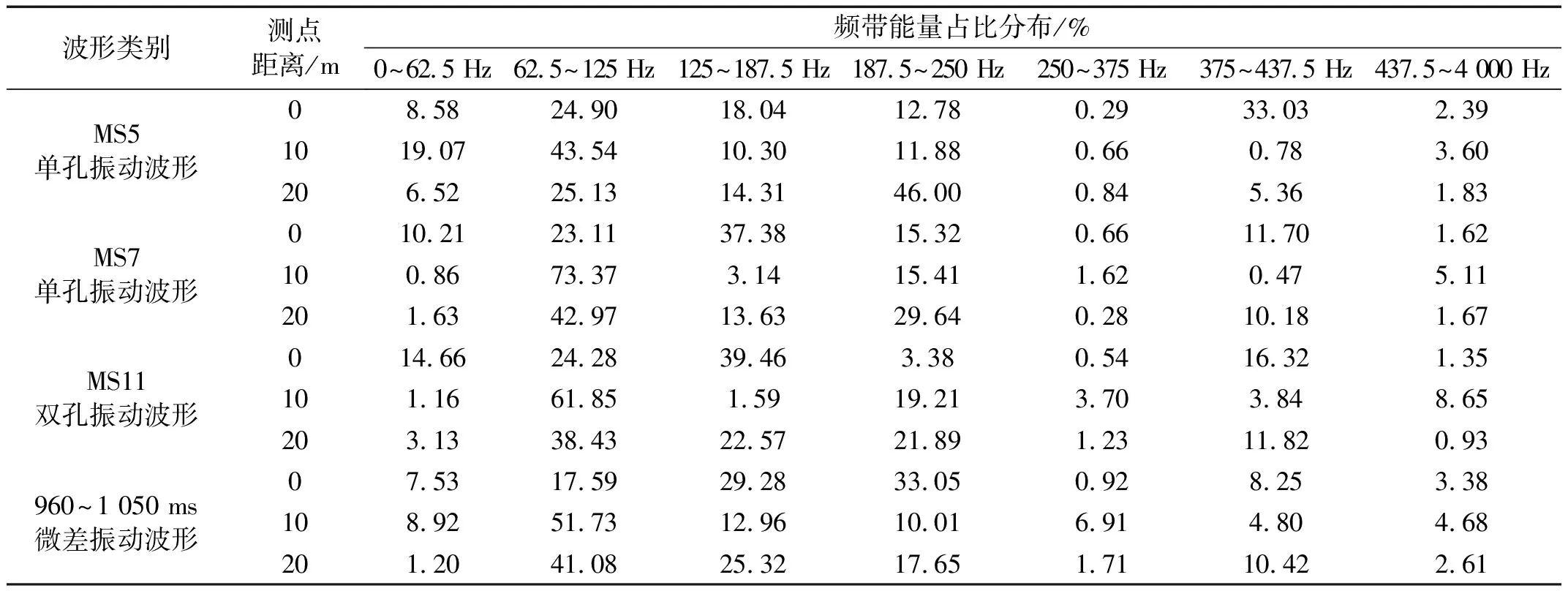
表1 X方向各类振动波形能量分布

由表1数据可知，各类波形大部分能量都集中在250 Hz以下的频带，但更高频带处(375～437.5 Hz)也存在能量的累积，这表现出爆破振动能量在频域上并不总是连续分布，还具有局部集中的特点，这一特征与其他文献研究结果一致。另外在0～187.5 Hz频带范围内，MS7单孔爆破与MS11双孔爆破在三个测点上的能量比例分布一致，但是和960～1 050 ms微差爆破的能量比例分布差异较大，可能是因为较短时间段内爆破炮孔数目的大量增多会影响到低频成分的占比。

总体而言，在爆心距变化不大的情况下，各炮孔能量的具体占比可能有所差异，但都稳定集中在某几个频带。在爆破近区，能量主要分布在0～62.5 Hz、62.5～125 Hz、125～187.5 Hz、187.5～250 Hz和375～437.5 Hz多个频带上。为避免划分优势频带过多造成个别频带子波振幅过小，进而影响子波振速衰减函数拟合，确定0～125 Hz、125～250 Hz、375～437.5 Hz为单孔波形的主要优势频带，重点分析单孔爆破振动在主要优势频带的子波振速变化规律。

3.3 优势频带子波振速分析

将三个测点的实测波形分别进行小波包变换得到上述三个优势频带的子波，如图6为测点1处X方向振动波形在各优势频带的子波。根据图2中的雷管布置可知，MS1炮孔爆破达到最大振速时尚未受到MS3的影响；960 ms炮孔的装药量(0.15 kg)过小，其对965 ms炮孔爆破最大振速的影响也可忽略。因此，可在各频带子波中提取MS1、965 ms处最大振速和MS5、MS7单孔爆破最大振速共同作为单孔爆破最大振速。统计各频带单孔爆破最大振速与对应炮孔的药量、爆心距数据如表2所示，以分析不同优势频带子波的最大振速变化规律。在MATLAB中对单孔药量、距离和各频带最大振速分析拟合，得到相应表达式(9)～式(11)。

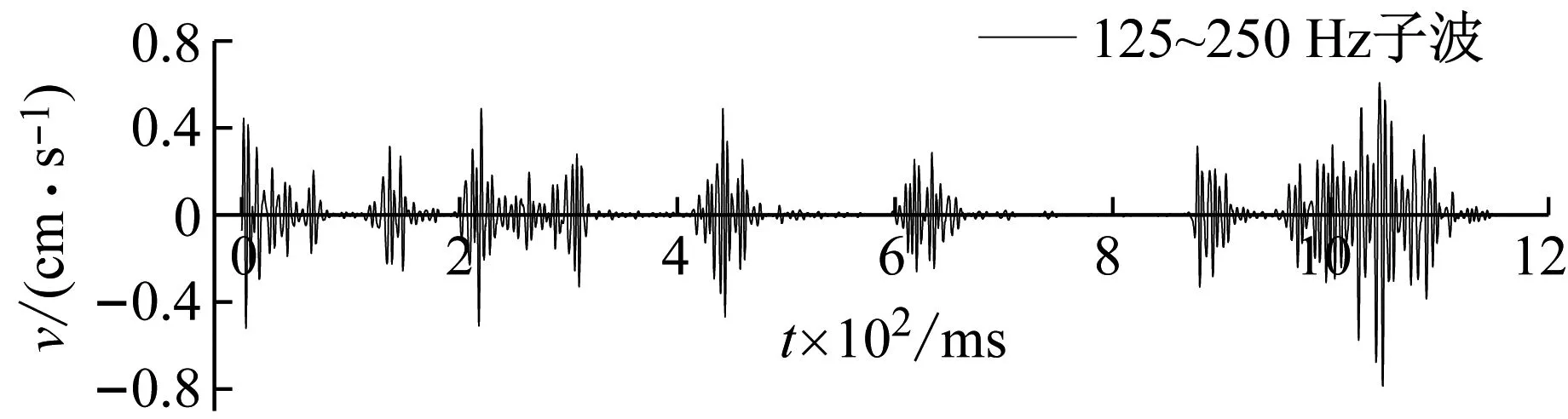
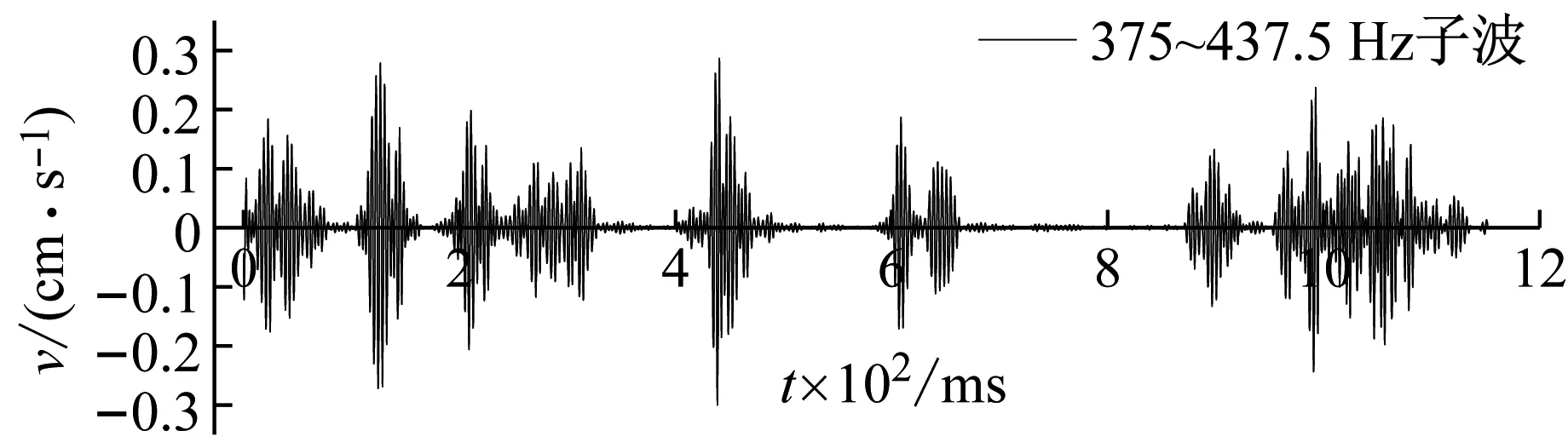
图6 测点1处X方向各优势频带子波Fig.6 Waveforms in main frequency ranges in X direction of point 1

表2 X方向单孔爆破相关参数Tab.2 Parameters of single hole blasting in X direction

v1=0.632 5Q1.831 9R-0.566 5

v2=0.998 8Q1.370 6R-0.655 5

v3=0.999 3Q0.406 8R-0.732 3

式中：v1、v2、v3分别表示0～125 Hz、125～250 Hz和375～437.5 Hz频带上子波的最大振速峰值。

在式(9)～式(11)中，装药量Q和距离R在不同频带的指数系数并不相同，药量的指数系数随着频率升高在减小，距离指数系数的绝对值随着频率的升高在增大，即不同优势频带子波的振速衰减规律不同。因此，考虑到不同频率爆破振动波衰减特征差异，在构造单孔波形时应先分别构造三个优势频带振动子波。

4 波形的构造、合成及应用

4.1 单孔波形的构造

上述分析已得到各优势频带最大振速衰减函数式，根据2.4节所述基于药量、距离变化调整各频带子波幅值大小，构造任意位置炮孔在各频带的子波，进而构造出单孔爆破振动波形。将式(9)～式(11)中所得指数系数代入式(6)，则炮孔在0～125 Hz、125～250 Hz和375～437.5 Hz三个优势频带上的子波构造函数为

f1,j(t)=(Qj/Q0)1.831 9·(Rj/R0)-0.566 5·f1,0(t)

(12)

f2,j(t)=(Qj/Q0)1.370 6·(Rj/R0)-0.655 5·f2,0(t)

(13)

f3,j(t)=(Qj/Q0)0.406 8·(Rj/R0)-0.732 3·f3,0(t)

(14)

按照式(7)进行叠加构造，得单孔构造函数式(15)

fj(t)=f1,j(t)+f2,j(t)+f3,j(t)

(15)

下面以构造965 ms处炮孔单孔波形为例。先选取MS5炮孔波形作为基础波形f0(t)，经过小波分解后得上述三个优势频带上的基础子波fi,0(t)(如图7)。将MS5、965 ms炮孔的药量、到测点1的距离代入式(12)～式(14)中，调整MS5各频带子波，得到965 ms三个频带子波，叠加得测点1处X方向构造波形(如图8)，构造波形峰值0.239 2 cm/s，与实际峰值0.333 4 cm/s相差不大。对构造波形进行傅里叶变换，得到频谱图(如图9)，可见构造波形有70 Hz、225 Hz等多个优势频率，与表1中的优势频带相对应。构造波形符合实际单孔波形的特点，因此可用此法构造各位置炮孔的单孔波形。

4.2 微差爆破振动合成

以MS5或MS7单孔波形为基础波形，按照上述波形构造方法可构造出X、Y、Z三个方向的各炮孔振动波形，表3为电子雷管区域各位置炮孔到近区测点(测点1)的水平距离Rxy、垂直距离Rz、爆心距R和药量Q。在MATLAB中按照设计的延期时间基于线性叠加原理对各炮孔构造波形进行程序叠加计算，得到各方向合成波形。图10～图12为测点1处三个方向的合成波形和实测波形的对比。

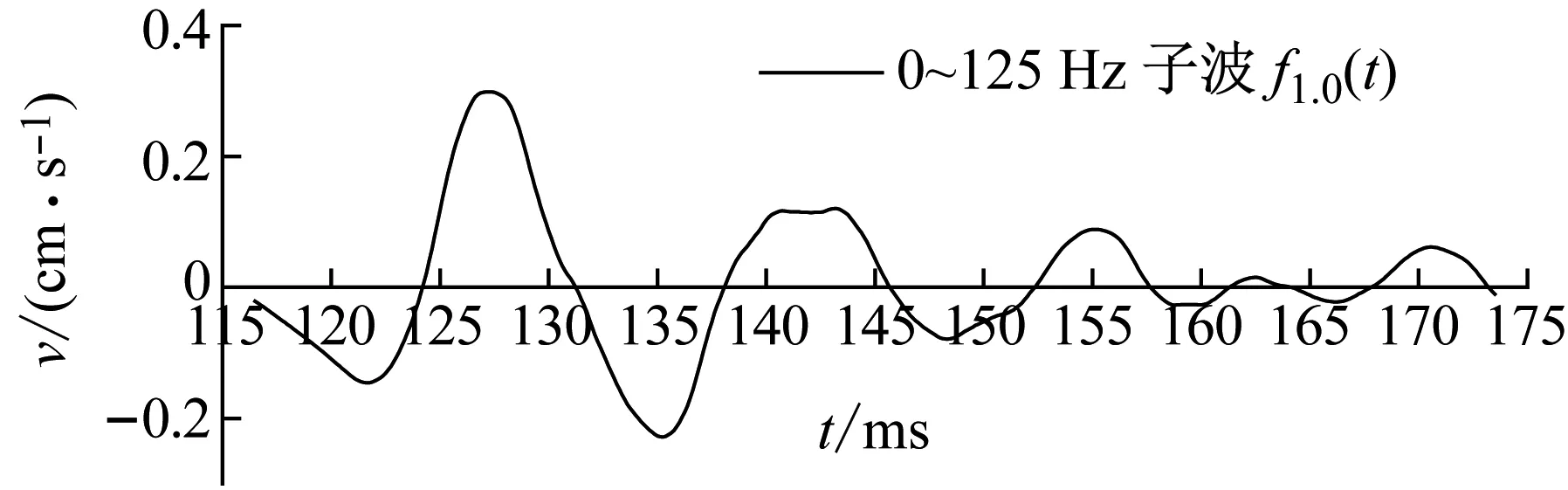
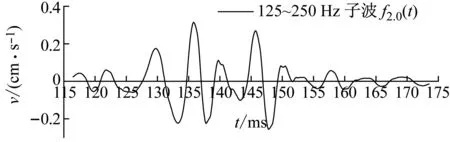
图7 MS5炮孔X方向各频带子波Fig.7 Waveforms of MS5 in main frequency ranges in X direction

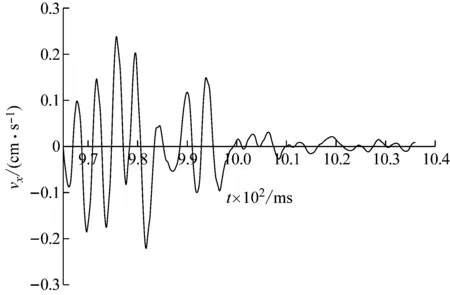
图8 965 ms炮孔X方向构造波形Fig.8 Constructed waveform of single hole at 965 ms in X direction

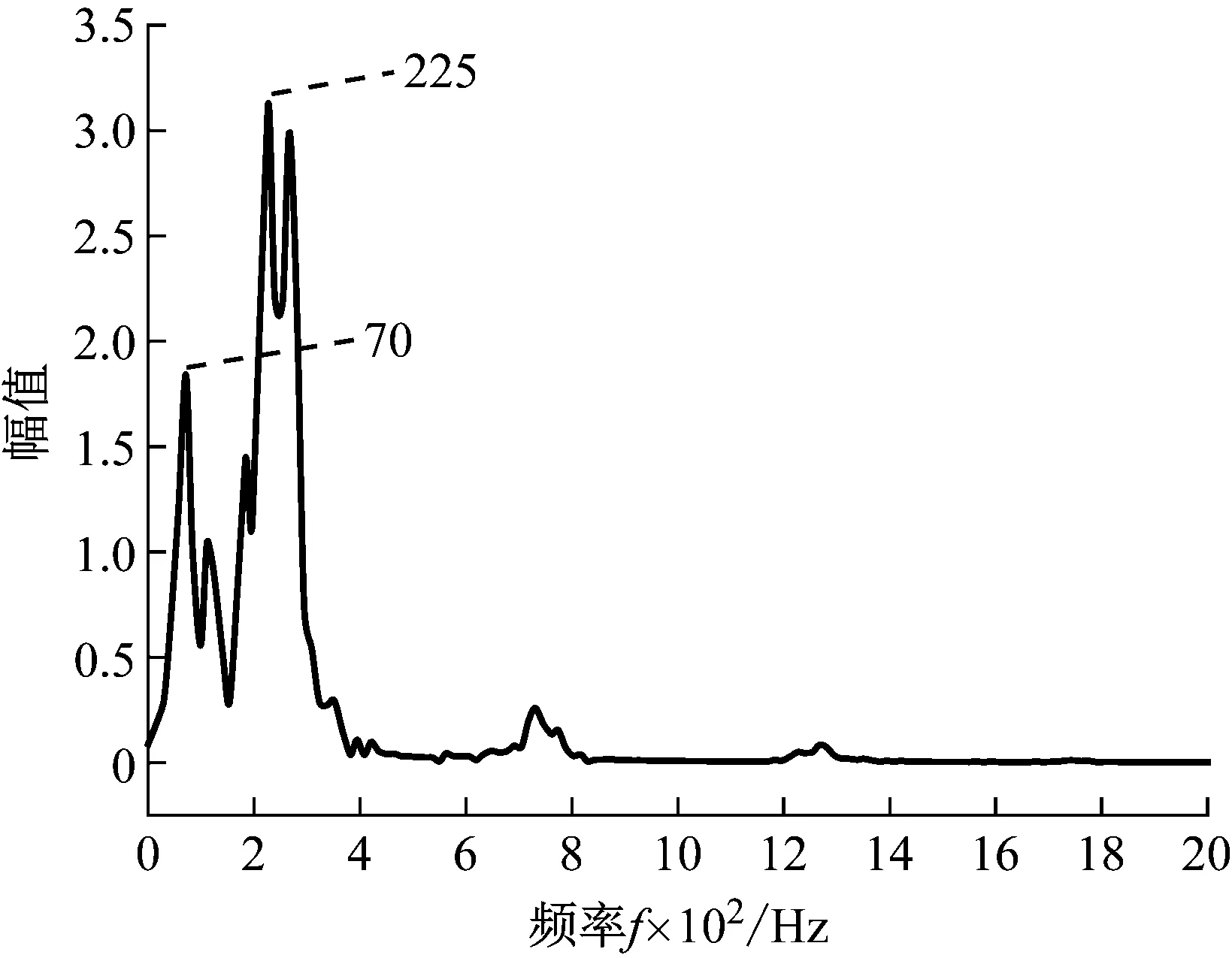
图9 965 ms炮孔X方向构造波形频谱图Fig.9 Frequency spectrum of constructed waveform of single hole at 965 ms in X direction

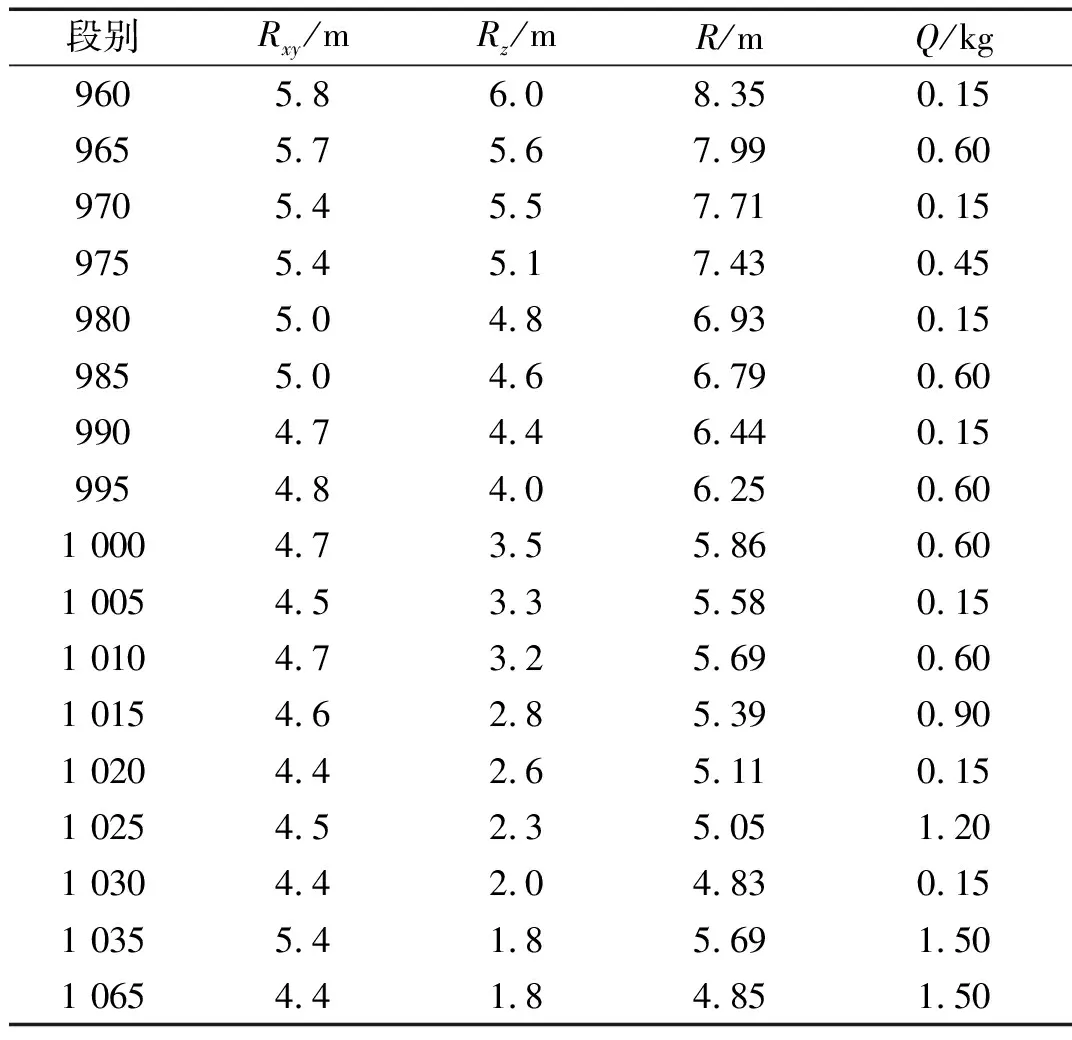
表3 电子雷管各炮孔爆破参数Tab.3 Blasting parameters of electronic detonator

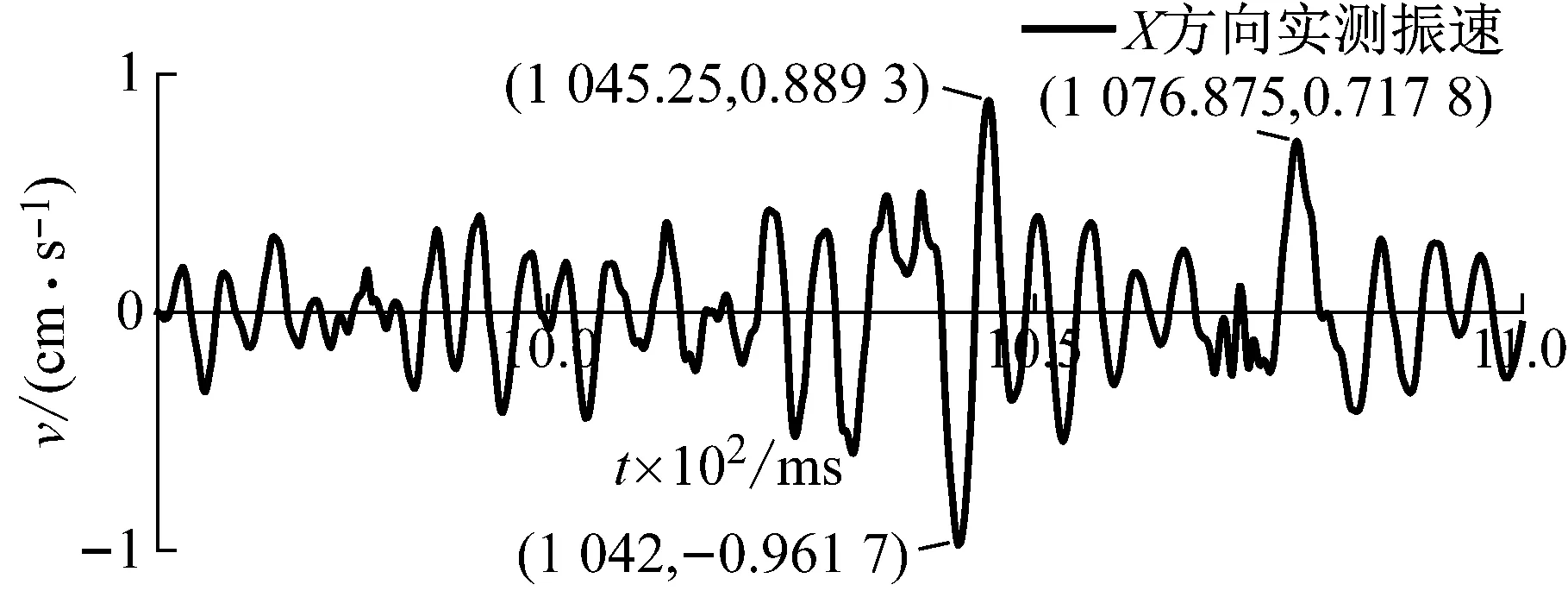
图10 测点1处X向960～1 065 ms实测与合成波形Fig.10 Measured and resultant vibration velocity waveforms of point 1 at 960-1 065 ms in X direction

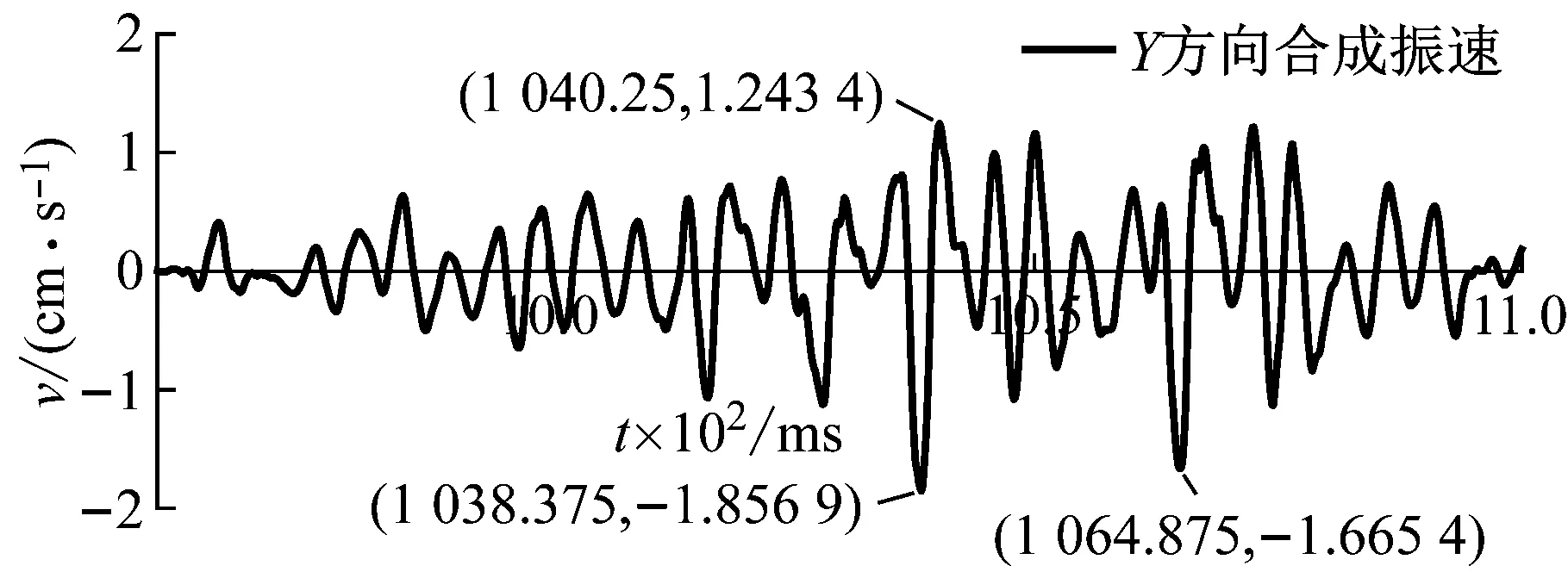
图11 测点1处Y向960～1 065 ms实测与合成波形Fig.11 Measured and resultant vibration velocity waveforms of point 1 at 960-1 065 ms in Y direction

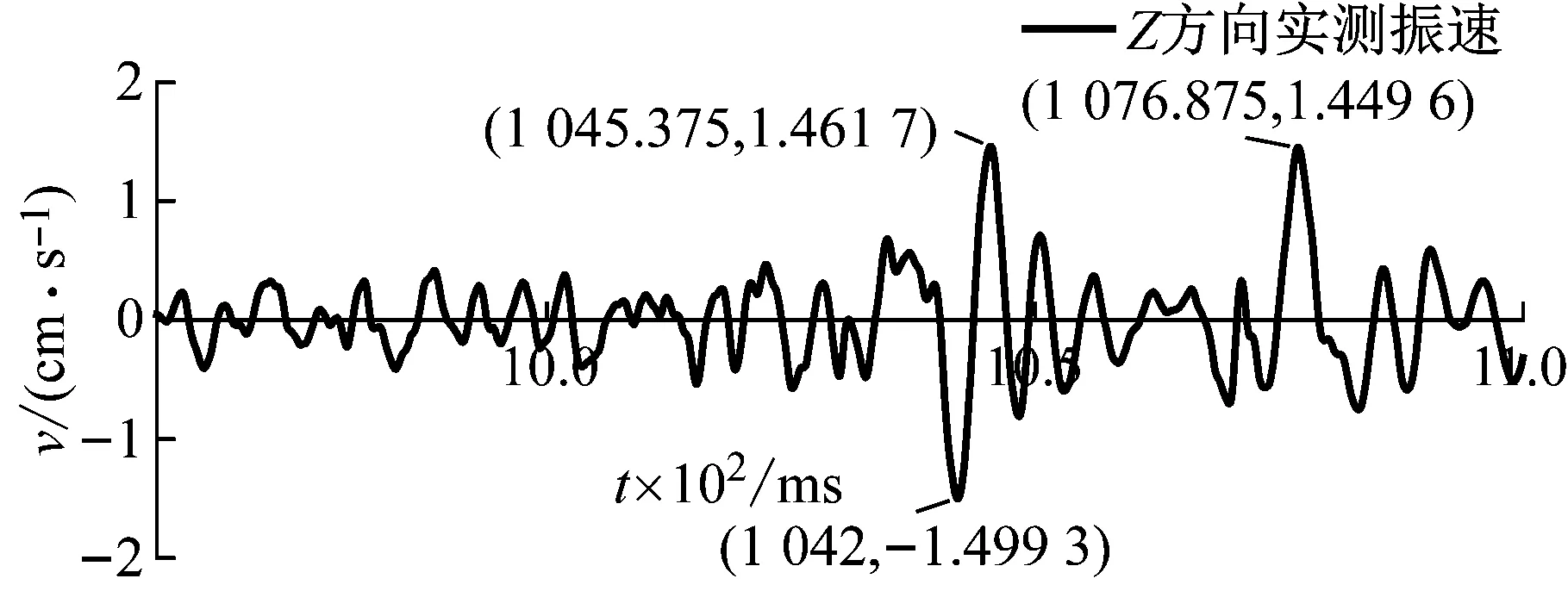
图12 测点1处Z向960～1 065 ms实测与合成波形Fig.12 Measured and resultant vibration velocity waveforms of point 1 at 960-1 065 ms in Z direction

对比叠加合成波形与实测波形，无论是峰值大小还是峰值出现时刻都吻合较好，主要振速峰值预测的绝对误差控制在0.3 cm/s以内。将合成波形和实测波形进行频谱对比，如图13所示，合成波形频谱曲线与实测波形频谱曲线的主频段相近。三个方向的计算结果都存在这一特点，说明设计双自由面获取单孔波形，并考虑到炮孔位置和频带差异来构造各炮孔波形，进而预测合成波形的方法可行，且准确度较好。

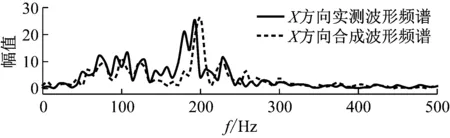
图13 测点1处960～1 065 ms实测波形与合成波形频谱Fig.13 Measured and predicted spectrums of waveform of point 1 at 960-1 065 ms

4.3 最优延期时差的确定

根据线性叠加原理可知，不同延期时差下叠加合成的振动波形峰值大小不同，因此存在一个最优延期时差，按照最优延期时差进行波形叠加所得合成波形的最大振速峰值较小。由于测振仪Z向与振动波传播方向垂直，受仪器布设时方位误差的影响较小，且该方向实测振速较大，因此下面根据Z向构造波形合成情况来确定最优延期时差。

根据上述原理，不改变各炮孔药量和爆心距，构造出电子雷管区域Z向的所有炮孔波形，并将相邻雷管的延期时差均设为同一变量Δt，在MATLAB中程序计算Δt取不同数值时(Δt=1,2,…,20 ms)最近测点处(测点1)的电子雷管合成波形。图14为电子雷管相邻延期时差Δt为6 ms、7 ms、8 ms时的合成波形。记录各延期时差下所得合成波形的最大振速峰值，统计得到图15。

(a) Δt=6 ms

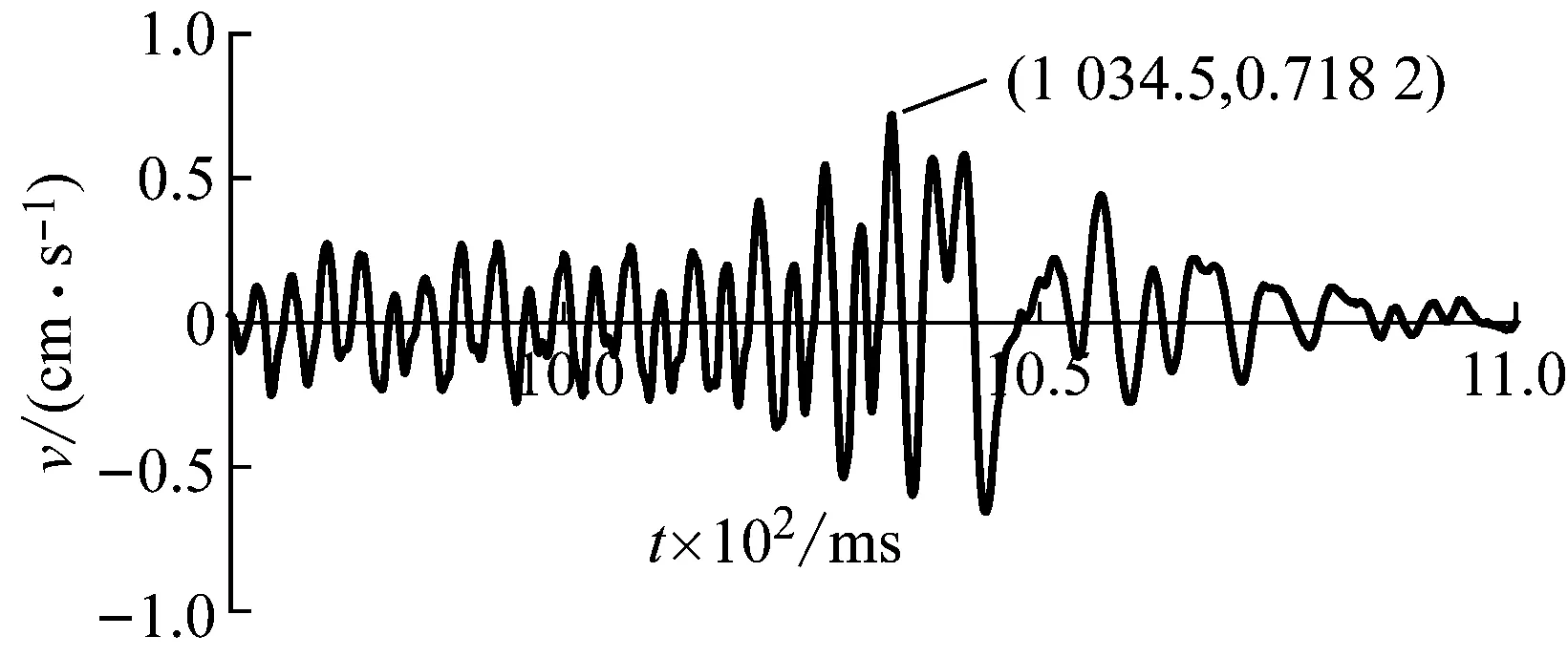
(b) Δt=7 ms

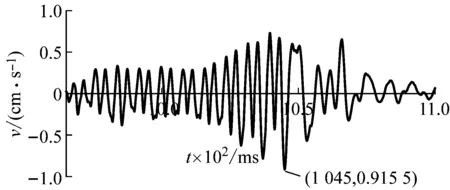
(c) Δt=8 ms图14 电子雷管Z向不同延期时差下叠加合成波形Fig.14 The synthetic waveforms with different delay intervals in the Z direction of the electronic detonator

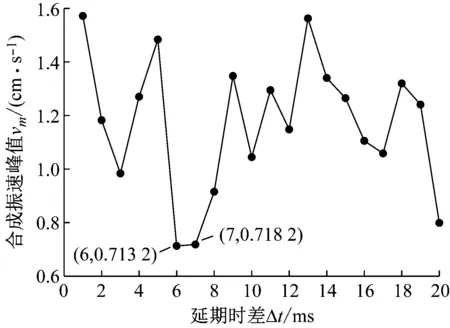
图15 不同延期时差下的振速峰值Fig.15 The peak vibration velocity at different delay intervals

图15显示，计算合成的最大振速峰值随延期时差的增大具有一定的起伏变化，这主要是受延期时差和爆破振动主周期之间数值关系的影响。当延期时差在6～7 ms时，合成波形的最大振速峰值是20 ms范围内的较小值。因此，当周边孔参数不变时延期时差为6～7 ms时的减振效果最优；此外还可同时调整药量、延期时差等多个爆破参数实现爆破振动控制。

为验证以上结论，在随后的莲塘隧道II区数次爆破中，采用孔间延时6～7 ms进行试验，爆破近区实测振速特征值及出现时间与预测值均非常接近，实测峰值均小于0.9 cm/s，振速控制效果良好。

5 结 论

(1) 在现场试验、单孔波形重构和程序计算基础上，建立了第二临空面形成后计算任意位置炮孔微差爆破合成振速的方法，解决了目前只能计算第二临空面形成前较短时段爆破合成振速的难题，为精确确定爆源近区爆破参数提供了途径。

(2) 在单孔波形构造中将炮孔距离、药量作为构造参数，同时考虑了优势频带对波形振速的影响，以有限实测单孔波形构造爆区不同位置炮孔单孔振动波形，减小了波形构造时未考虑频域因子带来的误差，具有简便灵活、适用性强的优点。

(3) 莲塘隧道应用结果表明：计算合成振动曲线与实测振动曲线吻合程度较高，振动峰值绝对误差在0.3 cm/s以内；通过改变延期时差计算相应合成振动曲线，确定了II区周边孔电子雷管的最优延期时差等爆破参数，并在随后爆破测试中得到验证。