关于函数连续性的研究

黄娟霞

在高等数学中，函数连续的概念具有承上启下的作用，它是在极限概念的基础上建立的，对零点定理、介值定理等重要定理的学习具有重要的意义，并为后续的导数、微分和积分的学习奠定了基础，反过来，研究可导、可微和可积的性质又可以进一步加深对函数连续概念的掌握和理解［1-4］.

1 函数连续性的概念

1.1 函数在一点的连续性

定义1［5］设函数y=f(x)在点x0的某一邻域内有定义，如果，那么就称函数y=f(x)在点x0处连续.

定义2［5］设 Δx=x-x0，函数y=f(x)在点x0的某一邻域内有定义，在此点处函数取得增量，若 有Δy→0(当Δx→0），那么就称函数y=f(x)在点x0处连续.

定义 3［5］对ε＞0 ，若 ∃δ＞0 ，使得当时，有，那么就称函数y=f(x)在点x0处连续.

1.2 左连续和右连续

定义 4［5］如果，则称函数f(x)在点x0左连续.如果，则称函数f(x)在点x0右连续.

定义5［5］设函数y=f(x)在点x0的某一邻域内有定义，如果，那么就称函数y=f(x)在点x0连续.

1.3 函数在区间上的连续性

定义6在开区间(a,b)内每一点都连续的函数，称为在开区间(a,b)内的连续函数.如果函数在开区间(a,b)内连续，且在左端点a右连续，在右端点b左连续，那么称函数在闭区间[a,b]上连续.

2 函数的间断点

定义7设函数y=f(x)在点x0的某一邻域内有定义，如果，那么就称x0为函数y=f(x)的间断点.

从定义5可知，连续与间断是一对相对立的概念，函数不连续即间断.因此，函数在下列三种情况下出现间断：

（1）在点x=x0没有定义.

（2）虽在x=x0有定义，但不存在.

（3）虽在x=x0有定义，且存在，但

函数的间断点详细可划分为：

例1设函数f(x)的表达式为

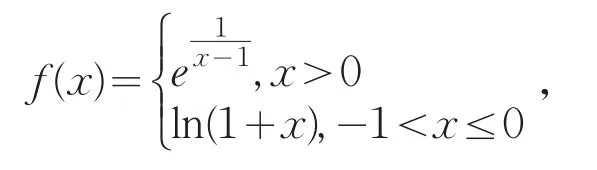
试确定函数间断点的类型.

解 函数间断点为x=0,x=1.

当x=0时 ，，，从 而x=0为 函 数的跳跃间断点，也即为第一类间断点.

当x=1时，，，从 而x=1为 函 数f(x)的无穷间断点，也即为第二类间断点.

3 漏斗原理

函数的连续、可导、可微和可积这四个概念的关系恰好形成一个“漏斗”，称为漏斗原理.如图1所示.

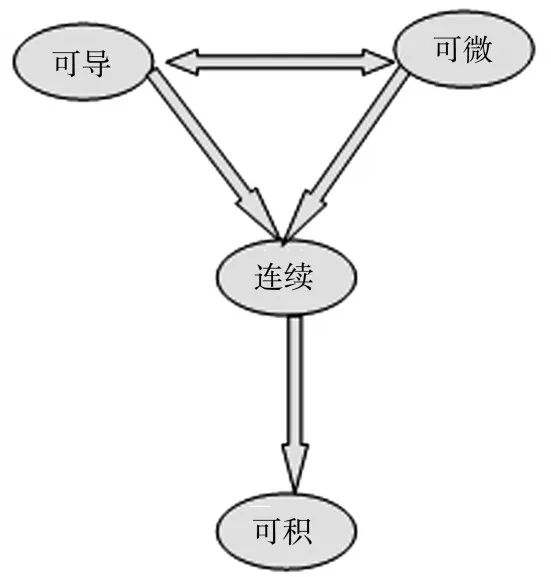
图1 漏斗原理

定理1函数f(x)在点x0可导的充分必要条件是函数f(x)在点x0可微.

证明（必要性）如果f(x)在点x0可导，即存在，根据极限与无穷小的关系，上式可写成，其中α→0（当Δx→0），由此，且不依赖于Δx，所以f(x)在点x0也是可导的.

（充分性）如果函数f(x)在点x0可微，则按定义有Δy=AΔx+αΔx，此式两边除以Δx，得

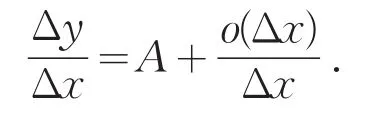
于是，当Δx→0时，由上式就得到

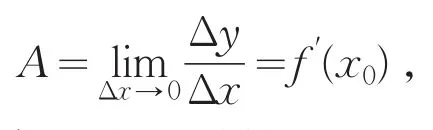
所以f(x)在点x0是可导的.

定理2如果函数f(x)在点x可导，那么函数f(x)在点x处必连续.

证明 如果函数y=f(x)在点x处可导，即存在.则

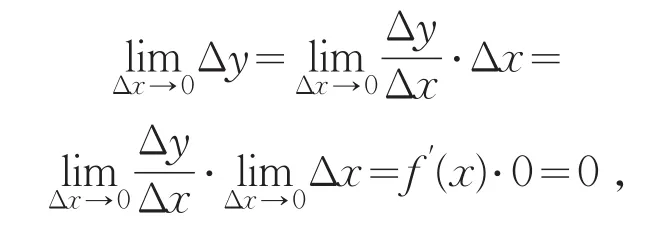
即函数y=f(x)在点x处是连续的.

注：定理2中连续是可导的必要条件，即函数f(x)在点x处连续却不一定可导.

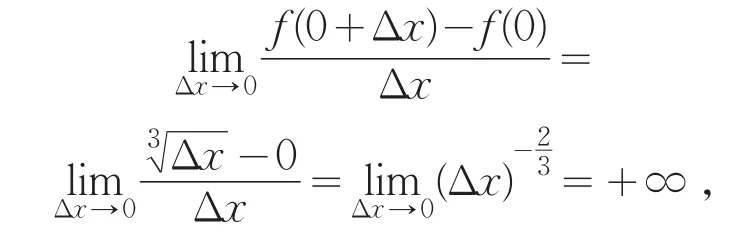
定理3如果函数f(x)在[a,b]上连续，那么函数f(x)在[a,b]上可积.

证明 由于f(x)在[a,b]上连续，因此在[a,b]上一致连续.即对任给ε＞0，存在δ＞0，对 [a,b]中任意两点只要，便有

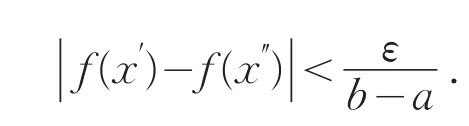
所以只要对[a,b]所做的分割T满足‖‖T＜δ，在T所属的任一小区间Δi上，就能使f的振幅满足

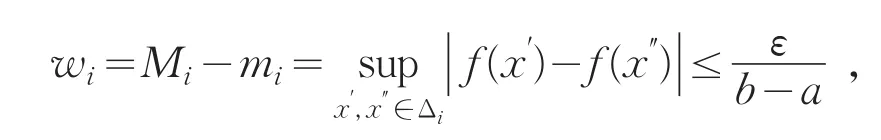
注：定理3中的连续是可积的充分条件，即函数f(x)在点x处可积却不一定连续.

例3讨论黎曼函数

在区间[0,1]上的连续性和可积性.

解 因为黎曼函数f(x)在x=0,1，以及(0,1)内的无理点处是间断的，因此黎曼函数不连续.

下证黎曼函数f(x)在区间[0,1]上可积.

任给ε＞0，在[0,1]内使得的有理点只有有限个，设它们为r1,r2,…,rk.现对[0,1]作分割T={Δ1,Δ2,…,Δn} ，使并把T中所有小区间分为和两类.其中为含 有中点的所有小区间，这类小区间的个数m≤2k（当所有ri恰好都是T的分割点时才有m=2k）；而为T中所有不含中点的小区间.由于f(x)在上的振幅于是

而f(x)在上的振幅于是

把这两部分合起来，则

即f(x)在区间[0,1]上是可积的.当取ξi全为无理点时，使得，于是

4 结论

连续性是函数最基础的性质之一，它对后续知识的学习至关重要.本文首先研究了连续的概念，然后通过对间断的研究来加深对连续的理解，最后通过漏斗原理对连续、可导和可积这三个微积分中最重要的概念进行对比说明.除此之外，还可通过对最值定理、零点定理及介值定理等知识的学习加深对函数连续性的理解.