赋Orlicz范数的Orlicz序列空间的k一致凸点

段丽芬，杨德清，陈洪亮

自1979年，Sullivan［1］引入局部k一致凸的概念以来，因其不但与空间的自反性、超自反性和正规结构等理论密切相关［2］，而且在逼近论等领域有重要应用得到关注［3-6］.同时，针对Orlicz函数空间而言，与其相应的点态性质的刻画都已获得［7-8］.赋Luxemburg范数Orlicz序列空间的k一致凸点判据也已查明［9］.本文对赋Orlicz范数Orlicz序列空间的k一致凸点展开研究，得到了赋Orlicz范数的Orlicz序列空间的k一致凸点的判别准则.

1 预备知识

设X是Banach空间，X′是其共轭空间，S(X)表示X的单位球面.

定义1［7］x(0)∈S(X)被称为k一致凸点是指若则其中

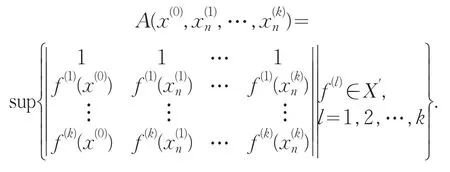
如果S(X)上每一点都是k一致凸点，则称X是局部k一致凸的.

定义2［4］若非负函数M是偶的连续凸函数，并且满足则称映射M:R→[0,∞)为N-函数.

用M(u)、N(v)表示一对互余的N-函数，p(u)为M(u)的右导数.M∈Δ2指存在常数c＞0，使得M(2x)≤cM(x)对较小的x成立.M∈∇2⇔N∈Δ2.称闭区间[a,b]为M的线性区间是指M在[a,b]上是线性的，但对任何ε＞0，M在[a-ε,b]和[a,b+ε]上都不是线性的.用{ }[ai,bi]i表示M的线性区间全体，记

定义p-(v)为：p-(0)=0,p-(v)=sup{p(u):0≤u＜v}(v＞0).线性集

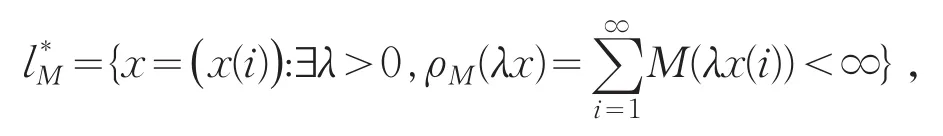
2 主要结果

定理1设M是N-函数，是k一致凸点的充要条件是：

（i）M∈Δ2⋂∇2；

这里h0满足

证明 必要性.因k一致凸点必为k强端点，利用文献［10］的定理1和定理3，只需证明M∈∇2及（ii）之（1）和（2）式即可.

首先证明M∈∇2.若不然，则存在正数列vn↓0，满足

取正整数mn,使得mnN(vn)≤1/nk＜(mn+1)N(vn).因M∈Δ2，可找到足够大的in,使得

令

则

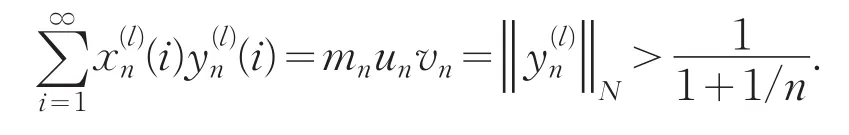
但由于对一切l=1,2,…,k,都有

其次证明（ii）之（1）式.若不然，则存在h0∈H(x（0）)和j∈N，使得，但

这里[a,b]为M的线性空间.文献［4］定理1.80指出，v∈LN是x（0）的支撑泛函的充要条件是ρN(v)=1 ，且

因此

但可取f(s)∈lN(s=1,2,…,k)，使得

则

产生矛盾.（ii）之（2）式可类似证得，不再赘述.

因M∈Δ2⋂∇2，所以自反，的有界元列存在弱收敛的子列，仍记为，设因M∈Δ2，则具有H性 质 ，进 而，且

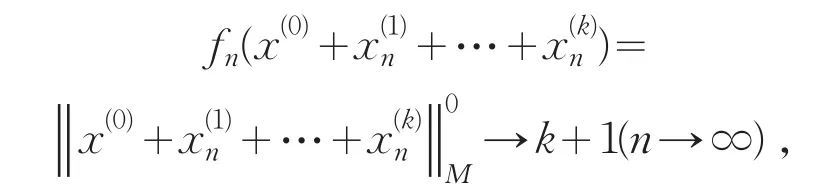
即

故

考虑到A(x(0),x(1)n,…,x(k)n)的连续性及（4）式有

若记h=,其中h0∈H(x(0)),hl∈H(x(l))(l=1,2,…,k),则

于是，对一切i∈N，都有

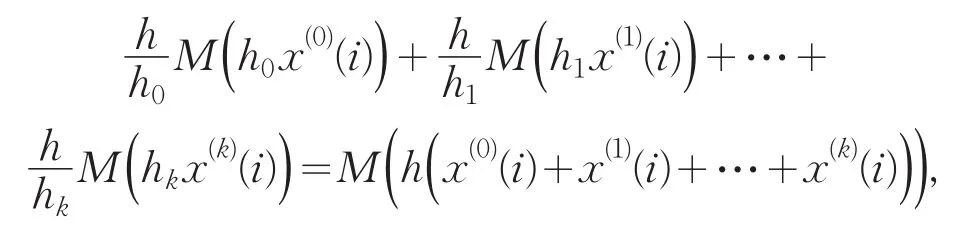
故对一切i∈N，h0x(0)(i),h1x(1)(i),…,hkx(k)(i)都在M的同一线性区间.

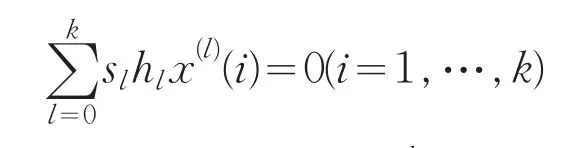
有非零解，记为(s0,…,sk),便有

当μ{i∈N:h0x（0）(i)∈RSM}≤k-1 时，可假定I={i∈N:h0x（0）(i)∈RSM}={1,…,k-1}. 则当i≥k时，因h0x(0)(i),h1x(1)(i),…,hkx(k)(i)都在M的同一线性区间，可类似文献［11］分四种情况 推知h0x（0）(i)=h1x(1)(i)=…=hkx(k)(i)(i≥k).结合齐次线性方程组

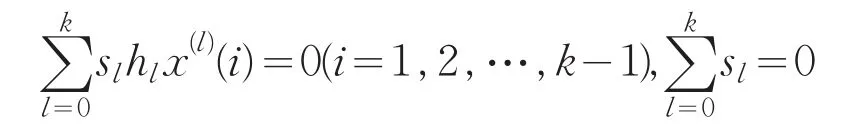
也有非零解(s0,…,sk),便有这说明无论条件中的哪种情况成立，都可得到线性相关的结论，从而A(x(0),x（1）,…,x(k))=0,与（5）式产生矛盾.

由定理1立即可得定理2.

定理2设M是N-函数，l0M是局部k一致凸的充要条件是M∈Δ2⋂∇2且M在[0,πM(1/k)]上严格凸，其中 πM(α)=inf{t＞0:N(p(t))≥α}.

3 结论

论文给出了由N-函数生成的赋Orlicz范数的Orlicz序列空间的k一致凸点的一个判别准则，进而得到了该空间局部k一致凸的一个充要条件.