高中数学教师教材使用情况个案研究*

贵州省铜仁学院(554300) 李明星 颜宝平 宋运明

《普通高中数学课程标准(2017年版)》标准中对教材的编写提出了新的建议,建议中指出：“教材的编写要有利于教师实现教学建议中对教师教学提出要求.要便于教师把握知识本质,驾驭课程内容;要便于教师把握知识结构,统筹教学安排;要便于教学设计,创设教学情境、提出合适的问题、有效组织教学;要为教师自主选择、增补和调整教学内容预留必要空间”.[1]但新教材仍在编制当中,教师使用的还是旧教材,一线的新教师对于教材的自主选择、知识的增补和调整是如何把握的? 有经验的教师又是如何把握的? 在新教材与旧教材的这个过渡阶段就需要有经验的教师来带领,因此研究高中数学教师在现阶段使用教材的情况,可以对其他新入职的数学教师提供参考.并期望在一定程度上或者在一定范围上引起其他教师在思想上的共鸣.

1 研究设计

研究方法采用个案研究法、访谈法、观察法、文本分析法,对两位教师进行基本信息的了解,取得两位教师的信任,通过录像观察他们在课堂上使用教材的实际情况.

1.1 研究对象

研究对象是G 省T 市的一所示范性高中的高二年级的两位教师, 第一位是具有高级职称且教学经验丰富的教师,在文章中我们成为A 教师,A 教师具有15年的教学经验,毕业于一所综合性的大学,所学专业为数学与应用数学,A 教师在教学中有着优异的教学成果.第二位我们称为B 教师,B 教师毕业于一所师范类院校的数学专业,具有4年的教学经验,具有中教二级职称的教师.两位老师所教的班级均为高二年级理科班,学生的层次属同一水平.

1.2 研究过程

研究内容是人教A 版选修2-1 第二章圆锥曲线与方程,该模块是研究几何学的重要课题之一,其借助坐标的方法来研究这部分内体现了解析几何中重要的数形结合思想,同时这部分知识也是学生深入学习数学的重要基础.研究从教学计划、数学问题、知识点个数与思想方法三个一级维度对教师使用教材进行分析,其中教学计划分为教学顺序、课时安排、以及教学思路;数学问题分为例题(例题内容和解题程序)、练习题内容、探究与思考;知识点个数、思想方法,分为：化归、类比与归纳、方程、函数、数形结合、算法化六个思想方法.

1.2.1 教学计划

(1) 教学顺序

对教材的结构顺序进行梳理得到图1：

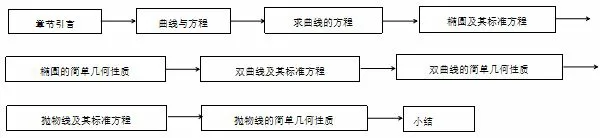
图1 教材顺序图

通过课堂实际观察,A 教师的教学顺序除了没有小结之外,其他环节都和教材一样,B 教师没有小结和章节引言,两位教师都没有小结的原因是收到了学校制度的影响,学校进行半期考试,导致两位教师没有时间进行总结.在对A、B 教师进行访谈之后得到B 教师没有进行引言的讲授是因为时间的限制还有B 教师自身的因素.A 教师讲解引言是因为想让学生明白什么叫圆锥曲线,学了这一章节,要懂得它的由来、概念、性质以及在生活中的应用.新课标中提到高中数学课程的学习,要不断提高学生的实践能力,认识数学的科学价值、应用价值文化价值和审美价值.

(2) 课时安排

课时安排将参考教师教学用书上的课时分配与实际课堂中教师所使用的课时,对两位教师进行观察分析得到表1：

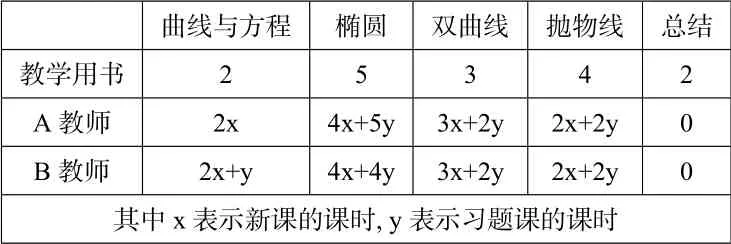
表1 课时分配表

由上表可知,两位教师在课时安排上差异不大,但与教师教学用书相差较大.在椭圆这一节使用了9 个课时,教学用书建议5 个课时,两位教师认为学生是第一次接触圆锥曲线,在新授内容上要讲解的很细致,特别是概念的形成,对于高中数学来说,所有的题型都是来源于基础知识的变式,只有掌握牢固的基础知识,才能进一步的学习基础知识的拓展,而掌握牢固的基础知识,则在于对概念的理解,在掌握概念的基础上,才能进一步对概念的本质和相关性质的理解.A、B 两位教师在教学上都是一节新课一节习题课,习题课是对上一节新课内容的巩固,主要是因为学生的基础,教师从作业、课上的反应情况来调整自己的课时安排,例如B 教师在曲线与方程发现学生对概念的理解不够,没有马上进行下一节内容的讲解,而是给学生加了一节习题课巩固概念.

(3) 教学思路

教学思路是教师根据学生的实际情况和教材内容而制定的,教师的教学思路简称为教的思路,教材的知识发展思路简称为教材思路.由于篇幅,这里以椭圆的标准方程为例：

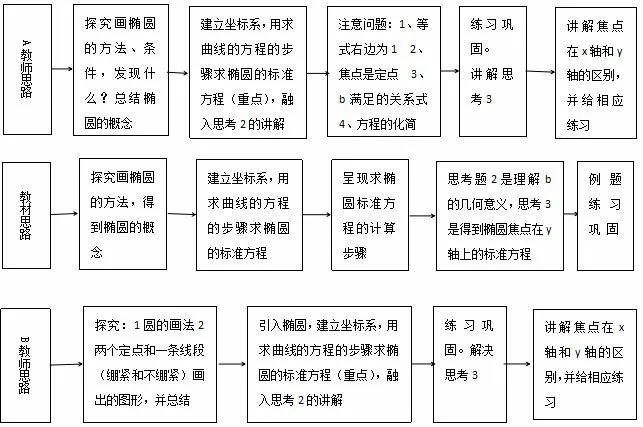
图2 椭圆及其标准方程思路图

从教材的思路上看,通过探究椭圆的画法—椭圆概念—求椭圆的标准方程—练习巩固.在内容上b 值的几何意义理解和焦点在y 轴上的椭圆标准方程的探索是作为两个思考题来进行处理.A 教师和B 教师对思考2 都是融入椭圆的标准方程的推导之中,思考3 都作为第二课时内容来处理.A教师在概念的引入上和教材一样,B 教师则有不同,B 教师是通过圆的画法是通过一个动点、一个定点和一条绷直的定直线得到的,思考如果是一个动点和两个定点,线段绷直和不绷直的状态将会是怎样? 将问题抛给学生,引发学生的求知欲望,即得到本节课的主题,椭圆的概念.在后面的椭圆的第二概念和直线与圆锥曲线的位置关系学习中,教材中是通过两个例题来呈现的,A、B 两位教师则是以知识点的形式来进行讲解.

首先,A、B 教师能够把教材中例题总结成为知识点对学生进行讲授,使得学生更加的重视,这样做的原因是高考对于知识点的考察侧重点不同,教师在教学中讲解内容的侧重点也不同.比如圆锥曲线的第二定义和直线与圆锥曲线的位置关系,由圆锥曲线第二定义可以得到焦半径公式,对于很多题可以快速解决,直线与圆锥曲线的位置关系在高考中处于一个比较重要的部分,但是难度略大,特别是方程的化简,因此,高考是影响教师对教材处理的原因之一,教师对教材内容使用的侧重点取决于高考对知识点的考察方向.

其次,在新授课的引入方式上,A、B 教师和教材各有不同,A 教师在引入上会使用教材给出的信息技术,但都是一些简单的PPT 动画,B 教师没有信息技术的使用.学校具有使用几何画板等信息技术软件的条件,但是都没有安装几何画板等数学软件,只有简单Word、PPT、Excel 办公软件.

最后,在教学方式上,A 教师对于教材上内容处理更为细致,一是考虑到学生的因素,以学生为教学的活动中心,突出学生的主体地位,二是教师自身的因素,A 教师仔细研读课标,上课时会融入一些课标的理念,培养学生的学科素养.B 教师是以高考训练为主,通过训练让学生的双基更为扎实,此外B 教师在知识点的衔接上处理得更好.

1.2.2 数学问题

问题是数学的心脏.数学问题甚至影响着教学的好坏,本节内容中以数学问题作为观察的单位,了解教师在教学中呈现的数学问题方式和教材内容的一致程度.其中数学问题内容是指教师使用的数学问题和教材的一致程度(包括例题和练习题),呈现方式是指数学问题的解题程序的一致程度,呈现方式只有例题有.两者都分为和教材完全相同、大部分和教材相同少部分自行设计、少部分和教材相同大部分自行设计、完全和教材不同,此划分是根据台湾学者徐伟民测量教师忠实度所采用的计算方法,主要是透过两个不同的系数来了解教材使用的忠实度TCT(Task Content Taught)和TPT(Task Procedure Taught),TCT 和TPT 是指教师完全按照教材中的数学问题内容和呈现方式来进行教学的程度.TCT 和TPT 越接近1,表示教材使用的忠实度越高,教师对于教材的改编就越大,反之,教师对教材的改编就越小.(强调问题内容的一致程度),(强调解题程序的一致程度)

表2 TCT 和TPT 计算表

根据TCT 和TPT 的计算表得到两位教师忠实度统计表

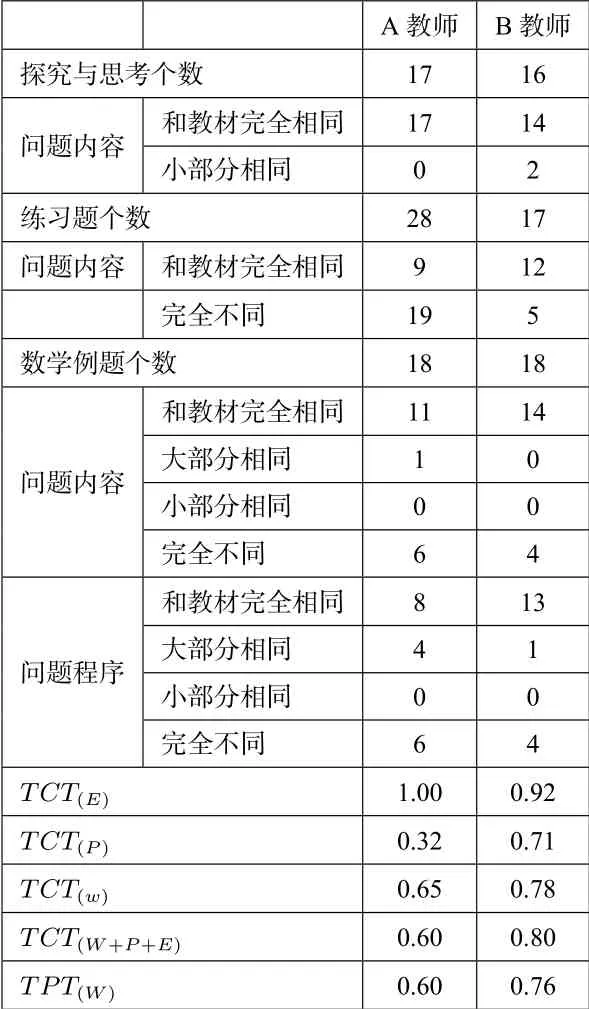
表3 TCT 和TPT 统计表

注：TCT(E)指探究与思考的TCT 值, TCT(P)指练习题的TCT 值, TCT(W)指数学例题的TCT 的值,TCT(W+P+E)指探究与思考、练习题和例题的TCT 值,TPT(W)指数学例题的TPT 值.

(1) 数学例题

教材中数学例题分为题目(数学问题)和解题程序(解题过程),A 教师的TCT(W)的值为0.65,B 教师的为0.78,相差0.13.A 教师使用的数学问题的忠实度比B 教师的低,从使用的数学问题上来看,A 教师的TCT(W+P+E)忠实度为0.60,B 教师为TCT(W+P+E)为0.80.对于数学例题和解题程序,A 教师根据个人的经验对题目进行一题多解,变式训练等.

(2) 练习题

教材中共有29 个练习题,A 教师使用的数学练习题有28 个,使用的数学练习题和教材完全相同的有9 个,有19 个完全不同.B 教师使用的练习题有17 个,12 个完全和教材相同,5 个完全不同.A 教师的练习题的TCT(P)为0.32,说明A 教师在练习题的使用上小部分忠实于教材,B 教师为0.71,A 教师在练习题的TCT 与教材相差较大,根据课堂观察A教师对于改动较大的是,每学习完一个新的知识点,A 教师就会在黑板上出相应的练习题给学生练习,根据学生的掌握情况做出相应的教学活动的变化.

(3) 探究与思考

探究与思考在教材中呈现的方式为探究、思考、探究与发现三种, 教材中共有26 个探究与思考, A 教师使用了17个,B 教师使用了16 个.从总体上看,A 教师和B 教师探究与思考的使用上趋向于和教材一样(TCT 值都在90%以上),A 教师对于探究与思考的TCT(E)值为1,完全忠实于教材,对于探究与思考,A 教师认为问题本身没什么可改变的,关键是要会挖掘问题背后的意图.

1.2.3 知识点个数与思想方法

(1) 知识点个数

知识点是知识中最小的单位、最具体的内容,本文根据课标、数学教师教学用书以及教材等资料,圆锥曲线与方程知识点划分如下29 个曲线与方程：曲线与方程的概念、求曲线的方程步骤.

椭圆：椭圆的定义、椭圆焦点在x 轴的标准方程、椭圆焦点在y 轴的标准方程、椭圆的范围、椭圆的对称性、椭圆的顶点、椭圆的离心率、直线与椭圆的位置关系(隐性)、椭圆第二定义(隐性).

双曲线：双曲线的定义、双曲线焦点在x 轴的标准方程、双曲线焦点在y 轴的标准方程、双曲线的范围、双曲线的对称性、双曲线的顶点、双曲线的离心率、双曲线的渐近线、双曲线第二定义(隐性)、直线与双曲线的位置关系(隐性).

抛物线：抛物线的定义、抛物线的4 种形式的标准方程、抛物线的范围、抛物线的对称性、抛物线的顶点、抛物线的离心率、抛物线的弦长公式(隐性)、抛物线与直线的位置关系(隐性).

A 教师在讲授了上面的29 个知识点之外还讲授了椭圆和双曲线的弦长公式、椭圆的焦点弦公式、焦半径公式、双曲线的焦点弦公式、焦半径公式、抛物线的通经、抛物线的焦半径、抛物线的焦点弦公式、利用点差法求中点弦所在直线的斜率.比教材上的知识点多了9 个,其中,椭圆和双曲线的焦点弦、焦半径公式是通过它们的第二定义推导出来的,弦长公式又是直线与圆锥曲线关系中常用的,在教材中的练习题中对于弦长公式也有体现.

B 教师在知识的拓展上相对A 教师较少,只讲解了椭圆与双曲线的弦长公式、利用点差法求中点弦所在直线的斜率、椭圆的焦半经、抛物线的焦点弦长公式共4 个,比A 教师少了5 个知识点,很明显A 教师对知识的拓展比B 教师的多,其原因在于A、B 两位教师的个人经验.

(2) 思想方法

中学数学中的思想方法分为化归、类比与归纳、方程的思想方法、函数的思想方法、数形结合的思想方法、算法化的思想共6 个.A 教师在教学中不仅渗透了上述的6 大思想方法,还讲授了许多的解题技巧方法,例如在求曲线的方程时有代入法、定义法、待定系数法等,求解过两点的椭圆标准方程时,一般方法是分别设焦点在x 轴上和y 轴上,快速高效的方法是利用待定系数法避免了分类讨论的情况,B 教师相对于A 教师使用的思想方法较少,如B 教师没有讲解待定系数法求解椭圆的标准方程.

2 研究结论

从三个维度分析了教师使用教材的情形得到影响教师使用教材的结论及因素有：

(1) 教师在进行教学时会根据学生在课堂上的表现以及课后作业的情况来调整对整个教材内容的课时规划,但这种调整并不大.教师在进行课时安排时会考虑到学生的基础,对于基础较差的班级,教师要花费更多的课时去进行习题的训练.

(2) 教材的课时安排会受到制度的影响(比如举行考试,教师需要加快教学的进度),有经验的教师愿意花费更多的课时讲授重难点,换句话,即有经验的教师对于教材的深度的挖掘比年轻教师更好,对于教材的本质有经验的教师把握得更好.

(3) 有经验的教师在进行课堂教学时能够将课标与教材、实际课堂联系起来,能够更好地培养学生的学科素养以及实践能力.

(4) 对于教材中的例题,探究与思考教师在进行教学时会将知识点提炼出来进行讲解,这样有利于引起学生的重视.除此之外,教师还会融入高考要考但是教材中并没有的知识点或者没有明确总结出来的知识点.

(5) 对于教材中的信息技术的使用,一线教师使用率低,有些教师基本不适用信息技术.

(6) 在知识点的深度和拓展上,教师在实际教学上的深度和难度比教材的大,且有经验的教师对于核心知识的把握比年轻教师的好.

(7) 在教材的忠实度上,年轻教师的忠实度大于有经验老师的忠实度.也就是年轻教师忠实于教材,有经验的教师对教材的改动比较大,在例题方面,改动的比较少,且有经验的教师改动大于年轻教师,但这种差距比较小.

(8) 对于练习题的忠实度,两位教师会根据学生的基础来选择练习题的难度,很少使用教材上的练习题.有经验的教师对于教材使用的忠实度低于年轻教师.

(9)年轻教师会对教学内容进行创新,但在创新的过程中要注意不能随意的创新,要符合实际.

影响因素：

1、教师个人因素

教师在进行教材的使用时会融入自己的教学方式,教师的教学经验的不同会影响到对知识点的拓展深度,教学经验越丰富,在使用教材时会考虑到学生的基础、高考的因素,经验丰富的教师在教学时, 往往可以以一个知识点进行拓展,比如一题多解、变式训练等.最后教师个人的专业发展也会影响教师对教材的使用.

2、学生因素

学生是教学的主体,教师根据学生在课堂上的反应和作业反馈来调整教学计划.学生的基础、对知识的掌握、作业反馈情况等都是教师在进行教材的使用时所考虑的因素.

3、制度因素

制度的因素影响着教材的使用,教材的使用顺序、教材的课时计划等,制度的因素分为高考和学校或上级部门制度两个层面,高考可以说是影响教师使用教材的最大因素,因为高中是为大学选拔人才,教材在使用教材时首先考虑的是知识的落实以及提升学生的解题能力,教师在进行教材使用时会根据高考的考点进行知识的迁移、拓展、变式训练等.

4、教材本身因素

教材的内容编排方式、设置和高考的对接也会影响着教师对教材的使用,对于高考来说,教材上的内容是远远不够的,深度和广度也不够,所以教师在使用教材时,会拓展知识点,讲授教材中没有的知识点.

3 研究思考

新一轮的课改正在进行,随着教育理念、目标的改变,教材不再是提供传授的材料,教师在使用教材时应该因材施教,考虑各方面的因素之后对教材进行深度挖掘.

1、教师应该不断的提升自我.年轻教师对教材的理解水平低,刚入职的年轻教师应该向有经验的老教师学习,教师是教学活动的主导者,学生是主体,在教学中教师是一个引导学生学习的角色,如果教师对教材意图理解不深,处理不好,甚至出现偏差,就会给学生带来误解 .再者要将教学与高考联系,不断地提升自己的专业知识,达到运筹帷幄,决胜千里的目标.

2、教师应树立正确的教材观.教师要仔细研究教材、课标、教学用书,理解每个问题背后的意图,教学是将教材中的知识结构转化为学生认知结构的过程,教师对教材要有整体的把握,从教材的整体入手,了解教材的编排意图,弄清每部分教材在整个教材体系中的地位和作用,用发展的眼光去处理教材.多思考编写者的意图,多问问几个为什么,经过一番思考,对教材的认识肯定会进一步提升.

3、将教材与实际生活联系,让学生体会数学是来源于生活,高于生活,应用于生活.

4、以学生为课程的主体.新课程提倡教师“用教材教,而不是教教材”,表现为在仔细分析学生的基础后,引导学生去学习新知识,使学生成为知识的最终拥有者.