深度融合信息技术的“正态分布”教学设计*

广东省广州市南海中学(510000) 丰梦婷

一、引言

“加强信息技术与数学教学融合的实践与研究”是全面深化数学课改的关键之一.融合的核心是要借助信息技术,为学生提供有挑战性的、互动交流的数学学习环境——保持应有的数学思考水平和强度,促进学生积极的思维参与.而作为点燃学生积极思维的导火线——提出和发现问题,理应成为贯穿教学设计的主线.因此,融合信息技术的教学设计,其要点在于：以问题引导学习,通过提出问题、独立思考、课堂讨论与交流、解决变式等多种活动,逐步深入、层层递进,最终解决问题并获得对数学知识的正确理解,并在“不知道怎么办”的问题场景中,萌生新思想,进而生成驾驭具体问题的数学方法[1].

二、融合信息技术于正态分布教学设计之原因探析

融合信息技术的教学设计,其特点在于充分、恰当地利用现代信息技术和信息资源,科学地安排教学过程的各个环节和要素,以实现教学过程的最优化.而如何做到“充分”和“恰当”,则需要教师明确融合信息技术的目的,制作、收集可以使用的信息技术课程资源,思考如何有效组织这些课程资源,明晰学生在融合信息技术的教学环境中对于数学知识的理解以及可能的误解.下文以人教A 版选修2-3“正态分布”为例,从以上几个方面展开分析.

(一) 融合信息技术的目的

明确融合信息技术的目的,即在教学中明确为什么要使用信息技术,它可以带来怎样的优势.在“正态分布”一节中,使用信息技术的目的之一：化抽象为具体,凸显数学对象的本质特征.例如为了引导学生认识正态曲线的本质特征——中间高,两边低,左右对称,首先借助信息技术展开高尔顿板实验,学生在增加试验次数的过程中,初步获得小球的分布情况——中间球槽内的小球比较多,两边球槽内的小球比较少.在此基础上,以球槽的编号为横坐标,以小球落入各个球槽内的频率值为纵坐标,学生借助EXCEL 绘制呈现小球分布规律的频率分布直方图和折线图,观察它们形状的共同特点.此时,再一次凸显了正态曲线的本质特征,给学生建立了正态曲线的直观印象.最后,借助几何画板演示当组距不断缩小时频率分布直方图的形状变化——越来越接近于一条光滑的曲线,并且具备“中间高、两边低、左右对称”的特点,第三次凸显了正态曲线的本质特征,与此同时,在组距不断缩小、不断逼近的过程中,也渗透了极限的思想.在此过程中,信息技术实现的三次凸显,让学生更容易把握正态曲线的本质特征.在本节内容中,使用信息技术的目的之二：化静态为动态,凸显数学对象之间的内在联系.例如在研究参数µ和σ 对正态曲线的影响时,借助几何画板的动态演示功能,学生可以直观感受到两个参数对正态曲线的影响.继而回归到正态分布密度函数中参数µ和σ 的位置以及本身的意义,那么,学生对于正态分布密度函数的由来也就不会感到突兀了.

(二) 可以使用的信息技术课程资源及组织形式

本节内容中,用于课堂教学的信息技术主要是几何画板和EXCEL.在新课引入时,使用了课程资源——高尔顿钉板实验演示程序(图1).在理解高尔顿板实验原理的基础上,学生动手操作高尔顿板实验, 在不断增加小球个数的过程中,观察演示程序中所呈现的小球的分布情况.

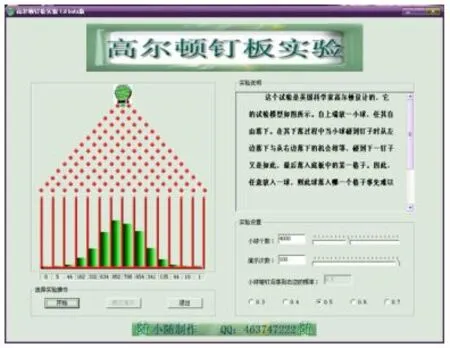
图1

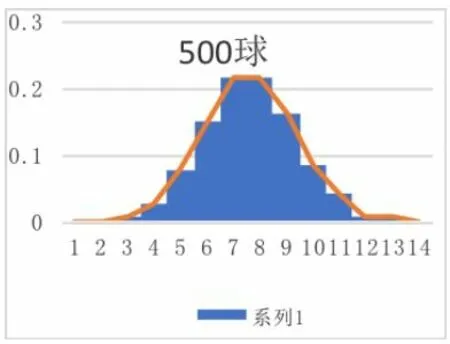
图2

在新课探究环节,以使用几何画板和EXCEL 制作的课程资源为主.在学生初步获得小球分布规律的基础上,尝试借助统计学中的图形工具呈现小球的分布规律.每个小组选择两组数据,借助EXCEL 制作频率分布直方图和折线图(图2).在探究正态曲线特点的过程中,学生动手操作几何画板,通过不断缩小组距,观察频率分布直方图的形状变化;通过改变参数,观察曲线的位置、形状变化(图3 和图4).

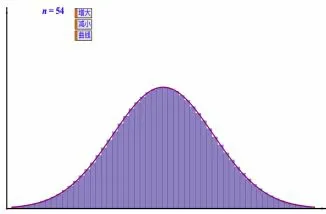
图3

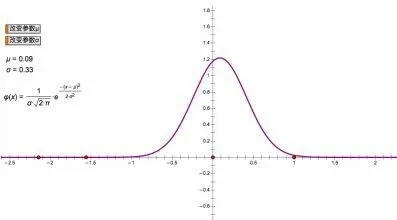
图4

(三) 学生在融合信息技术的教学环境中对于数学知识的理解以及可能产生的误解

通过动手操作高尔顿板实验——动手制作频率分布直方图和折线图——动手演示组距不断缩小时的频率分布直方图,有助于学生理解正态曲线的本质特征.因此,在探究正态曲线特点的过程中,学生对正态曲线的位置、对称性、峰值等特点脱口而出.几何画板在呈现正态曲线时,容易给学生带来误解,如正态曲线的两端是否会接触到x 轴,此时借助正态分布密度函数以及正态曲线的几何意义,可以有效化解学生的误解.

三、融合信息技术的正态分布教学设计

基于以上原因,笔者尝试将信息技术融合于正态分布教学设计中.

教学目标

1.借助历史上的高尔顿板试验,建立钟形曲线的直观印象——两头低,中间高,左右对称,从中渗透数学文化.

2.借助钟形曲线,引出正态分布密度函数解析式,引导学生结合解析式及概率的性质,借助数学几何画板,小组合作探究正态曲线的特点,揭示正态曲线的几何意义.

3.在理解正态分布定义的基础上,引导学生分析、认识生活中的正态分布现象.

教学重点

正态分布密度曲线的特点;正态分布密度曲线所表示的意义

教学难点

正态分布密度曲线所表示的几何意义

新课引入

解释高尔顿板试验原理

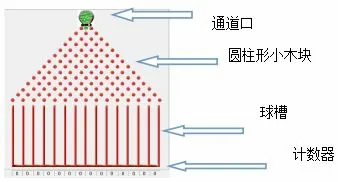
图5

著名的试验装置——高尔顿板试验装置.它的最上层是通道口,里面绿色的部分表示小球.中间层是圆柱形小木块,它们相互平行但相互错开,小木块之间留有适当的空隙作为通道.前面挡有玻璃.小球从通道口落下,与层层木块发生碰撞,每一次碰撞结果都有两种可能,一种是从木块左边的空隙落下,另一种是从木块右边的空隙落下,最后落入球槽中.最下面一行是计数器,它会统计出对应球槽内小球的个数.

新课探究

探究1高尔顿板试验中小球的分布规律

活动1：计算机演示高尔顿板试验

问题1：在投放小球之前,你能知道这个小球落在哪个球槽中吗?

问题2：随着试验次数的增加,落入球槽中的小球又将如何分布?

设计意图研究一个随机现象,就是要了解它所有可能出现的结果和每一个结果出现的概率.问题1 旨在让学生注意投放一个小球试验是随机试验,其结果就是球落在某一个小槽内.问题2 引导学生观察试验次数增加时小球的分布情况,思考高尔顿板试验中可能出现的结果.

问题3：能否借助图形工具来呈现球槽中小球的分布规律?

提示：从图形的角度,表示样本分布的方法有哪些? 如何建立坐标系?

设计意图由样本估计总体,一般分为两种,一种是用样本的频率分布估计总体的分布,另一种是用样本的数字特征估计总体的数字特征.从图形的角度,表示样本分布的方法有：频率分布直方图、频率分布折线图.引导学生回顾从图形的角度来表示样本分布的方法,探究小球的分布规律,体会样本估计总体的思想.

活动2：小组合作——借助EXCEL 绘图

以球槽的编号为横坐标,以小球落入各个球槽内的频率值为纵坐标.请各小组选择两组数据,截图到EXCEL 中,尝试运用EXCEL 绘制出频率分布直方图和频率分布折线图.

问题4：它们的形状有何共同特点?

设计意图通过学生自己动手操作完成频率分布直方图和频率分布折线图的绘制,引导学生对高尔顿板试验中的随机现象进行思考,建立钟形曲线的直观印象——两头低,中间高,左右对称,为建立正态曲线的概念设置铺垫.

探究2正态曲线的特点

问题5：如果不考虑小球的大小,不断缩小球槽的宽度,那么频率分布图的形状会发生怎样的变化?

越来越接近于一条光滑的曲线——总体密度曲线,它可以反映总体的分布情况.这条总体密度曲线具有两头低、中间高、左右对称的特点,我们说它像一条钟形曲线.我们把这种钟形曲线称为正态分布密度曲线,简称正态曲线.这条曲线所对应的解析式称为正态分布密度函数.这个函数中,有两个参数µ和σ,µ——均值,σ——标准差.

设计意图借助几何画板演示,让学生直观形象地感受频率分布直方图和折线图的极限形状,完成由离散型随机变量到连续性随机变量的过渡.从描述钟形曲线形状的角度引入正态曲线和正态分布密度函数的数学表达式.

活动3：小组合作——探究正态曲线的特点

问题6：结合正态分布密度函数和正态曲线,研究正态曲线的特点.

当µ和σ 确定时,这条正态曲线又有何特点? 当σ 一定时,µ的变化会对曲线产生什么影响? 当µ一定时,σ 的变化会对曲线产生什么影响?

设计意图借助几何画板直观感受两个参数对正态分布密度曲线的影响,进而得出正态分布的一些其他性质.通过小组合作交流的方式探究正态曲线的特点,突出本节课重点.

探究3正态分布

问题7：能否借助正态曲线准确计算出随机变量X 落在区间(a,b]内的概率?

提示：(1) 用频率估计概率;(2) 定积分的几何意义：平面图形的面积.

设计意图研究一个随机现象,就是要了解它所有可能出现的结果和每一个结果出现的概率.即不仅需要了解随机变量的分布规律,而且要了解它的概率分布规律.对于离散型随机变量而言,分布列完全刻画了它的概率分布规律,但是现在无法知道所构造的随机变量的分布列,所以只能通过频率来近似.

问题8：分析高尔顿板试验中,小球的分布为什么近似服从正态分布?

小组分享：一个随机变量如果是众多的,互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.

问题9：试分析某一地区同年龄人群的身高近似服从正态分布的原因.

设计意图正态分布广泛存在于自然现象、生产和生活实际之中,通过分析,旨在让学生学会发现生活中的正态分布现象.

归纳小结这节课,我收获了什么知识? 在正态曲线、正态分布概念的得出和正态曲线特点的探究上,我们收获了什么数学思想方法? 还有什么困惑?

教学反思运用信息技术使得数学对象直观化、动态化,可以帮助学生建立直观印象、理解数学对象,但是这种直观印象是表面的,教师不能仅仅停留在让学生看看数学对象的直观形式,还需引导学生从代数的角度分析产生这种特征的原因,由形回归到数,学生才能获得更深层次的理解.例如学生在观察正态曲线的动画演示后,容易得到正态曲线的一系列特点,但是为何会有这些特点? 教师要引导学生回归到正态分布密度函数上,对正态分布密度函数的本身特点进行分析.

四、结束语

融合信息技术的教学设计,需要教师明确融合信息技术的目的,制作、收集可以使用的信息技术课程资源,思考如何有效组织这些课程资源,明晰学生在融合信息技术的教学环境中对于数学知识的理解以及可能的误解.因此,如何做到充分而恰当的融合? 在融合信息技术之前,需要教师洞穿知识点所处的相关知识结构的环节,剖析学生发生这一知识点的心理环节,精心设计信息技术的呈现方式,如此,方能让信息技术在教学中最大限度地发挥功效.