加强课堂教学研究,培养学生核心素养—一道解析几何定点问题的课堂探究

广东省广东实验中学越秀学校(510095) 吴爱明

普通高中数学课程标准(2017年版)指出：“数学教育也承载着落实立德树人根本任务, 我们要提升学生的数学素养,促进学生思维能力、实践能力和创新意识的发展,探寻事物发展规律.”[1]数学学科核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析六个方面.如何在课堂教学中引导学生进行课堂探究,从而让学生实现数学学科核心素养的提升.我以一道解析几何定点问题的课堂探究活动为例,进行探究分析小结.在高二讲完解析几何后的一次周测中,老师命制了一道定点探究问题,作为初学解析几何的学生来讲,确实有一定的难度,做对的同学较少,但是,本题是解析几何中非常典型的一类问题,学生必须掌握并能融会贯通.虽然教学时间紧张,为了培养学生的核心素养,真正加强学生的分析解决问题的能力,我借助对这个题目讲评机会进行一次探究性课堂.现将课堂设计实录叙述如下.

一.原题呈现与解法探究

题目已知动圆C 过定点A(2,0),且与直线x = -2 相切.

(1) 求动圆圆心C 的轨迹方程;

(2) 若过点A(2,0) 的直线l 交第(1) 问所求曲线于P、Q 两点, 在x 轴上是否存在一点N, 使得对直线l 都有∠PNA = ∠QNA,若存在,求出点N 的坐标;若不存在,说明理由.

(引导学生分析解决问题思路)：

师：探究1动圆圆心C 满足什么曲线的定义?

生1：根据题意,满足抛物线的定义.

师：探究2像这样的动点轨迹问题用什么方法求方程?

生2：定义法.

然后,学生自己计算求出方程.

师：探究3第二问中的∠PNA = ∠QNA 可转化成什么关系? 用什么表示? (画出草图,进行引导),这是解题的突破口.

(师生共同分析)得出：可看成PN 和QN 的倾斜角互补.从而有kPN=-kQN,即kPN+kQN=0

解题过程：解：(1) 由抛物线定义知：动圆圆心的轨迹为以A(2,0)为焦点,直线x = -2 为准线的抛物线.设抛物线方程为y2= 2px.因为所以p = 4,所以动圆圆心的轨迹方程为y2=8x.

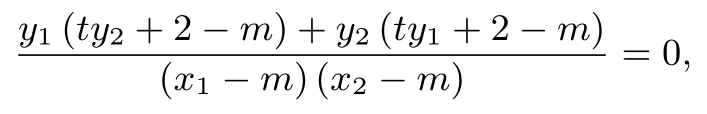
归纳分析：本题中的动直线刚好过抛物线的焦点,满足条件∠PNA=∠QNA 的点N 正好是抛物线准线与x 轴的交点.

这时,我并没有认为本题讲完就结束,而是继续引导学生进行探究,提出这样一个疑问：刚才这个分析结果是一种巧合,还是遵循他的一般规律?

探究4它对所有的抛物线都满足吗?

为此,我大胆提出猜想,给出抛物线中的一般结论：

二.抛物线中过焦点的弦一般结论

性质1已知抛物线y2=2px,过焦点的任意直线l,且与抛物线交于P,Q 两点,N 为抛物线准线与x 轴的交点,则∠PNF =∠QNF.

由学生仿照前面的方法进行证明如下：

证明直线l 的方程为则由得y2-2pty-p2=0.设P (x1,y1),Q(x2,y2),则y1+y2=2pt,y1·y2=-p2.因为

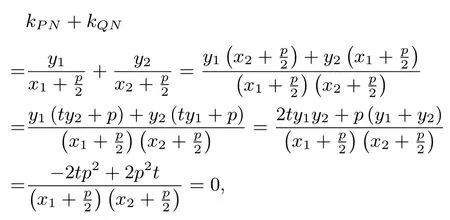
所以kPN=-kQN即∠PNF =∠QNF.

三.运用类比思想,在其它圆锥曲线中进行横向探究拓展

(乘热打铁)运用类比思想,进一步探究：既然在抛物线中满足这种关系,那么在其它圆锥曲线中是否成立?

先给出一个具体例子：

题目已知动点M 到定点F(-1,0)和定直线x = -4的距离之比为设动点M 的轨迹为曲线C.

(1) 曲线C 的方程;

(2) 过点F 作斜率不为0 的直线l 与曲线C 交于两点A,B, 定直线x = -4 与x 轴交点为P(-4,0), 设直线PA,PB 的斜率分别是k1,k2,求证∠APF =∠BPF.

(学生当场探究,当堂解答)

(2) 设直线 l′: x = ty - 1(t0), 则A(ty1-1,y1),B(ty2-1,y2).由联立得：(3t2+4)y2-6ty-9 = 0.因为所以即k1+k2=0,所以∠APF =∠BPF.

分析归纳根据圆锥曲线的统一定义可知：F(-1,0)为椭圆的焦点,定直线x=-4 是椭圆的准线,P(-4,0)即为椭圆的准线与x 轴的交点.也符合上面的结论.因此,给出以下两个性质：

性质2已知椭圆过焦点F(c,0)的任意直线l,且与椭圆交于P,Q 两点,为椭圆的准线与x 轴的交点,则∠PNF =∠QNF.

性质3已知双曲线过焦点F(c,0)的任意直线l,且与双曲线右支交于P,Q 两点,为双曲线的准线与x 轴的交点,则∠PNF =∠QNF.

(归纳出这两个性质后,下课铃响了.我将这两个性质让学生作为作业课后探究证明,第二天上课进行展示).

四.利用由特殊到一般思想,在圆锥曲线中进行横向探究拓展

探究5如果在圆锥曲线中,过的不是焦点而是一般的点,是否还有这样的结论? 如果存在满足条件的点,它们有何关系?

为了探究这个问题,我给出了2015年全国新课标卷I 第20 题,给大家探究：这题正好考查了这个问题.

题目在直角坐标系xOy 中,曲线C :与直线y =kx+a(a ＞0)交于M,N 两点.

(1) 当k =0 时,分别求C 在点M 和N 处的切线方程;

(2) y 轴上是否存在点P, 使得当k 变动时, 总有∠OPM =∠OPN? 说明理由.

分析探究本题的直线过非特殊定点A(0,a),要探究y轴上是否存在点P,满足条件.

解答过程：(1) 略;

五.归纳总结规律,得出一般结论

性质4已知抛物线y2= 2px, 过定点A(t,0) 的任意直线l, 且与抛物线交于P,Q 两点, 在x 轴上存在一点N(-t,0),使得∠PNA=∠QNA.

性质5已知椭圆过定点A(t,0) 的任意直线l, 且与椭圆交于P,Q 两点, 在x 轴上存在一点使得∠PNA=∠QNA.

证明直线 l 的方程为 x = my + t,则由得(b2m2+a2)y2+ 2b2ty +b2(t2-a2= 0.设P (x1,y1), Q(x2,y2), 则y1+ y2=所以

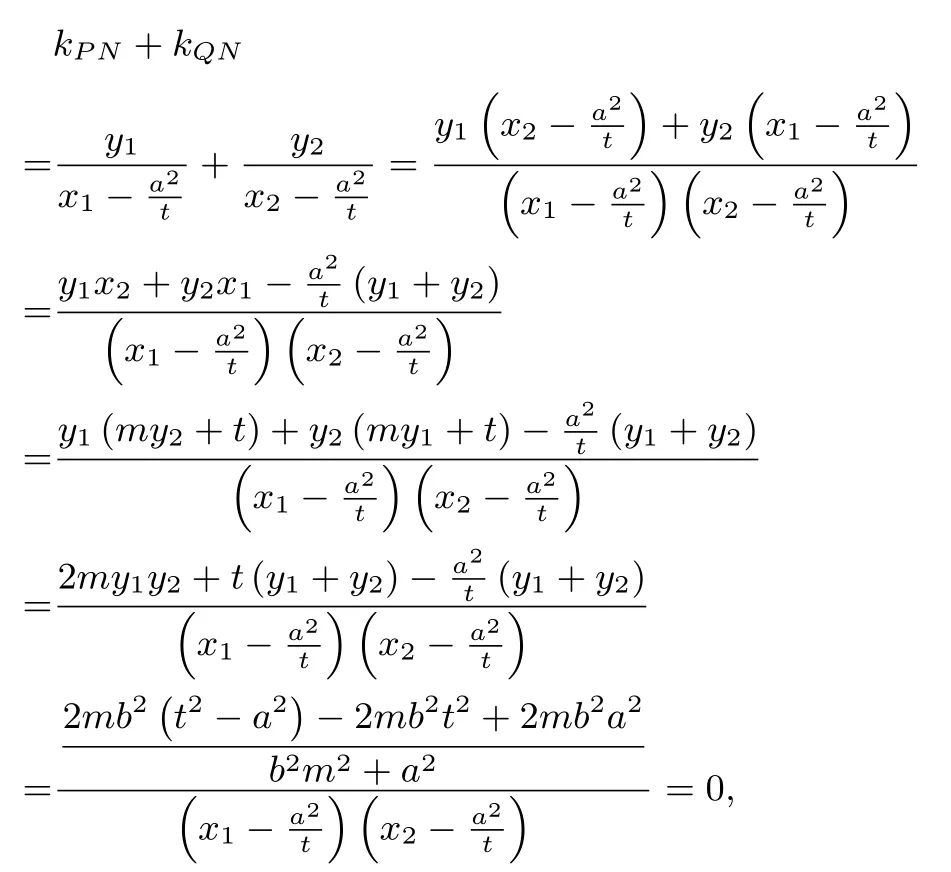
所以kPN=-kQN,即∠PNA=∠QNA.

性质6已知双曲线过定点A(t,0)的任意直线l,且与双曲线同一支交于P,Q 两点,在x 轴上存在一点使得∠PNA=∠QNA.

(性质4、6 供有兴趣的读者自己证明)

六.教学反思,总结评析

教学并不能为解题而解题,不要认为讲完一道题,学生就掌握了本知识和方法,而是要从不同角度审视问题.本次课就是基于核心素养视角下设计的.为了能够更好的培养学生的核心素养,教师在课堂教学中要有意识地引导学生进行“一题多解和一题多变”进行探究.通过独自或合作探究,逐渐养成一种问题探究的思维习惯,总之,学生能力是学生自己悟出来的,我们不能包办一切,只能正确引导.