从三维反向构建来初探高中学生思维的培养

四川省攀枝花市第七高级中学校(617005) 胡晓

如今现行的高中教育已经逐渐从应试教育中走向素质教育,在很多方面都取得了可喜的成果.从素质教育的出发点和落脚点来看是切实提高高中生的素质,因此应该首先明白什么样的素质是现阶段的高中生可以通过高中教育来获得和提高的(目标),其次才是怎样去有意地提高这样的素质(实践),最后是通过合理的评价体系来阶段性地检验是否达到应有的素质(评价).

解决第一个问题,我们应该去反思如今的社会最缺少什么样的能力和素质.从社会的发展趋势来看,如何能快速地获取和处理有效消息,并将处理的结果及时地应用于生活将成为一种必须的生存技能同时也是衡量人与人之间差别的重要指标.随之而来的是对于成功的定义也将趋于多元化.所以,在一定程度上,不管是学习还是工作可供选择的机会都大幅度地增加,与此相应的是选择的机会成本的增加.作为我们培养的毕业生,相比“千军万马过独木桥”的情形有了相当程度的缓解,但如何去进行有效地选择则变得非常重要了.笔者作为一线的高中教师,发现如今的高中生不存在学习能力上的问题,最大的问题恰恰是不知道如何选择.就数学学科而言,最常见的情况是不知道如何去“思考”问题.但笔者认为思考的方式和习惯本质上也是选择的结果.我们的教师很多是将教学的重点放在知识的传授和习题的训练上.不可否认,从短期的考试成绩上来看(笔者认为考试成绩只是评价学生的一方面而已)达到了预期的结果.但随着知识量的增加,这样的一种教学方式就凸显出其“桎梏”.最重要的原因是学生并没有将所学到的知识内化为自身的能力.当我们的学生遇到“相似”的问题时,不能很快地提取关键性的信息进行“连锁”的反应,(我们的大脑对于信息流的处理,首先是对信息进行有效筛选并提取; 其次是对信息进行编码;再次是对信息进行储存;最后如若信息重现,则可以提取编码信息并解码达到信息的联想和重现)因此他们对于习题的认识仅仅局限于题目本身的一种解题模式,做题很大程度上在于模仿.这当然也是一种很低水平的学习方式.要让学生改变这种被动的学习方式,真正学会如何去选择,提高思维的全面性和严谨性才是我们应该去反思的问题.

其次是第二个问题,解决的关键是应该把课堂重新还给学生.这同时衍生出另外一个问题——教师应该在整个教学过程中起到什么样的作用,扮演什么样的角色.笔者认为这里需要一个前提——学生已经具备了基本的知识储备和知识体系.即学生已经具备基本问题的解决的能力.那么能力的强化和提高则需要靠发现新问题和解决新问题来达到.这一问题实现的主要平台恰恰是最容易忽略的课堂.在平时的教学过程中我们可以尝试将知识体系与学生一起来搭建,与此同时注重知识的原始构成(original construction)和综合知识点的衔接.

最后一个问题,与第二个大问题有重合的部分,实践是检验真理的唯一标准.同样地,也只有通过实践才能有效地检验学生的学习能力.但这里的检验不仅仅是指普通的考试,更多地可以通过解决一些实际问题来检验.课堂内外都可以发现大量可以利用的素材.还有就是近些年来,设立“丘成桐中学数学奖”也是检验学生学习能力和动手能力的很好的途径.

下面我们通过三维的反向构建具体探讨其中涉及的一些细节.

立体几何作为高中数学的一个重要知识层面,对于学生空间思维的培养和逻辑推导能力的提升都起到了很好的作用.实践发现：通过三视图反向构建几何体是学生初学的一个难点.如何顺利地过度到立体几何的核心——边角面之间的度量关系,是高中数学教师首先应该面临的问题.在这里解决问题的关键在于对于“度量的不变性”的理解.

如果能顺利进行反向构建,首先必须明白三视图是几何体在三个不同视角下的投影.这里可以理解为用一个平面从三个不同的方向去截平面得到的最大截面图形.(本质上这也是一个三维转二维的问题,当然其反向构造就变成了二维转三维问题.) 其次才是如何利用二维图形的不变量来构造三维几何体.如果有必要,最后才是找出构造的几何体顶点的确定位置.

现在我们以长方体为例, 把三个二维图形得到的过程从一个统一的视角来观察.下图(图1) 是长方体ABCD-A1B1C1D1,其三视图(这里是从正面观察得到,因此侧视图和俯视图有一定的视角偏差,但对于整个长方体而言没有受影响.) 在其右侧.

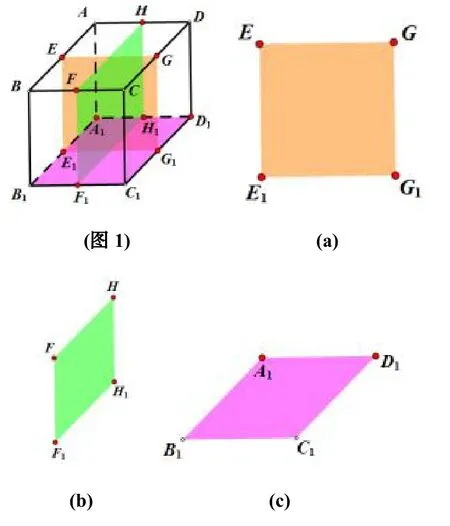
我们看到图(b)(c)看上去是平行四边形,这是视角问题,实际上两者和图(a)都是矩形.

又比如：(图2)是圆锥O-AB 及其在同一视角得到的三视图.

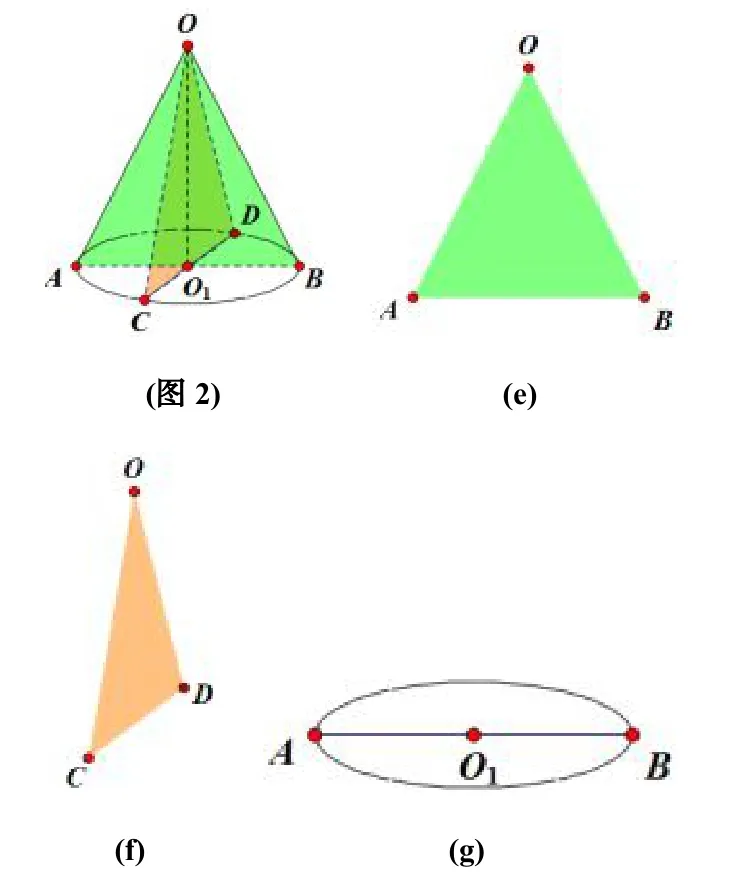
最后,我们以四面体A-BCD 来谈谈反向构建问题.与之前的两个例子类似,这里先假设得到了最终构建的四面体和其三视图.

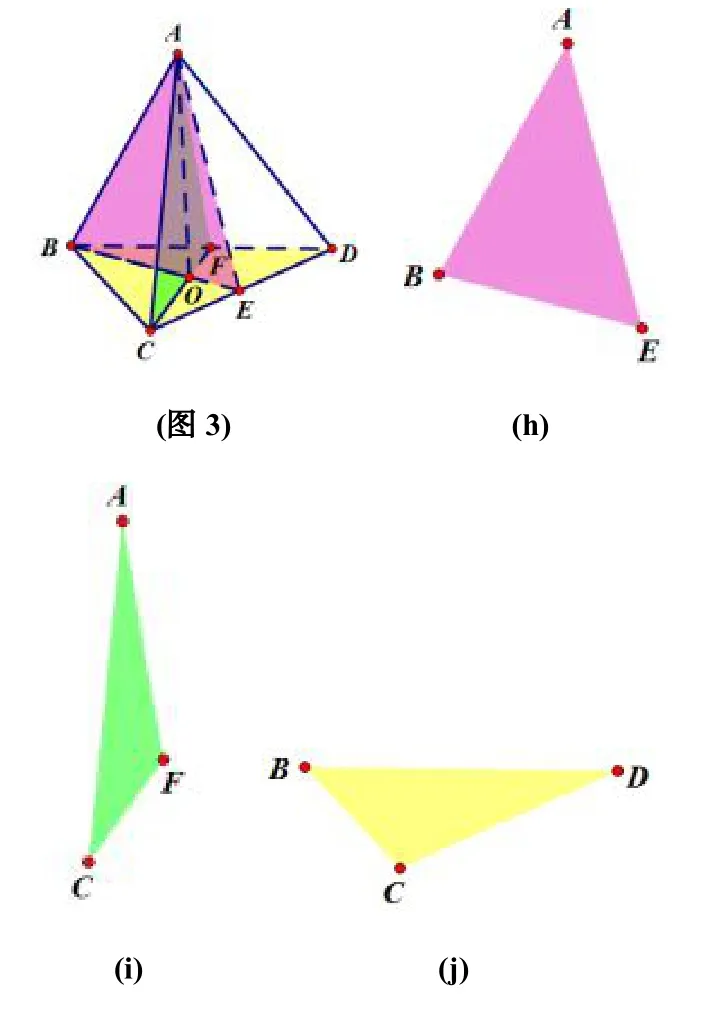
现在的问题是如何根据图(h)(i)(j)来构建(图3),需要说明的是我们看到的三视图还是由于视角的问题,与我们实际看到的有一定的偏差.为了更加符合对几何体的直观认识,这里从底面来构建几何体.具体的过程如下：

(1) 从三视图都是三角形可知,构建的是一个四面体;

(2) 由俯视图(j)可知：底面是△BCD;

(3) 正视图(h)和侧视图(i)所在平面相互垂直,且同时垂直于底面△BCD,则(h)(j)所在平面的交线必定垂直于底面(不妨假设垂足为O),即O 为A 在底面上的投影.这样就大致找到了顶点A 的位置;

(4) 连结AB,AC,AD 就构建出了四面体A-BCD.

注意在构建中应该抓住的“不变量”：

(1) 在俯视图中看到的就是几何体的底面,并没有发生任何变化;

(2) 在正视图和侧视图中,可以发现顶点到底面的距离.

下面以2014年四川高考理科数学的18 题再次加以说明.

例三棱锥A -BCD 及其侧视图、俯视图如图4 所示.设M,N分别为线段AD,AB 的中点,P 为线段BC 上的点,且MN ⊥NP.

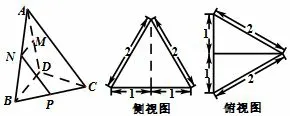
图4

(I) 证明：P 为线段BC 的中点;

(II) 求二面角A-NP -M 的余弦值.

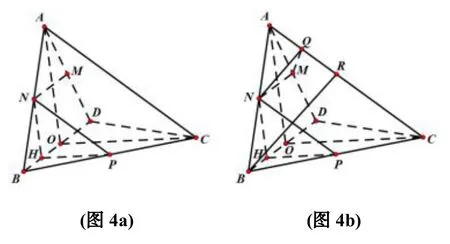
(I) 证明：如(图4a), 取BD 的中点O, 连结AO,CO.由侧视图和俯视图知, △ABD, △BCD 为正三角形因此,AO ⊥BD, OC ⊥BD.进一步可知, BD ⊥面AOC.又因为AC ⊂面AOC, 则BD ⊥AC.取BO 的中点H, 连结NH,PH.又M,N 分别为AD,AB 的中点, 所以NH//AO,MN//BD.又由AO ⊥BD,则NH ⊥BD.因为MN ⊥NP,所以NP ⊥BD.因为NH,NP ⊂面NHP,且NH ∩NP = N, 所以BD ⊥面NHP.又因为HP ⊂面NHP, 所以BD ⊥HP.又OC ⊥BD,HP,OC ⊂面BCD, 所以HP//OC.又因为H 为BO 的中点, 故P 为BC 的中点.

(II) 如(图4b), 作NQ ⊥AC 于点Q, 连结MQ.由(I) 知, NP//AC, 所以NQ ⊥ NP, 因为MN ⊥ NP,所以∠MNQ 为二面角A - NP - M 的一个平面角.由(I) 知, △ABD,△BCD 为边长为2 的正三角形, 所以由俯视图可知, AO ⊥面BCD.因为OC ⊂面BCD, 所以AO ⊥OC, 因此在等腰△AOC中,作BR ⊥ AC 于点R, 在△ABC 中,AB = BC, 所以又因为在面ABC 内, NQ ⊥AC, BR ⊥AC, 所以NQ//BR.又因为N 为AB 的中点, 所以Q 为AR 的中点, 因此,同理, 可得：所以在等腰△MNQ 中,cos ∠MNQ=故二面角A-NP -M 的余弦值为

评注在(I) 中能根据侧视图和俯视图快速识别△ABD,△BCD 是等边三角形是其中一个关键.在(II)中也可以建立空间直角坐标系来完成解答.

必须要承认上面这样的一个例子有一定的局限性.但对于学生思维的培养却是提供了一种可行性的方法.首先这是高中数学甚至大学数学中都会涉及到的反问题(inverse problem)的范畴.我们利用局部信息去推测或重构整体信息,问题的关键是找出两者信息的重合部分,即“不变量”.其次,学生对于这样的反问题的思考,很容易抓不住重点,本质上是没有统筹思考解决问题的意识.这就是经常容易见到的“只见树木不见森林”现象.由于数学内在的抽象性,最好这里用几何直观去让学生体验最终建构的目标和处理问题的源头.然后,就是建构顺序的选择.仅仅抓住“不变量”是解决问题的第一步,如何让建构的目标更加符合人们的普遍认识.从而让建构能够很顺利地进行下去才是解决问题的“转折点”.最后,通常意义下会用建构的目标去解决一些常规的问题(诸如：二面角、异面直线的距离等等).其实思维的培养其实就是建构过程.让学生主动参与到建构中去.不仅可以增强空间想象力和逻辑推理能力,更重要的是培育了学生问题解决的素养.对学生的后继学习都是非常有帮助的.