波利亚“怎样解题表”指导下的命题课教学

☉南京师范大学教师教育学院 葛雯琳

波利亚是美国著名的数学家和数学教育家，他对数学思维的研究具有划时代的意义，其中他提出的“怎样解题表”更是为中学数学教学提供了可操作性的指导.波利亚指出“中学数学教学的首要任务就是加强解题训练”，但是这里的“解题训练”并非是“题海战术”，而是问题的解决.他倡导的解题是一个探索的过程，是诱发学生思考和创造的过程.而“怎样解题表”实际上是一个用来培养学生数学思维的智力活动表.有研究者将波利亚的“怎样解题表”应用于中、高考题的解答，或是习题课的教学中，利用“怎样解题表”的操作顺序解决数学问题，让学生解一题，会一类.但是笔者认为不应局限于此，在数学命题、定理等的教学中亦可以渗透波利亚的“怎样解题表”思想.于是笔者结合之前的研究，设计出证明圆周角定理的教学片段，用实例说明如何在命题课中运用“怎样解题表”.主要通过大量的“解题提示语”来帮助学生完成新知识的形成过程.

一、波利亚“怎样解题表”的内涵

波利亚“怎样解题表”主要分为4部分内容：理解题目、拟定方案、执行方案和回顾.

遇到问题，第一步就是理解题意，目的在于对题目的整体分析，把握题目的条件和目标.在理解题目阶段，图形和符号与数学思维紧密相联，它们的使用有助于思考.因此，我们引入数学符号来表达一个文字提出的条件与结论.符号化的过程也是深入理解题意的过程.

在拟定方案的阶段，关键是找出已知条件和目标之间的联系，激发一个“好念头”的基础就是“过去的经验和已有的知识”.因此，“你以前见过它吗”是建立联系的第一步，但是有所遗憾的是，一般问题都与已有经验有所差异，因此，我们需要一些方法来对问题进行处理：对问题形式进行一定的转化，将一些专业术语转化为一般的语言分析.例如：“你能重新叙述这个问题吗？”用不同的方法去表述原题，使问题表述得更具有熟悉度，更简洁平易，更有希望解决.更甚，我们找不到已知条件和未知量之间的直接联系，那么可以考虑舍去一部分条件或结论得到相似的问题（特殊化、一般化），借助辅助问题的方法或结果来寻找思路.但我们对一个问题进行分解组合，有可能会在“变”中迷失，因此“回到定义上”作为不断提醒自己的有效提示语，让我们能时刻不忘问题之本.

表1

在执行方案的阶段，是零碎想法整体化的过程，是分析思路综合表达的过程.这需要我们做到对每个步骤的来源与作用了然于心.“你能看出来吗”“你能证明吗”，从直观上和形式上检查每一步骤的正确性，直观想象和逻辑推理并重而行.

在回顾阶段，对问题解决过程进行反思和推广应用，从而获得新的方法和经验.回顾本质上是从“理解性”和“发展性”两个方面来认识解题的过程.一方面，从理解的角度，回顾解题思路的发现过程，抓住解决问题的关键，总结解决问题的经验与教训.另一方面，从发展的角度重新认识问题，对问题的方法和结果进行推广深化，形成反思、评价的良好习惯.

解决一个问题给学生带来的喜悦感是培养学生数学兴趣的一大关键，而成功解决问题的路上并非一帆风顺，如果教师能够用这样激励性的“提示语”来帮助学生解答问题，让他们感受到“自然”，在这样的指引下，学生的独立思考能力一定会有所提升，对解决问题的方法也会有更深的领悟.从“解题”到“学解题”，是知识、技能到思想方法的升华.

二、在教学中善用波利亚“怎样解题表”

美国心理学家布鲁纳曾说过：“教学过程，是一种提出问题和解决问题的持续不断的活动.”波利亚的“怎样解题表”提供了一个清晰、完整的解题步骤，可以用于解决各式各类的数学问题.自然地，教学过程作为一个问题提出、求解的活动，“怎样解题表”在其中也有着重要的地位.“怎样解题表”含有大量的元认知提示语，这些提示语符合学生学习数学的心理特征规律，能够启发学生思考，将内在思维过程转化成显性的可操作性程序，对学生思维的发展有很大的促进作用.因此教师在教学中应善用“提示语”.

波利亚的提示语具有两个共同的特征：常识性和普遍性.因为常识性，所以学生自己也可能想出类似的问题，比较自然.因为普遍性，所以不直接指向结果，而是让学生有“事”可做，学生能够在自己的探索下进行活跃的思维活动，逐渐接近问题的中心，成功解决.如果教师经常使用这些“提示语”，并且学生在相同的“提示语”的帮助，反复几次，学生必然会注意到这些提示语进而尝试自己运用这些提示语，但凡有一次成功就能让学生对这些提示语有所领悟，从而逐渐理解、掌握、应用，形成自己的解题方法，归纳出自己的“提示语”.授之以“鱼”不如授之以“渔”，进而授之以“欲”.学生学到的远比具体的数学知识更加重要.

因此，在教学中教师若能将“怎样解题表”融于平时教学，善用“提示语”指导教学，必使学生的数学兴趣、数学思维有很大的提升.

三、圆周角定理教学片段

在引导学生猜想“圆周角的度数等于它所对弧的度数的一半”后进行验证，本设计意图如下：

让学生探索知识形成的过程，体会特殊化的转化思想和分类思想，掌握解决问题的一般规律，培养学生的创造、探索精神.

1.理解题意

用符号、图形语言表示出已知数、未知数、条件.

师：我们现在要验证猜想：圆周角的度数等于它所对弧的度数的一半.

师：题设是什么？

生：一个圆周角，它所对弧的度数.

师：结论是什么？

生：圆周角的度数是它所对弧度数的一半.

师：你能否画个图来解释这个猜想？

学生画出了一个圆周角∠BAC.

师：完整了吗？请你用你引入的符号来表述一下题设.

学生意识到题设中有两个量.

师：“它所对弧的度数”要怎么表示？回到定义上.

生：指弧所对圆心角的度数，（在图上画出了圆心角∠BOC）已知圆上一段弧BC，它的圆周角是∠BAC、圆心角是∠BOC，要证明：

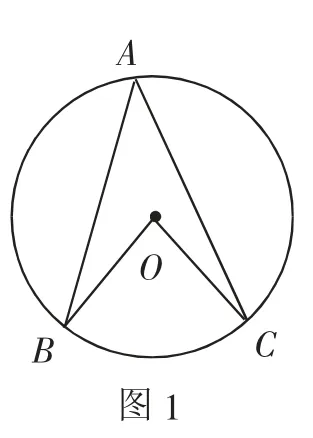
在老师的帮助下将问题用符号语言表述为：

已知B、C是圆上两点，A是圆上优弧BC上异于B、C的一点，证明：

设计意图：著名数学教育家斯托利亚尔曾说过：“数学教学也是数学语言的教学.”数学语言具体分为符号语言、文字语言和图表语言，简约而精准.将文字语言符号化、图形化是理解题意的关键，学生在“翻译”中抓住定理的关键要素，加深对问题的理解.

2.拟定计划——实施计划

师：你打算怎么证明？

生：这个∠BAC的位置我不确定.

师：很好，你意识到一个关键问题：点A是圆O上异于B、C的任意一点，这意味着有无数个圆周角.以前是否遇到过类似的问题？无限多个圆周角，是无数种情况吗？

师：我们之前是怎么解决无数多种情况的问题的？

生：取特殊.

师：无限多是不好研究的，我们可以化无限为有限，找到最特殊的位置关系，从最简单、最特殊的情况入手.

设计意图：圆周角定理证明的难点：无限种情况没有办法一一讨论，对于这样的情况，是否能借助以往的经验？由简入繁，通过一种简单情形的解决得到启示，进而解决复杂多样的情况，学生在证明定理中也学习到解决问题的一般思想方法：转化思想.

师：（几何画板展示点A运动）当点A运动的时候，观察∠BAC什么时候最特殊.

学生找到了最特殊的情况，如图3.

师：你能直接看出结论吗？

生：感觉像.

师：此时圆心O和圆周角∠BAC有着怎样的位置关系？

生：点O在∠BAC的边上.

师：现在，你对验证我们的猜想有计划了吗？

生：分情况：点O在∠BAC的边上和点O不在∠BAC的边上.第一个比较好证.

师：你先从简单的情况下手，这是一个很好的策略.那你打算如何证明点O在∠BAC的边上的情况呢？是否见过相同的问题？

生：三角形的一个外角等于与它不相邻的两个内角之和.

师：你想到了一个很有用的定理.你能利用它吗？

生：∠BOC=∠BAC+∠ABO，我不知道∠BAC和∠ABO的关系，它们看着像相等.如果它们相等，就可以了.

师：你看出了∠BAC=∠ABO，那你能否证明它们相等？你是否利用了所有的已知数据？有没有潜在的条件？

生：圆的性质！△ABO是一个等腰三角形，那就可以了.

设计意图：在解决问题的过程中，教师应引导学生充分调用以往学习的经验与知识，通过一些提示语“你之前见过这样的问题吗”，让学生感悟到数学知识、数学问题之间的联系，从而加深学生对问题的理解，也在无形中增加了学生的数学信心，将陌生的问题熟悉化.

师：根据你的思路实施你的证明.

证明略.

师：检验你的每一个步骤，你能否清楚地看出你的步骤是正确的？你能否证明这一步骤是正确的呢？

教师与学生检验证明过程.

设计意图：初中生正处于直觉思维与抽象思维的过渡期，教师应遵循学生的数学学习特点与心理发展规律，通过询问学生：“你能看出来吗”，培养学生的直观想象能力，在此基础上询问：“你能证明这个结论吗？”让学生体会到数学的严谨性，证明是检验想象的最佳途径，可培养学生的逻辑思维能力.

师：我们已经验证了点O在∠BAC的边上时结论成立.这道题解决了吗？

生：没，还有其他情形.点O在∠BAC的内部、外部时.

师：当点O落在∠BAC的内部时，你能证明结论吗？

师：这个问题与我们刚解决的问题相关吗？你能不能利用它？

生：应该能，但是这不是三角形，更别说等腰三角形了.

师：为了能利用它，你是否应该引入某些辅助元素？

学生提出：连接AO并延长，与圆O交于另一点G.

师：出于什么目的？

生：这样就出现了等腰三角形.

师：此时，你能证明吗？

学生实施证明过程.

师：通过添加辅助线，我们将点O落在∠BAC的内部转化成了点O落在∠BAC的边上的情形.

师：我们讨论了点O落在∠BAC上、点O落在∠BAC的内部的情况，还有点O落在∠BAC的外部的情形.这种情形我们该怎么证明？你能否利用之前的结果和方法？

生：按照之前方法，添加辅助线，连接AO，并延长与圆O交于另一点G，此时得到∠BOG=2∠BAG.

师：这与你要证明的结论有关吗？

生：只要∠COG=2∠CAG，相减就是我们要证的结论.

师：∠COG=2∠CAG是你猜想的还是你验证的？

生：我猜的，但是可以证明，就像证明第一种情况一样.

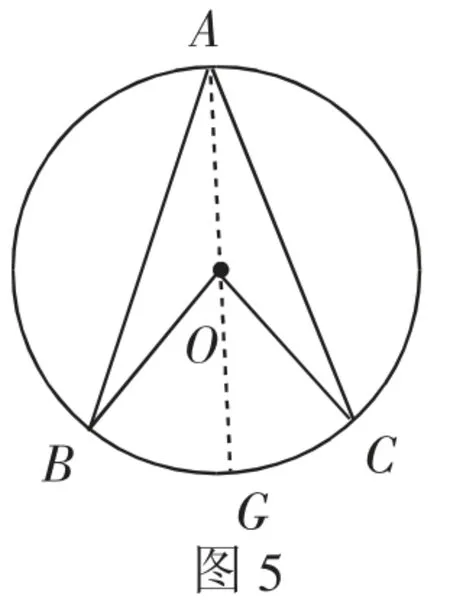
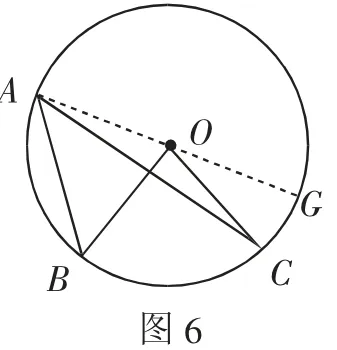
师：所以实际上，我们是把点O落在∠BAC的外部转化成点O落在∠BAC的边上的情形.给出你的具体证明.

证明略.

师：通过以上三种情况的讨论，我们发现：圆周角的度数等于它所对弧上的圆心角度数的一半，那么自然地，同弧所对的圆周角相等.

设计意图：教师通过“提示语”引导学生借助以往知识和经验去联想、去转化，往往需要一些辅助元素，将原题变换一下，增加问题的“相似度”，但是要提醒“要证明的是什么”，在变化中不要忘了原来的问题是什么.在这个过程中，学生充分利用脑中的知识网络，重组改造，一步步解决问题.

3.回顾

（1）反思总结.

回顾我们验证猜想的整个过程，同学们有什么感想？你能回答出以下问题吗？

①当我们遇到不熟悉的问题时，我们是怎么做的？

想想之前有没有遇到过类似的问题，借助已有的经验去解决问题.

②当我们遇到无限多种情况无法一一讨论时，我们采用什么样的方法？

寻找特殊的情况，将无限多个圆周角转化成三类有限的情况去讨论.

③采取这种方法的依据是什么？

依据点O与圆心角∠BOC的关系，通过有限的分类验证了无限的问题.

④在解决第二类和第三类问题时，我们添加了辅助线，这一做法出于什么样的目的？

利用已有的结果和方法，将第二类和第三类情形转化成第一类情形.

（2）推广深化.

你能不能把这个结果或方法用于其他的问题？

设计意图：回顾小结是提升学生能力的重要阶段，不仅是强调这节的重点、难点，更是从更高的角度审思这部分内容，将数学思想方法外显化，进行归纳、提炼，形成解决问题的一般方法，让学生有更多的收获.

四、结语

波利亚说：“只要应用得当，如果你向自己提出表中的这些问题与建议，可以帮助解决你的问题；而如果你向你的学生提出同样的问题与建议，你就可以帮助解决他们的问题.”平时教师若能有意识地将“怎样解题表”的思想渗透于命题课教学，不仅可以帮助学生解决现行的问题，还能启发学生运用这些“提示语”和方法自我帮助，培养学生独立解决问题的能力.在应用“怎样解题表”时，要注意根据学生反应灵活使用，上述操作并非死板的顺序.