让数学概念教学“慢”下来——记一次“多边形”的听课、评课与再设计

☉江苏省常熟市实验中学 季叶红

教研组的观课研究是各校开展的一项常规教研活动，但有些学校因为种种原因，听课、评课流于形式，开课质量不高、评课也是“无话则短”，匆匆收场，让参与观课、研究的老师感到这种教研活动的“无趣”，对于参与其中的青年教师来说，更加没有得到应有的专业提升.笔者最近参与一次校级听、评课活动，课后除了一些空话、赞歌式的点评，也听到一些有质量的商榷性建议，本文记录这次教研活动，并在活动之后继续开展教学研究.下面整理这次教研活动的一些听课手记、评课观点及教学再设计，供分享和研讨.

一、八年级“多边形”听课手记

说明：这是八年级上学期一节新授课，学生之前刚刚学过三角形的内角和、外角性质，教师引导学生类比三角形的概念归纳出多边形的定义及相关概念（边、角、对角线），接下来是研究多边形的内角和性质.

教学片段（一）多边形内角和性质的教学

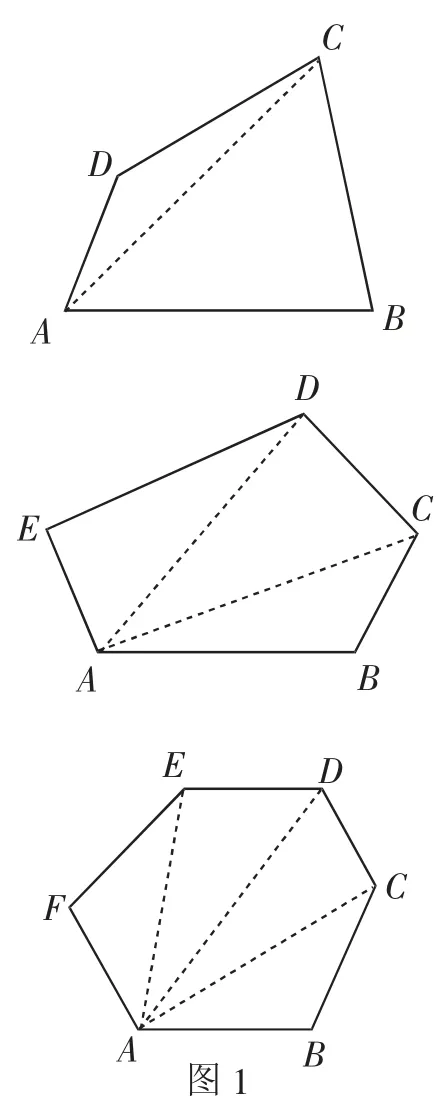
师：同学们复习一下三角形内角和，再观察图1中的三个图形：

课堂观察：学生在老师的“引导”之下，很多对图1中三个图形（四边形、五边形、六边形）内角和都顺利解决，并总结出多边形内角和与三角形内角和的关系，从而归纳出多边形内角和公式.教学进程推进非常高效，学生似乎也学得很有兴趣.

接着，教师安排三道练习题，检测学生对于多边形内角和公式的理解及应用情况.

对于直接应用的题目，大部分学生能够熟练应用公式解决，但是对于稍有变化的题目，部分学生不能灵活变通，无法独立解决.

教学片段（二）一道练习的学生讲评

例题：如图2，求∠A+∠B+∠C+∠D+∠E+∠F的度数.

教学观察：这一环节用去近10分钟，学生纷纷积极参与（上台讲解不同解法的学生多达5人次），很多学生愿意把自己的方法分享给其他同学，学生共同合作学习.不少“学困生”参与的热情十分高涨，学生自主学习的热情很高.

二、评课意见摘要

课后，参与听课的老师进行了评课，多数评课意见是贴标签式、唱赞歌式的“说好话”“空泛之谈”，也有一些商榷意见，以下是几种典型建议或观点.

观点1：探究多边形内角和性质时，可以放手让学生用不同方法探究，而不是设计好流水线式问题，禁锢学生思维活跃的空间.这里可否引导学生尝试多角度分割三角形？平面上只需再找一个点，就可以与多边形的顶点构成三角形.这个教学环节体现了从特殊到一般的研究方法，让学生找出从一个顶点引出对角线条数、分成三角形的个数、内角和与边数的规律.但是本课教学时直接就给出了探究多边形内角和的方法，即分成三角形，固化了学生的思维.学生在小学时对多边形内角和已经有了一点了解，所以在初中阶段应该更加强调更高层次的证明.想起自己在这个内容教学时的一些经验，在教学中可以发现，学生能想到的研究内角和的方法还是比较多的，比如，有的学生将五边形分成了一个四边形和一个三角形，有的学生想要用度量的方法等.这时指出学生所提出的研究方法的利弊之处，更有利于学生发散思维的形成和对内角和证明方法的理解.

观点2：在研究了多边形内角和之后可否追问：同学们还想研究多边形的什么性质？由内而外学生会自然由上一课时给出的外角定义提出研究多边形的外角和.这时候让学生大胆猜测，然后小心求证，放手让学生探究.

观点3：这是一种典型的应试教学下的习题课教学，属于应该抛弃的“一个定义，三项注意，大量练习”（章建跃语）教学方式.从定理教学或概念教学来看，应该注意概念、定义的生成、归纳与证明，让学生感受数学的逻辑、理性精神，即理解“客从何处来”.

观点4：这节课的备课要注意查阅、研习“教参”旁白、脚注上大量的说明，如类比、推广、特殊到一般、从简单出发、化未知为已知等，这些都是具体细节处理时的立意.

三、多边形教学重点、难点与教学建议

多边形的教学值得研究和推敲，因为一节课容量有限，学生需要学习什么，教师该把什么教给学生，把重点环节放在哪里，这些都非常关键.

1.明辨多边形的教学重点与难点

多边形是接续在三角形之后学习的，所以它的生长点在三角形.比如，三角形是按图形定义、三角形要素（边与角的关系）、三角形相关要素（如三角形中的重要线段，三角形外角，三角形的周长与面积等）展开学习的，这是研究一个新图形的基本套路.我们完全可以类比三角形学习的方法和重点，想清多边形的教学重点也应该是多边形的定义、多边形要素之间关系、多边形相关要素之间的关系，并在这样的路径下渐次生长、丰富知识结构，而不是快速推进，搞“一个定义、三项注意、大量习题”的教学方式，虽然上文记录的习题教学片段也有学生精彩的表现，但那是多边形后续习题课教学时可以有的课堂表现，不应该成为多边形新授课的教学重点.

多边形教学的难点则在新元素——对角线的介入，会引发很多新的功能或性质，比如，在探究多边形内角和性质时，对角线就起到很大的作用，成为有效转化的重要工具；而多边形对角线还涉及如何“有序”计数的方法渗透，这些都是多边形教学中的难点，处理得当，不但可让学生对与对角线有关的知识有较深的理解，还能通过研究一个新的几何对象的相关要素，使学生学会研究方法，并向学生传递“成果扩大”的研究取向.

2.多边形的学程导进与操作建议

对于本节课，我们为什么要研究多边形的内角和与外角和？教师可以引导学生类比已学的三角形相关知识去思考这一部分的知识框架，从而明确学习目标.因此，第一个环节可以围绕我们已经学过三角形的哪些相关知识（定义、边、角、“三线等”），思考对于多边形我们已经掌握了什么（定义、对角线、正多边形等），还可以研究什么.这种对于知识体系的整体把握能够培养学生自主学习、探索的能力，对学生来说将是受益无穷的.

接下来，可以引导学生寻求一种方法归纳出多边形的内角和公式，作为工具方便使用.这个环节不可操之过急，问题的设计也应该更具开放性.

因此，如图3，有三个图形，不添加对角线，学生小组进行合作探究，看能否探讨出方法.如果学生没有思路，可以提示学生思考四边形与三角形的关系，引导学生通过分割的方法求出四边形的内角和，请一组学生展示完整探究过程，再请其他小组同学类比此方法，探究并归纳出多边形内角和的一般计算公式.

在学习得出四边形内角和之后，可以跟进提问：如果四边形的一组对角互补，那么另一组对角有什么大小关系呢？你能证明吗？通过刚才的探究过程，学生对于这个问题大致有两种思路，第一种是延续前面的方法，连接对角线进行分割；第二种方法是直接应用多边形内角和公式.一方面，学生会加深对复杂图形进行分割研究的方法的理解；另一方面，可以加强学生对本节课重点知识的熟练掌握及应用.

课堂小结时，安排总结这节课我们是如何研究多边形的，学到了什么内容，又学到了哪些方法，对于多边形后续还可以研究什么问题，这样的数学教学，不光是知识的传递，也应该是方法或套路的传递.