开拓学生数形结合的数学思想——以二次函数的图像为案例

☉浙江省桐庐县实验初级中学 周建洪

初三学生已经有了一定的数学基础，但是数学思想的构建仍然是一大难点.回忆自己的中学阶段，数学教材分为《代数》、《几何》、《三角函数》，当时的学习情境历历在目，各部分内容都是孤立的体系，教师也很少“灌输”数学思想，试题的知识点也是无渗透的.现如今笔者成为一名教育工作者，对教数学有了深刻的理解：教给学生的是数学的思想方法，是数学的核心素养.

一、对数、形的理解是课堂教学的前提条件

近来授课的内容是“二次函数的图像”，是学习过二次函数的概念之后的一节内容，知识内容就是代数向几何的渗透，是数形结合思想的真实展现.作为这节课的集体备课中心发言人，笔者有着渲染“数学思想”义不容辞的责任.在研究过程中笔者提出了三个观点：

第一，二次函数是一种自变量与函数对应的关系，按照教材的设计，可以让学生在课堂上完成最简单的二次函数y=x2，在x的取值范围内列出函数对应值表：

表1

第二，让学生建立直角坐标系（准备好坐标纸），在直角坐标系中将相应的点标出来，然后用光滑的曲线连接起来.将数标成对应的点，绘成二次函数图像，这正是数形结合思想，在课堂教学中对初中生传递这样的思想，有利于他们数学的能力发展和素质的提升.

第三，引导学生认识二次函数的图像的具体特点，引出抛物线的概念、抛物线的顶点的概念和抛物线开口的方向等.在课堂上，必须让学生熟练掌握二次函数的图像的具体特点，预设具有针对性的课堂填空练习.通过抛物线的基本特征让学生由形转化为数，明确抛物线上的任一点如顶点等都是满足二次函数表达式的，也就是说，在抛物线图像上取两个点代入二次函数的一般表达式，就可以得出函数表达式.学生经过反复敲打锤炼，数学思想就会潜移默化，就会成为素质.

笔者的建议很快得到了学科组教师的认为.大家一致认为，从“数”出发，拓展到“形”，是一种无形成为有形的过程；从“形”出发，回归到“数”，是一种有形成为无形的过程，这都是数学最基本的思想方法.形成数形转换的思想方法是学习的难点，如果在这方面有所缺失，学生的数学基础知识就是一些孤立的碎片，就无法完善他们数学思维的学科素养.

二、创设数形转换的情境是拓展课堂教学的引燃剂

如何在“二次函数的图像”教学过程中引出数形结合的思想呢？笔者提出了自己的看法.在课堂上创设一个将二次函数与图像紧密结合在一起的生活实际问题情境，从抽象的函数式转换为直观的图像，从而激发学生的学习兴趣，为课堂的学习探究奠定扎实的知识基础.

在集体备课组讨论课堂情境创设这一点上，有的教师认为开门见山是司空见惯的一种做法，可以不创设；有的教师则认为先复习二次函数概念，再导入新课；也有教师和笔者同感，认为情境创设是一种组织课堂教学的形式，是引导学生在课堂上对知识进行探究拓展的出发点，是厚积薄发.如介绍大多数桥梁是根据二次函数的图像设计的，在课堂上展示一些桥梁图片，如图1.

图1

学生一定会提出质疑，为什么说这些桥梁与二次函数的图像有关系呢？二次函数的图像又是怎样的图像呢？及时疏导尤为重要.可以让学生自主作出二次函数y=x2与y=-x2的图像.

第一步引导是列表：在x的取值范围内列出函数对应值表：

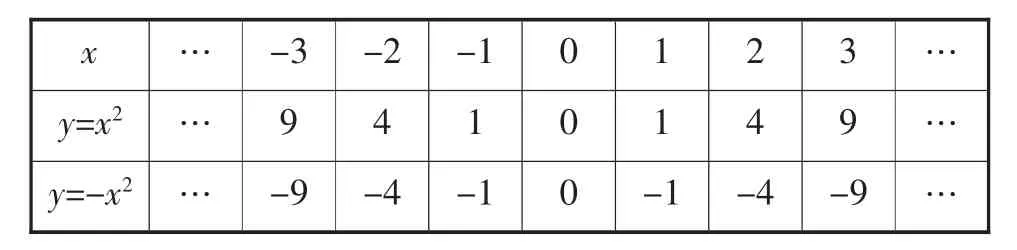
表2

第二步引导是描点、连线、作图，结果如图2.

尽管初中生已经对数从有理数、无理数等方面进行了认识，但对数与形的认识还是很肤浅的，如果在学习二次函数图像时教师用心引导，在导入新课之前创设让学生明确、吸纳并能够运用数形结合思想方法的情境，在课堂探究二次函数图像的过程中运用数形结合思想的步骤、解题方法等，何尝不是激发学生对数学的知识探究产生兴趣的一种有效途径呢？

图2

三、动手实践，让课堂成为学生勤于思考的主战场

在设计课堂例题时，笔者提出以教材例题为线，但例题必须是学生动手、动脑的结果，学科组成员一致同意这个意见.但如何引导学生动手、动脑，是独立思考还是合作探究，则出现分歧.

教材中的例题1：已知二次函数y=ax2（a≠0）的图像经过点（-2，-3）.

（1）求a的值，并写出这个二次函数的表达式；

（2）说出这个二次函数图像的顶点坐标、对称轴、开口方向和图像位置.

在集体备课的研讨过程中，笔者对教材例题进行了细致分析：题干给出的y=ax2（a≠0）是简单二次函数的一般表达式，而图像经过点（-2，-3）体现的是形对应数的思想，这正是例题第（1）问要解决的问题；而第（2）问“说出这个二次函数图像的顶点坐标、对称轴、开口方向和图像位置”则是由数转形的思想.因此，例题有着代表性和实用性.

为了让学生明确二次函数图像在生活实际中的应用，还建议预设抢答的形式处理一些课堂问题，看看如下案例：

某建筑工程师在1000米的河道上设计了一座拱桥，其高为15米，设计图纸如图3：

图3

（1）拱桥的下沿是什么形状？怎样建立坐标系？

（2）这条曲线的一般表达式是什么？

（3）你认为该曲线经过了什么点？

（4）写出该曲线的函数式.

设计这类练习的目的在于对例题进行变式和拓展，学生在例题的基础上进行抢答，既渲染了课堂气氛，解决了初中生由于课堂时间过长而引起的倦怠，同时巩固了学生所学新知，体验了数形转换思想在生活实际中的应用.

有的教师提出，学生动手还可以采用教材中的课内练习，这当然是可以实施的.但笔者认为，教材的课内练习与生活实际还是有差距的，学生的练习仿佛纯理论的东西，不利于学生开阔视野，结合生活实际才能让学生更感兴趣，有决心去挑战自己的极限，用数学的眼光看世界.在各抒己见的集体备课活动中，有争议是难免的.教材编写专家自有道理，而让学生的激情迸发出来是教师应具有的专业素养，是教师驾驭课堂的能力.这一环节的设计还是因人而异吧，不再评价各位教师预设的好坏，还是让课堂实践给出证明吧.

还有一个课后环节需要简单地说明一下，那就是课后练习，是课堂知识的延伸，教材习题就很不错，也可以补充两道近年来的中考试题.

总之，这次集体备课给了笔者一个中心发言的机会，也可以说是因此再提升教育教学能力的机会.没有过程的辨析，就没有教学经验的升华.笔者在集体备课时也只不过将数形结合思想娓娓道来，而初中数学知识体系中的数学方法和数学思想如繁星满天.数形结合思想是学生在二次函数图像问题中解题的基本点，唯有教师在课堂上灵活地“灌输”数形结合思想，才能激发出学生数学思维的潜能，才能帮助学生开拓数学领域知识素养.