例说添加辅助线的方法——一道初中几何题的解法探究

☉湖北省秭归县归州镇初级中学 向晓琳

在初中数学的学习过程中，尤其是遇到稍难的几何题时，学生往往不知从何处下手，胡乱添加辅助线，反而使图形越来越复杂，思维更加堵塞，渐渐地对几何题敬而远之.其实，添加辅助线是根据题型来添加，根据条件的特殊性来添加，有时二者可兼顾.下面就具体例子来说明.

一、典例呈现

如图，在矩形ABCD中，AB=3，AD=6，点E是边AD的中点，一个含45°角的三角板EFG的直角顶点与点E重合，并绕着点E旋转.EF交BC于点I，EG交DC于点H.

（1）如图1，A、B、F三点在同一直线上.

①若DH=2，求BF的长；

②连接CG，求证：∠HCG=90°.

（2）如图2，FG经过点C，若CG=2，求EF的长.

二、解法探究：

（1）①法1：利用三角函数.

设BF=x，则AF=3+x.

由点E是边AD的中点，得AE=DE=3.

由∠AFE=90°-∠AEF，∠DEH=90°-∠AEF，得∠AFE=∠DEH.

则tan∠AFE=tan∠DEH.

法2：利用相似.

设BF=x，则AF=3+x.

由点E是边AD的中点，得AE=DE=3.

由∠AFE=90°-∠AEF，∠DEH=90°-∠AEF，得∠AFE=∠DEH.又∠A=∠D，则△AFE△DEH.

②法1：补成K型图.

如图3，过点G作GM⊥AD，GM交AD的延长线于点M.

易得∠AFE=∠MEG，∠A=∠M，FE=EG，则△AFE△MEG.则AE=MG=3=CD.

由∠ADC=∠M=90°，得DC∥MG.

则四边形DCGM是平行四边形.又∠M=90°，则四边形DCGM是矩形.

则∠HCG=90°.

法2：构造全等三角形.

如图4，连接BE、CE.

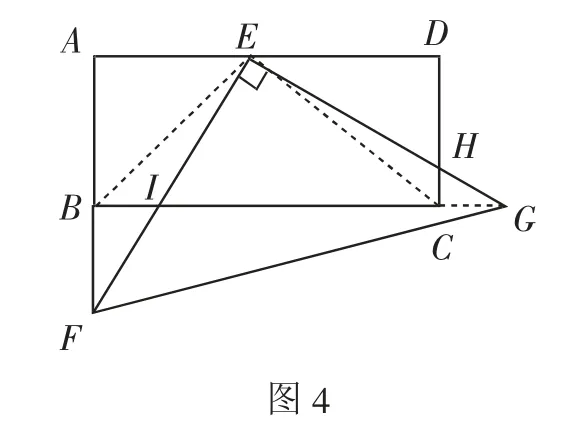
易知△ABE和△DCE是两个全等的等腰直角三角形.

则BE=CE，且∠AEB=∠DEC=45°，则∠BEC=90°.则∠BEF+∠CEF=90°.又∠GEC+∠CEF=90°，则∠BEF=∠GEC.

在△FBE和△CEG中，BE=CE，∠BEF=∠GEC，EF=EG，则△FBE△GCE.

则∠ECG=∠EBF=135°.而∠ECH=45°，则∠HCG=90°.

法3：证明三角形相似.

易得∠AFE=∠DEH，则sin∠AFE=sin∠DEH.

（2）法1：如图5，连接EC，过点C作CQ⊥EG于点Q.

则△CQG是等腰直角三角形.

法2：如图6，连接CE，过点E作EP⊥FG于点P.

则△EFP和△EGP是两个全等的等腰直角三角形.

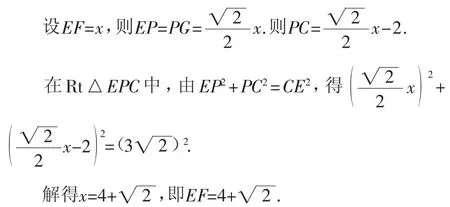
在几何问题中，辅助线的添加对学生来说并不陌生，在解几何题时经常用到.若几何图形中的某些量之间的位置关系或数量关系比较隐蔽，为了沟通相关量之间的联系，我们常常要在原图形中添加辅助线.这样可以化难为易、化隐为显.但添加辅助线，要因题而异，虽然变化万千，而且没有一个通法可遵循，但一般都能找到一定的规律和常用的方法.只要我们知道添加辅助线的目的，在图形中构造我们学过的基本模型，然后和模型的特征去比较，就可以利用它们的性质去创造有利的条件，从而使问题得到顺利解决.要想熟练掌握添加辅助线的技巧，必须对基本图形的性质十分熟悉，多动手、动脑，善于联想，横向、纵向思维要齐头并进.

总之，一道几何题所考查的知识点特别多，它不仅涉及学生所掌握的数学基础知识、所具有的数学思想和方法，还涉及学生的解题能力，所以教师应该加强解题思维的分析和学习方法的教学，努力提高学生解决问题的能力.