慧手作图 智取关联

（浙江省嘉兴市南湖区教育研究培训中心）

众所周知，很多代数或几何问题的解决依赖于作图.良好的作图能力可以启发解题思路，为解决问题提供很大帮助.经常动手作图，可以帮助学生更好地理解图形的基本性质和位置关系，建立几何直观，展开关联想象，从而把复杂的数学问题变得简明、形象，这有助于探索解决问题的思路，进而拉近题目条件与待求结论之间的距离，使得问题的解决事半功倍.笔者现结合几个实例来阐述几何作图在数学解题中的妙用.

一、作网格，以“图”的直观探寻方法

作图可以理解为一种从无到有的创造，它有助于提炼问题中的数量关系，并且进行直观表达，从而帮助学生分析问题和解决问题.例如，解答某些三角函数问题时，若能将构造的直角三角形放置在正方形网格中，则题目中的一些数量关系和关联结构就会自然显现，让问题的解答变得简单，甚至是一击而中.

例1已知,求α+β的度数.

解析：如图1，先作出正方形网格，然后根据已知条件，在正方形网格中作出∠ABC=α,∠DBC=β,于是∠ABD=α+β.借助几何直观和经验，不难观察并猜想∠ABD=45°,接着想办法证明∠ABD=45°.而要证明∠ABD=45°,只需要连接AD，证明△ABD是等腰直角三角形即可.

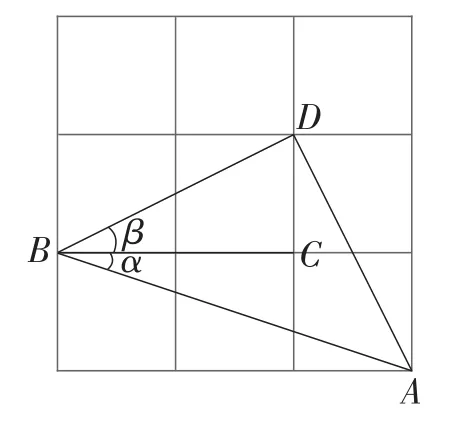
图1

此题中，在正方形网格背景中作出满足要求的角α和β，并将这两个角合并在一起，不仅能很快地判断出α+β=45°,而且不需要经历复杂的运算，只需要调用直观经验，借助简单的几何推理，即可找到答案，凸显了“寓数于形，以形解数”的应用价值.

二、作轨迹，用“图”的规律启发思维

初中阶段，许多“求最值”的问题都与点的轨迹有关.求解此类问题时，若能作出动点或动线的轨迹，并通过作图形去思考和发现规律，那么问题就会迎刃而解.

例2如图2，在边长为1的正方形ABCD中，将射线AC绕点A按顺时针方向旋转α度（0°＜α≤ 360°），得到射线AE，点M是点D关于射线AE的对称点，则线段CM长度的最小值为（ ）.

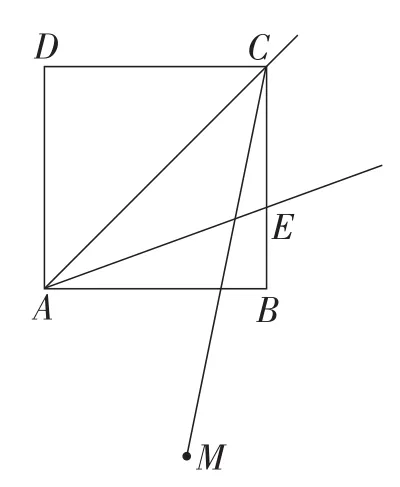
图2

解析：如图3，先作出射线AE在不同位置时，点D关于射线AE的对称点M（例如，当射线AE与直线AC重合时，点D关于射线AE的对称点为点B；当射线AE与直线AB重合时，点D关于射线AE的对称点为点M1），然后观察这些对称点的位置特征，再通过直观想象与操作验证，不难发现这些对称点在以点A为圆心，AB为半径的圆上，即点M的轨迹是以点A为圆心，AB为半径的圆，进而得出当点M在正方形对角线AC上时，线段CM长度的最短，最小值为

图3

此题要求动线段CM长的最小值，解答时很难直接想到解题思路.即使有学生想到利用三角形的三边关系去解答，并且连接了AM，知道了CM≥AC-AM，也不一定能想到线段AM的长是定值1.更何况利用三角形的三边关系推出CM＞AC-AM容易，推出CM≥AC-AM较难，因为学生不一定能理解CM=AC-AM.基于这样的现实，若用轨迹思想去思考，则问题就变得明朗起来.因为线段的长度取决于线段两个端点的位置，此题中动线段CM的两个端点“一定一动”，于是想到先作出动点M的运动轨迹，再仔细观察图中的规律，则问题的解决方案近在咫尺.

三、作全等，借“图”的形象化难为易

全等三角形是初中几何的重要内容之一，也是研究其他几何图形的基础.许多几何问题若能通过添加辅助线构造出全等三角形，以联通题设与结论，并灵活运用全等图形的相关性质，往往可以使问题化难为易，进而快速找到解决问题的方法.

例3如图4，在矩形ABCD中，AB=3,AD=4, 点E，F分别是边BC和对角线BD上的动点，且始终保持BE=DF,连接AE和AF.当线段AE+AF的值最小时，求的值.

图4

解析：如图5，以点B为顶点，BE为一条边向矩形ABCD外作∠GBE=∠ADF,并在∠GBE的一边上截取BG=AD,连接BG，则△BGE≌△DAF.所以EG=AF.从而将AE+AF转化为AE+EG.此时不难发现，当点A，E，G三点共线时，线段AE+AF的值最小（如图6）.

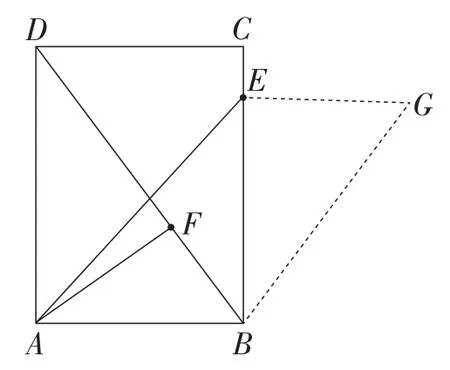
图5

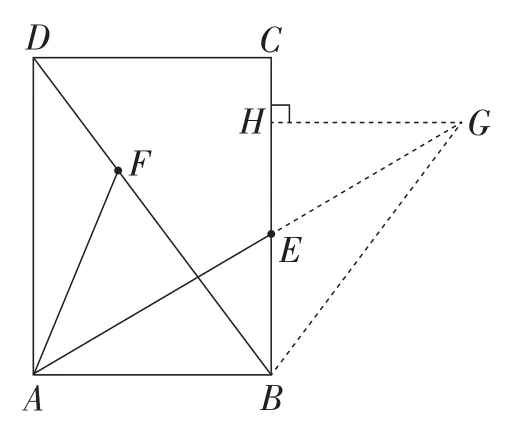
图6

此题通过作全等三角形，实现线段的转移和拼接，同时将定点A转化为定点G，巧妙地将“两动一定”转化为“两定一动”.于是利用“两点之间线段最短”的基本事实可以发现：当A，E，G三点共线时，AE+EG的值最小，即AE+AF的值最小.至此，离问题的最后解决仅一步之遥，后续只需要构造相似三角形，便能实现问题的真正解决.这种先作图后计算的思维策略相比其他思维策略要简明许多.例如，此题也可以采用先计算后作图的思维策略，但解答的过程却是一路艰辛.

设BE=DF=x,则如图7，过点F作FG⊥AD于点G，易知.进而得到.所以.

图7

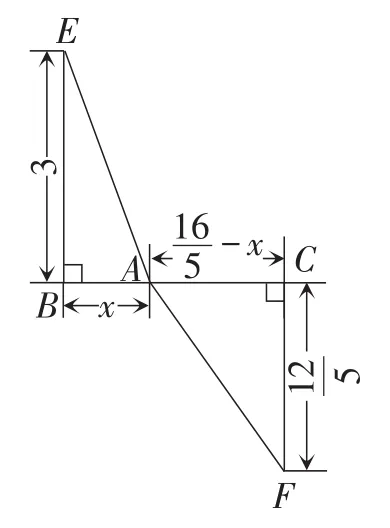
图8

至此，用代数方法解答陷入困境，后续解答需要图形来帮忙，即先将变形为再构造如图8所示的图形，方能找到正解.

四、作反例，凭“图”的真相去伪存真

我们知道，严谨的证明既可以肯定一个命题的真，也可以判定一个命题的假.只是有些时候用逻辑推理的方法去证明一个假命题，不仅耗时费力，而且也不一定能想到证法.此时，若能用作图的方式举一个巧妙的反例，就能凭“图”的真相去“伪”存“真”.正如美国数学家B.R.盖尔鲍姆所说：数学由两大类——证明和反例组成，而数学发现也是朝着两个主要目标——提出证明和构造反例进行.例如，对一个数学命题的判断，正确需要证明，谬误反例足矣.

例4判断命题“一组对角相等且一组对边也相等的四边形是平行四边形”的真假，并说明理由.

解析：假命题.理由如下.

列举反例如下：如图9，先作锐角△ABC，并在BC边上取一点D，使AD=AC,再过点C作∠1=∠2,并截取CE=AB,连接AE.在四边形ABCE中，容易发现∠B=∠E,CE=AB. 但根据“图”的直观事实，显然四边形ABCE不是平行四边形.

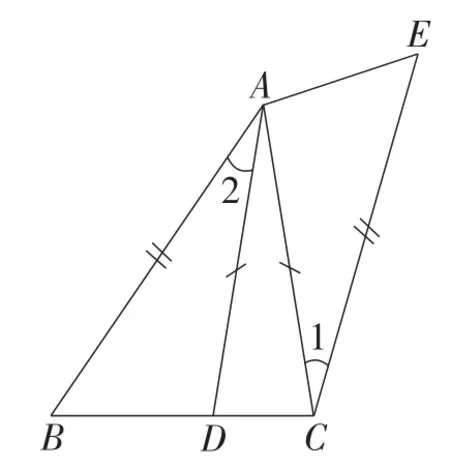
图9

此题用纯粹的逻辑推理来证明命题的真假，显然存在较大困难.因此，数学解题时要选择简明合理的方法去解决问题，就像此题的解答，用列举一个反例图的方法，凭着“图”的真相极具说服力地指出了命题的真假，也让知识在直观中去伪存真.

综上所述，准确而巧妙的作图能够帮助学生快速、准确地找到解决问题的方法.作图不仅能为解题提供直观的图形条件，还能提供形象的操作思路，是数学解题的好帮手.通过作图可以帮助学生更清楚地认清图形结构，更快捷地找到已知条件与待求结论之间的纽带，从而使复杂的问题变得简明、形象，进而发现解决问题的思路.因此，在教学中，教师应帮助学生养成几何作图的习惯，以形助数，变抽象为直观，使学生做到思之有形，真正了解图形的形成过程，发现图形中蕴含的数学方法，以及其为获取正确解题思路等方面带来的益处.