基于数学文化视角下的中考试题分析与教学建议

（安徽省舒城县阙店乡中心学校；吉林省吉林市第八中学）

通过研究2018年全国各地区150多份中考数学试卷，我们发现数学文化在试卷中主要是以以下六种方式体现的：渗透数学史；渗透中外数学名题、名图；渗透数学精神；渗透数学美；渗透数学应用；渗透数学语言.其中，把数学史作为数学文化的载体，以数学史为背景进行命题是中考试题渗透数学文化的一个非常重要的特色.下面以2018年部分中考数学试题为例进行说明.

一、中考命题中数学文化取材路径分析

1.数学史在中考试题中的渗透

在众多古代数学名著中，《九章算术》备受命题者青睐.命题者从《九章算术》中选取与当今初中数学教学内容相关的题材为背景，加上简短翻译，以选择题、填空题、解答题的形式出现在中考试卷中.下面让我们一起浏览我国古代悠久的数学发展历史，欣赏其辉煌的成就.

（1）春秋前——中国古代数学的萌芽.

例1（湖北·恩施卷）我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳记数”.如图1，一位妇女在从右到左依次排列的绳子上打结，满六进一，用来记录采集到的野果数量.由图1可知，她一共采集到的野果数量为_____.

图1

解析：由题意可知，从右到左依次排列的绳子分别代表绳结数乘以6的0次幂，6的1次幂，6的2次幂，6的3次幂，6的4次幂.她一共采集到的野果数为2×60+0×61+3×62+2×63+1×64=1 838.

【赏析】这道题目以中国古代的“结绳记数”为背景，应用学生熟悉的十进制记数法，利用类比思想，可以获得满六进一的感性认识，进而得出妇女一共采集到的野果数量.

（2）战国至两汉——中国古代数学框架体系的形成.

战国时期的百家争鸣促进了数学的发展.中国古代数学体系形成于秦汉时期，以《九章算术》为代表的数学著作的出现标志着算术已成为一个专门的学科.

例2（湖北·十堰卷）我图古代数学著作《九章算术》卷七有下列问题：“今有共买物，人出八，盈三；人出七，不足四，问人数，物价几何？”意思是：现在有几个人共同出钱去买物品，如果每人出8钱，则剩余3钱；如果每人出7钱，则差4钱，问有多少人，物品的价格是多少？设有x人，物品的价格为y元，可列方程（组）为（ ）.

解析：设有x人，物品的价格为y元，根据每人出8钱，剩余3钱，则物品的价格为y=8x-3;如果每人出7钱，差4钱，则物品的价格为y=7x+4,可列方程组

【赏析】此题的背景源于《九章算术》中的第七章“盈不足”问题，考查学生利用方程（组）解决实际应用中的盈亏问题的能力，注重渗透应用数学的意识，培养学生的数学建模素养.

例3（湖北·荆州卷）《九章算术》是中国传统数学名著，其中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两.问牛、羊各直金几何？”译文：“假设有5头牛，2只羊，值金10两；2头牛，5只羊，值金8两.问每头牛、每只羊各值金多少两？”若设每头牛、每只羊分别值金x两、y两，则可列方程组为（ ）.

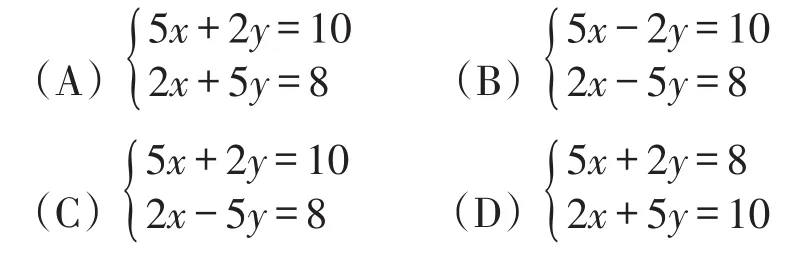
解析：由牛5头，羊2只，共值金10两，得5x+2y=10；由牛2头，羊5只，共值金8两，得2x+5y=8.故可列方程组为

【赏析】此题的背景源于《九章算术》中的第八章“方程”问题，考查学生利用方程组解决实际问题的能力，注重渗透应用数学的意识，培养学生的数学建模素养.应用同样的背景，2018年江西省中考数学试卷第9题以填空题的形式考查了列方程组的问题.《九章算术》方程章中的“方程”是专指多元一次方程组而言，与现在教材中方程的含义并不相同.《九章算术》中多元一次方程组的解法，是将它们的系数和常数项用算筹摆成“方阵”（所以称之为“方程”）.

（3）魏晋至唐初——中国古代数学理论体系的建立与发展.

魏晋时期，中国古代数学在理论上有了较大的发展.赵爽撰写的《周髀算经注》，其中用600余字概括了两汉以来勾股算术的成果.刘徽注释《九章算术》，撰写《海岛算经》，创造割圆术，利用极限思想证明圆的面积公式，并首次用理论的方法算得圆周率.

例4（安徽卷）《孙子算经》中有这样一道题，原文如下：“今有百鹿入城，家取一鹿，不尽，又三家共一鹿，适尽.问：城中家几何？”大意为：今有100头鹿进城，每家取一头鹿，没有取完，剩下的鹿每3家共取一头，恰好取完.问：城中有多少户人家？请解答上述问题.

解析：设城中有x户人家，根据题意列出方程x+.解得x=75.

【赏析】《孙子算经》是中考命题者喜爱的另一本数学典籍，给出了筹算记数制度及乘除法则等预备知识，其中的“河上荡杯”“鸡兔同笼”等问题后来在民间广泛流传.《张丘建算经》中的“百鸡问题”引出了不定方程组问题.

（4）唐中叶至宋元——中国古代数学空前繁荣.

唐中叶至宋元时期是中国古代数学空前繁荣、硕果累累的全盛时期.宋元时期的数学在很多领域都达到了中国古代数学（甚至是当时世界数学）的巅峰.这一时期出现了一批著名的数学家和数学著作.例如，贾宪撰写的《黄帝九章算法细草》，秦九韶撰写的《数书九章》，书中共列算题81问，分为9类.《数书九章》是对《九章算术》的继承和发展.

例5（山东·德州卷）我国南宋数学家杨辉所著的《详解九章算术》一书中，用如图2所示的三角形解释二项式(a+b)的n展开式的各项系数，此三角形称为“杨辉三角”.

图2

根据“杨辉三角”，试计算(a+b)的8展开式中从左起第四项的系数为（ ）.

（A）84 （B）56 （C）35 （D）28

解析：通过找规律，发现(a+b)的4第四项系数为4，4=3+1;(a+b)的5第四项系数为10，10=6+4;(a+b)6的第四项系数为20，20=10+10;(a+b)7的第四项系数为35，35=15+20.所以(a+b)的8第四项系数为21+35=56.

【赏析】“杨辉三角”又称贾宪三角形，帕斯卡三角形，是二项式系数在三角形中的一种几何排列.此题考查了数字变化规律，考查学生通过观察、发现、分析、归纳其中的规律，并应用发现的规律解决问题的能力.

（5）明清数学——从衰落到艰难的复兴中与西方数学融合.

明代最大的成就是珠算的普及，出现了许多珠算读本.程大位的《直指算法统宗》问世，珠算理论已成系统，标志着从筹算到珠算转变的完成.但由于珠算流行，筹算几乎绝迹，建立在筹算基础上的古代数学也逐渐失传.在西方传入的数学中，影响最大的是中国第一部数学翻译著作欧几里得的《几何原本》，其中大部分数学名词都是首创，许多至今仍在沿用，其次应用最广的是三角学.

例6（湖南·邵阳卷）程大位是我国明朝商人，珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著，详述了传统的珠算规则，确立了算盘用法.书中有如下问题：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁.”意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，大、小和尚各有多少人？下列求解结果正确的是（ ）.

（A）大和尚25人，小和尚75人

（B）大和尚75人，小和尚25人

（C）大和尚50人，小和尚50人

（D）大、小和尚各100人

解析：根据题意可以列出方程,解得x=25.则100-x=100-25=75（人），所以大和尚25人，小和尚75人.

2.数学美在中考试题中的渗透

美学的四大构件分别是史诗、音乐、造型（绘画、建筑等）和数学.因而数学教育是审美素质教育的一部分.中国古代著名哲学家庄子说：判天地之美，析万物之理.在中考试题中有很多数学美在等待着我们发现.

（1）对称美.

例如，山东济南卷第4题的中国古建筑装饰檐头的附件“瓦当”，内蒙古通辽卷第2题的剪纸艺术，湖南永州卷第2题以全国第三大露天碑林的“浯溪碑林”中的汉字为例识别轴对称图形，这些文化背景给人以美的享受，陶冶审美意识，弘扬着中国悠久的文化艺术，散发着浓郁的数学美的气息，也激发着我们的爱国之情.

（2）和谐美.

几何中，我们学过“黄金分割”，即把线段l分成x和l-x两段，使其比满足x∶l=(l-x) ∶x,解得x≈0.618l,这种分割称为“黄金分割”.0.618…是被中世纪学者、艺术家达·芬奇誉为“黄金数”的重要数值，它也曾被德国数学家开普勒赞为几何学中两大“瑰宝”之一.（另一件为“勾股定理”.）

17世纪的英国美学家夏里兹曾说：“凡是美的都是合谐的和比例合度的；凡是和谐的和比例合度的就是真的，凡是既美而又真的也就是在结果上愉快和完善的”.例如，云南昆明卷第9题以黄金分割数为背景，山东德州卷第24题以黄金矩形为背景，山西卷第12题以窗格上的冰裂纹图案为背景，这些试题都在展示着数学的和谐美.

3.数学应用意识在中考试题中的渗透

以数学故事、数学游戏为背景设计的中考试题举例如下：湖北黄石卷第16题以“石头、剪子、布”游戏为背景，设计利用一元一次方程求得分的问题，福建B卷第8题“绳索量竿”问题，浙江金华卷第16题以弓箭为背景考查垂径定理和圆的有关计算，四川绵阳卷第14题以中国象棋为背景考查点的坐标，湖北随州卷第7题以“龟兔赛跑”为背景考查函数图象的问题.

以社会生活、社会热点为背景设计的中考试题举例如下：河南卷第20题以“高低杠”为背景考查解直角三角形，四川绵阳卷第9题求蒙古包面积，江西卷第19题以折叠门为背景考查轨迹、等边三角形、弧长公式，浙江绍兴卷第8题以二维码身份识别为背景考查记数问题，湖北荆门卷第20题以央视推出的《中国诗词大会》《中国成语大会》《朗读者》《经典咏流传》等一系列文化栏目为背景，考查统计图表和概率，内蒙古呼和浩特卷第2题以二十四节气为背景考查函数图象.

二、关于数学文化教学的几点建议

通过仔细研究2018年全国各地区中考数学试卷，对今后的教学和中考复习提出以下建议.

1.善于挖掘教材中的数学文化

作为数学教师，要熟读《义务教育数学课程标准（2011年版）》，它是指导教学的理论基础与教学指南；要重视教材中的“引言”“阅读与思考”部分，这部分内容富含数学文化，要善于挖掘并充分利用这部分内容，开展数学文化在课堂教学中的渗透.同时，还要阅读数学史来了解中国的数学历史文化，并且有针对性地运用到课堂教学中，积极营造浓厚的数学文化氛围，引导学生重视数学文化，从而提高学生学习数学的兴趣，弘扬我国优秀的传统文化，不断提升自身的数学文化素养.

2.重视对数学文化类试题的研究

数学文化可以体现在各个方面，数学命题仅仅是它的一个方面.将数学文化和命题有机结合，注意引导学生在运用数学知识解决问题的同时，深挖试题中蕴含的数学文化，通过解决问题来传播数学文化.这样不仅能消除学生对该类试题的陌生感，而且还可以帮助学生更好地了解数学文化，领悟数学思想方法和魅力，有效落实“立德树人”的根本任务.

对于经典名题、名图类的试题，可以在解题中体会其中隐含的数学知识，挖掘出题目中的已知条件，明确考查的知识点，探索解题思路，从而有效地解决问题.

总之，教师要深入研究历年中考试题，挖掘试题中所蕴含的相关数学文化和数学精神，并在课堂教学中灵活渗透.这样，不仅能激发学生学习数学的兴趣，也能使数学不再枯燥乏味.当数学文化的魅力真正渗入命题、到达课堂、融入教学时，数学就会更加平易近人，数学教学就会借助数学文化让学生进一步理解数学、热爱数学.