试题是例题的“化身”
——从一道中考模拟题的命制谈起
(浙江省杭州市春蕾中学)
笔者曾有幸参与浙江省杭州市(区)九年级中考模拟试卷的命制工作,颇有感触.现以其中的一道试题为例,谈谈如何将教材例题改编成试题.
一、背景分析
1.根据考点寻找例题
根据试卷双向细目表安排,试卷第10题为选择题,涉及的知识点是平行线、角平分线、平移等,考查学生对平行线和角平分线等知识的综合运用能力.根据试题立意,命题组选择浙教版《义务教育教科书·数学》(以下统称“教材”)七年级下册“1.3平行线的判定”(第2课时)中的例4作为题源开展研究.例4内容如下.
题源如图1,AP平分∠BAC,CP平分∠ACD,∠1+∠2=90°.判断AB,CD是否平行,并说明理由.
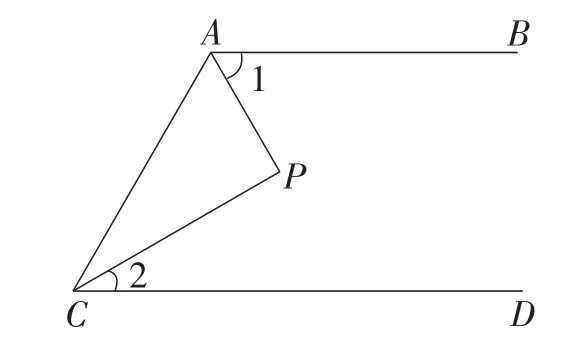
图1
该题涉及的数量关系和位置关系有∠1+∠2=90°,∠BAC+∠ACD=180°,∠1+∠2=∠P,AP平分∠BAC,CP平分∠ACD,AB∥CD等.
该中考模拟卷第10题要考查学生对数学本质的理解和学以致用的能力,显然在考查知识点的深度和广度上还需要进一步探索.经过分析,命题组决定借助图形中多样的角度关系,在角度、角度的比值之间进行深入研究,期待找到命题的生长点.
2.根据学情助力思维
在第三学段中,从七年级下册开始,教材中频繁出现类似于题源的题目,这些题目有三个共同点:平行线,一对同旁内角的平分线,90°角.教材八年级上册“1.3证明”(第1课时)的例2是题源的逆命题;八年级上册“2.6直角三角形”(第2课时)作业题A组第3题是在题源的基础上,通过延长AP,CP得到三个直角三角形;八年级下册“4.2平行四边形及其性质”(第2课时)作业题B组第5题是将三个共同点放置于平行四边形背景中.从七年级下册开始出现,到八年级上册,再到八年级下册,从平行线到三角形再到四边形,题源为学生积累了丰富的知识基础和思维活动经验.
无论是背景的置换,还是新元素的加入,在不断变化和发展中的题源,渐渐从特例演变成模型,其数学本质愈发凸显.命题者若能深入剖析题源,进而得到一般性的规律,再从规律中引出更多的特例,这样的命题是将例题一般化和特殊化相结合,在帮助学生继续深化基础知识的同时,连接了特殊化和一般化的关系,培养了学生的思维品质,发展了思维能力.
二、命题过程
1.题源一般化
如图2,AB∥CD,点P在AB,CD之间,连接AP,PC,AC,点P在AC右侧.假设∠BAP=x°,∠CAP=mx°,∠DCP=y°,∠ACP=ny°,∠P=z°,0°<x,y,z<180°,m,n>0.试探究m,n,z之间的数量关系.
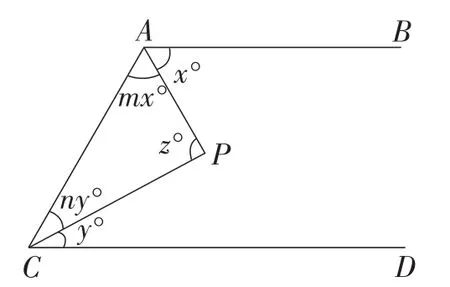
图2
解:由题意,得
消去x,得(n-m)y=180-(m+1)z.
在0°<y,z<180°,且m,n>0 的范围内讨论,可得:
当m=n>0时,;
当m>n>0时,;
当0<m<n时,.
消去y,得(m-n)x=180-(n+1)z.
在0<x,z<180, 且m,n>0 的范围内讨论,可得:
当m=n>0时,;
当m>n>0时,;
当0<m<n时,.
综上所述,可得如下结论:
(1)当m=n>0时,;
(2)当m>n>0时,;
(3)当0<m<n时,.
进一步变形,可得如下结论:
(4)当m=n>0时,;
(5)当m>n>0时,;
(6)当0<m<n时,.
2.命题生长源
结论(1)(2)(3)是命制此道模拟试题的生长源.z的取值范围由决定,进一步是由m和n决定.当且仅当m=n>0时,z的值是唯一确定的.例如,当m=n=1时,z=90,此时∠P是直角.当m≠n时,z的取值范围介于之间;当|m-n|越小时,z的取值范围越小;当|m-n|越大时,z的取值范围越大.例如,当n=1,m=2时,60<z<90,∠P是锐角;当n=5,m=0.8 时,30<z<100,∠P可以是锐角、直角或钝角.通过调节m,n的大小,就可以影响∠P的大小,命题者可以“调数控形”了.
结论(4)(5)(6)也是命制此道模拟试题的生长源.当n和z的值确定了,n和的大小也随之确定,那么m的取值范围是中的一种.当且仅当时,m的值是唯一确定的(例如,当n=3,z=45时,m=3).当时,,m的值是不唯一的(例如,当n=1,z=60 时,m>2).当时,,m的值是不唯一的(例如,当n=1,z=100时,0<m<0.8).通过调节m,n中的一个比值和∠P的大小,就可以影响另一个比值的大小,命题者可以“调形控数”了.
从教材例题出发,针对例题进行一般化探究后,得到了六个关于m,n和z的相等或不等关系,这六个不同的数量关系还可以特殊化,这些都为命题者提供了可以挑选的不竭资源.
3.命题策略
步骤1:保留一般化.
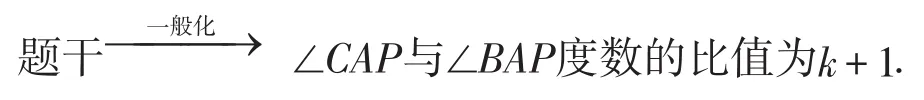
保留一个角度比值的一般化是期望在题源的基础上,引导学生往一般规律进行探索的重要手段.其中一个角度的比值设为k+1而不是k,是因为在计算过程中k+1能够巧妙地减少计算量.这样的命题既增加了思维量,又控制了计算量.
步骤2:赋值特殊化.
该模拟试题中有四个命题需要判断是否正确,四个命题分别由一般化结论赋值特殊化而来.
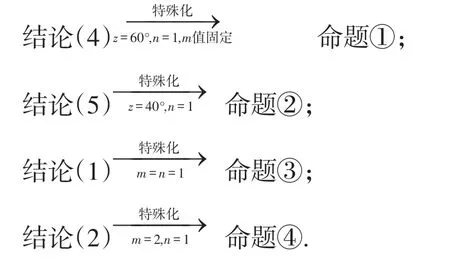
以一般化结论为蓝本,取四个特例,使该模拟试题变得多滋多味.命题①是从特殊角度推算特殊比值,入口较宽,有利于学生对于基本解法的探索;命题②构造了一个正确的特例,以便让师生能揭开此题最大悬念,激发学生探究两个角度的比值和∠P之间规律的兴趣;命题③是从特殊比值向特殊角度逆推;命题④设置需要分类讨论的等腰三角形作为结论,这与∠P本身是可变的具有匹配的可能性.命题②较命题①,命题④较命题③呈现递进式问题设置,命题①②较命题③④呈现顺逆式问题设置.
步骤3:化身成题.
模拟试题如图3,AB∥CD,点P在AB,CD之间,CP平分∠ACD,连接AP,∠CAP与∠BAP的度数的比值为k+1.下列结论:①当∠P=60°时,k=2;②当∠P=40°时,;③当k=0时,△ACP一定是直角三角形;④当k=1时,△ACP一定是等腰三角形.其中正确的结论是( ).
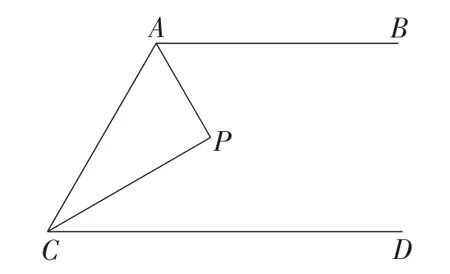
图3
(A)①② (B)②③
(C)②③④ (D)③④
参考答案:B.
该题的题干是在题源的基础上对于一对角度的比值进行了一般化,四个命题是在一般化结论中对∠P、角度的比值、△ACP进行了特殊化.经历定量计算和定性分析,一般化和特殊化相互作用,双向理清角度之间的关系,显露数学问题的本质.通过问题驱动,层层递进,加深学生对于数学知识本质的理解,正确处理一般化和特殊化的关系,提高灵活迁移的效率.
三、命题反思
命题者从教材出发,根据考点,寻找匹配程度较高的例题作为题源,再针对题源进行一般化研究,寻求蕴含的数、形规律,最后从研究成果中选取一部分精华编制成模拟试题,如此这般,一道中考模拟题就新鲜出炉了.此类试题的命题策略一般包含以下三个方面.
1.以本寻根,题海弃之
从教材出发,根据要考查的知识点,寻找匹配程度较高的例题,筛选出的例题应包含基本图形、基本模型或基本思想方法,具有典型性,可以是一个,也可以是多个,以便为下一步探究使用.众所周知,在中考复习阶段,回归教材才能有效减轻学生的负担,追根溯源,夯实基础,才能展开灵活的综合运用.该模拟试题中熟悉的几何直观,融合了理性的思考,周密的计算,将初中阶段多个核心知识点融合在一起,此试题是对教材例题的继承和发展.
2.例题为干,一般化之
教材中的例题(题源)涉及多个角,多种数量关系和位置关系,彼此之间相互关联,相互制约,通过抽丝剥茧,确定将两个角度的比值和∠P作为研究对象,将三者和谐统一在一个及其常见的图形当中,其中必隐含数、形规律.命题者充分挖掘典型教材例题的潜能,洞悉图形的自然规律,从特殊到一般不断探索,得出的六个结论让人不禁赞叹.将教材例题一般化研究后,可以变化出一类题目,无论是特殊的,还是一般的,都包含有教材例题的通性、通法,这类题目将成为下一步命制试题的源泉.
3.开花结果,优而取之
按照《义务教育数学课程标准(2011年版)》和考试大纲对相关知识点的要求,在六个结论中择优录用,汇制成题,方法兼顾一般和特殊.该模拟试题中,将题干中两对角度的比值一般化,四个命题涉及角度特殊化、比值特殊化、图形特殊化,如此优化设置后就得到了四个或真或假的命题.试题行文简洁,背景熟悉,角度新颖,层次分明,综合性强,包含数学核心知识,渗透了多种数学思想方法,考查了学生的多项能力.至此,一道经典的教材例题华丽转身成为一道中考模拟试题.这样的试题往往是源于教材,又高于教材的.
总之,此类试题可谓是教材例题一般化和特殊化的“化身”.深入研究例题后,带给命题者以灵感,从一开始的一般化到之后的特殊化,成为命制试题的宝藏.同时,饱含一般化和特殊化元素的试题为学生提供了从特殊到一般,从一般到特殊的双向训练,助力学生思维水平和数学推理思想的提升.这种命制试题的经历给命题者提供了一种有效的命题策略.

