深剖已知条件 寻求思维起点——以一道几何竞赛题的多解思路分析为例

（浙江省湖州市南浔区教育教学研究和培训中心）

罗增儒教授曾在《中学数学解题的理论与实践》一书中提到：掌握数学的一个重要标志就是善于解题，会解题的不知道怎么就会了，不会解题的更不知道怎么就老学不会.可谓是一语惊醒广大数学教育工作者，特别是后半句——“不会解题的更不知道怎么就老学不会”.相信这也是数学教师在解题教学时的心声.那么，如何才能有效解决这一普遍现象呢？笔者认为，当学生遇到问题时，如何快速浮现数学表象，以及顿时产生数学直感非常重要，即如何深入剖析问题的已知条件，从而直观想象，并通过解题经验寻求思维起点，进而解决问题.本文从一道几何竞赛题的多解思路分析来谈一谈笔者对解题教学的一些粗浅的认识，权当抛砖引玉.

一、题目呈现

题目（2016年浙江省湖州市九年级数学竞赛题）如图1，已知AD为△ABC的角平分线，AB＜AC，在AC上截取CE=AB，M，N分别为BC，AE的中点.求证：MN∥AD.

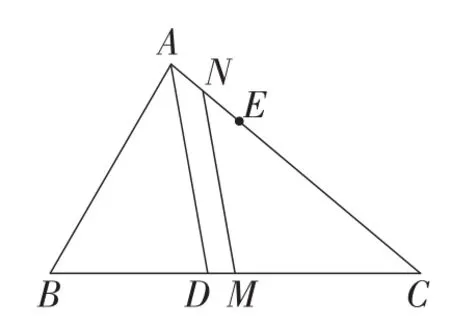
图1

二、试题评析

该题是一道对学生的逻辑推理能力要求较高的几何证明题，图形和已知条件看似简单，但剖析已知条件发现线段之间的关系错综复杂，因此，学生解决起来有一定的困难.该题综合性较强，涉及的主要知识点可能有全等三角形、相似三角形的性质与判定，角平分线的性质与意义，三角形中位线判定与性质，梯形中位线判定与性质，平行线的判定与性质，平行线分线段成比例，平行四边形的判定与性质，等腰三角形“三线合一”，等等.需要用到的数学思想可能有转化思想、方程思想、数形结合思想等.

三、多解思路分析

即便是具备较高思维层次的学生遇到该题，都会感觉不知所措，从何想起？换言之，该题的思维起点到底在哪里？不妨深入剖析一下该题的每一个已知条件，这些已知条件均有可能成为重要的思维起点，有了思维起点，就能逐步打通整个解题思路.接下来，笔者就从不同的已知条件出发进行深入剖析，从而正确地寻求该题的思维起点，进而解决问题.

1.深剖中点条件，寻求中位线思维起点

（1）构造三角形的中位线.

解法1：取AB中点F，连接MF，交AD于点G，如图2所示.

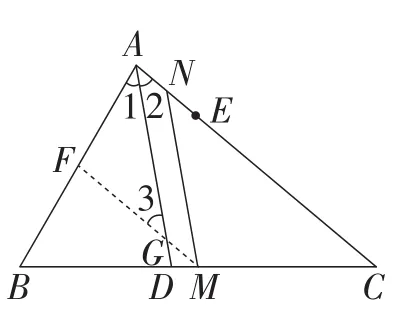
图2

所以∠1=∠2=∠3.

所以GM=AN.

所以四边形AGMN为平行四边形.

所以MN∥AD.

解法2：取AC中点F，连接MF，如图3所示.

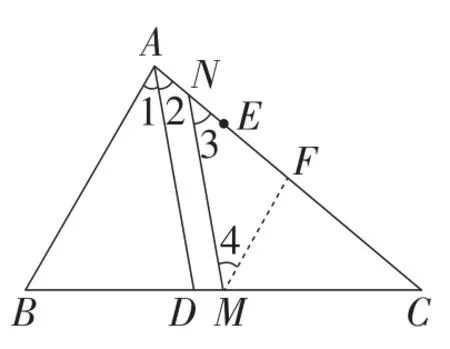
图3

同解法1，得FM∥AB，

所以FM=FN.

所以∠3=∠4.

由∠MFC=∠BAC，得∠1+∠2=∠3+∠4.

又因为∠1=∠2，

所以∠1=∠2=∠3=∠4.

所以MN∥AD.

解法3：连接BE，取BE中点为点F，连接FN，FM，如图4所示.

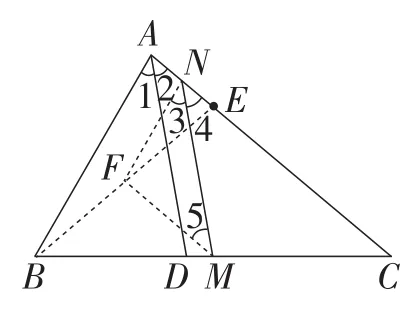
图4

因为FN为△EAB的中位线，

因为CE=AB，

所以FN=FM.

所以∠3=∠5=∠4.

因为∠1=∠2，∠1+∠2=∠3+∠4，

所以∠2=∠4.

所以MN∥AD.

【评析】解法1和解法2这两种思路的本质相通，均是由已知条件中的“M为BC的中点”所联想到；解法3是由已知条件中的“CE=AB，M，N分别为BC，AE的中点”所联想到，形成了正确的思维起点，即由三角形某边的中点，联想到了构造三角形中位线.解法1通过三角形中位线，以及已知的线段相等关系证得平行四边形，利用平行四边形的性质证得结论.解法2通过三角形中位线及已知的线段关系，利用数量关系的转化证得同位角相等，从而结论成立.解法3利用两条三角形中位线的构造巧妙的将条件“CE=AB”转化为“FM=FN”，从而利用角关系之间的转化，进而利用平行线的判定方法解决.这三种解法均是通过深入剖析已知条件“CE=AB，M，N分别为BC，AE的中点”和所证结论“MN∥AD”之间的关联，找准了“作三角形中位线”来作为此题的逻辑思维起点，为解决问题迈出了坚实的一步.

（2）构造梯形的中位线.

解法4：在BC上取一点F，使得MF=MD，如图5所示.

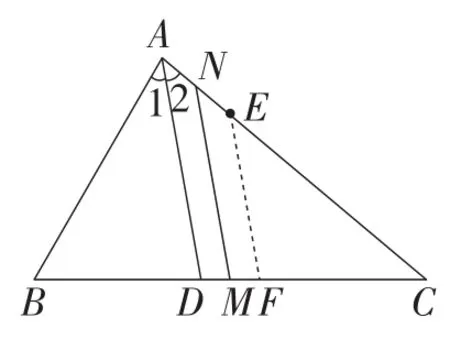
图5

则由M为BC的中点，可得CF=BD.

由∠1=∠2，可得

可证得EF∥AD.

因此，四边形ADFE是梯形.

故MN是该梯形的中位线.

所以MN∥AD.

解法5：过点E作EF∥AD，交BC于点F，在AD上取点G，使得AG=EF，连接BG，如图6所示.

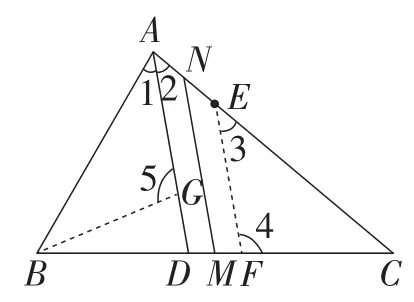
图6

易证△ABG≌△ECF.

所以BG=CF，∠5=∠4.

所以∠BGD=∠BDG.

所以BD=BG=CF.

由M为BC的中点，可得

MD=MF.

故MN是梯形ADFE的中位线.

所以MN∥AD.

解法6：过点E作EF∥AD，交BC于点F，过点B作BG∥AC，交AD的延长线于点G，如图7所示.

易得∠1=∠2=∠3=∠G.

所以AB=BG=EC.

又因为∠GBD=∠C，

所以△BDG≌△CFE.

所以BD=CF.

下同解法4，略.

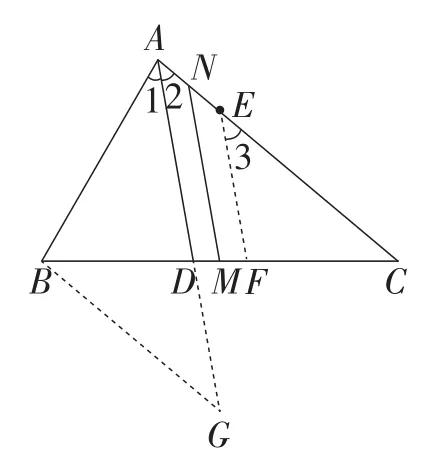
图7

【评析】解法4通过角平分线定理证得平行，从而满足了梯形中位线的条件.解法5和解法6思路相通，解法5是从内部构造全等三角形，而解法6是从外部去构造全等三角形，这两种解法都是通过构造全等三角形来得出相等的线段，从而满足梯形中位线特征.解法4主要通过剖析已知条件“M，N分别为BC，AE的中点”和所证结论“MN∥AD”的直接关联，联想到“构造梯形中位线”的思维起点.解法5和解法6则是深入挖掘已知条件中的“M，N分别为BC，AE的中点”和“CE=AB”的内在联系，从而确定了“构造梯形中位线并证全等三角形”的逻辑思维起点.

2.深剖中点条件，寻求全等三角形思维起点

解法7：延长NM至点F，使得MN=MF，连接BF，延长AD交BF于点G，如图8所示.

图8

易得△BMF≌△CMN.

所以BF=CN，且BF∥AC.

所以∠1=∠2=∠3.

所以BG=AB=EC.

所以BF-BG=CN-EC，

即GF=NE.

所以GF=AN.

所以四边形AGFN是平行四边形.

所以MN∥AD.

【评析】解法7是由已知条件中的“M为BC的中点”所形成的思维起点，当然还需要学生具备这样的解题经验——“遇中点，可倍长”，即看到中点，可将经过中点的线段延长一倍，根据“边角边”的判定方法构造出一对全等三角形，利用全等三角形的性质解决问题.可见，线段中点作为已知条件时，有时亦可寻求全等三角形作为思维起点.

3.深剖角平分线条件，寻求等腰三角形思维起点

（1）利用“三线合一”构造等腰三角形.

解法8：过点B作BF⊥AD于点F，并延长BF，交AC于点G，连接MF，如图9所示.

由∠1=∠2，BF⊥AD，可得△ABG是等腰三角形.

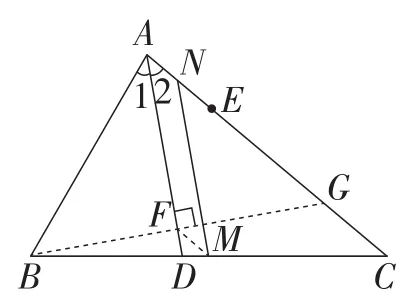
图9

所以AB=AG，BF=GF.

所以MF是△BCG的中位线.

所以MF∥AC，且

又因为CE=AB=AG，

所以CE-EG=AG-EG，

即CG=AE.

所以FM=AN.

所以四边形AFMN是平行四边形.

所以MN∥AD.

【评析】解法8的思维起点是通过分析已知条件中的“AD为△ABC的角平分线”联想到：遇到角平分线时可作垂直构造高线，从而利用等腰三角形“三线合一”定理的逆定理即能得出两个重要的结论，即构造一个等腰三角形和一条底边上的中线，进而利用三角形中位线的判定与性质，以及平行四边形的判定与性质证得结论成立.因此，只要让学生具备“遇角平分线，可作垂直构造等腰”的解题经验，相信该题的解题思路必将一路畅通.

（2）利用“双平等腰问题”构造等腰三角形.

解法9：过点B作BF∥AD，交CA的延长线于点F，如图10所示.

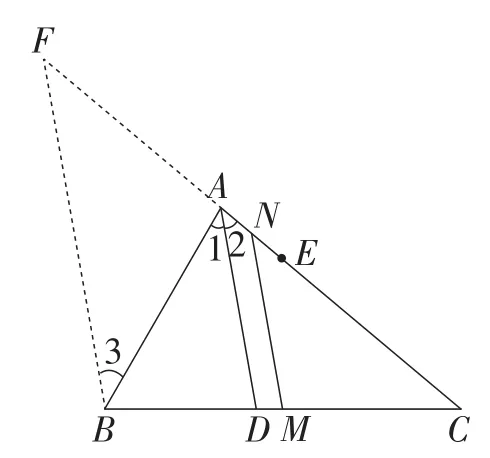
图10

因为BF∥AD，

所以∠1=∠3，∠2=∠F.

又因为∠1=∠2，

所以∠F=∠3.

所以AB=AF.

所以EC=AF.

因为AN=NE，

所以FN=CN.

所以MN是△BCF的中位线.

所以MN∥BF.

所以MN∥AD.

【评析】解法9的思维起点同样源于已知条件中的“AD为△ABC的角平分线”，遇到角平分线时也可联想到“双平等腰三角形”问题，即“角平分线+平行→等腰三角形”，简称为“双平等腰问题”.该思路通过巧妙地构造出等腰三角形ABF，从而得出MN是△BCF的中位线，最后利用平行线的传递性证得结论成立.可见，由条件中的角平分线联想到的“双平等腰三角形”模型可以让该题的解决更轻松简洁.其实，解法1、解法5、解法6也都渗透着“双平等腰问题”的运用.可见，学生如对于“双平等腰问题”理解透彻的话，能够寻求到可以解决该题的多种思维起点.

4.深剖角平分线条件，寻求比例线段思维起点

解法10：设AB=CE=a，AN=NE=b，如图11所示.

图11

由AD为△ABC的角平分线，可得

【评析】解法10是以上解法中唯一不需要添辅助线的解法，其思维起源于已知条件中的“AD为△ABC的角平分线”.根据三角形角平分线定理可以得到比例线段，再根据条件中的线段相等及线段中点等重要信息设出辅助元，进而利用比例线段证得结论成立.该思路虽然无需添加任何辅助线，但是对于比例线段的处理要求较高，因此也是不易想到的一种解题思路，但如能从角平分线这一条件进行突破，也还是能想到该思路的.

四、两点思考

1.注重渗透解题经验，丰富学生的思维储备

《义务教育数学课程标准（2011年版）》特别强调：数学活动经验的积累是提高学生数学素养的重要标志，帮助学生积累数学活动经验是数学教学的重要目标，是学生不断经历、体验各种数学活动过程的结果.这里的“解题经验”包括解题思想方法、解题基本模型、解题通法或技巧等规律方面的思维能力.如上述提到的“遇中点，想中位线”“遇中点，构全等”“遇角平分线，构等腰”等.另外还有没提到的，但是大家在平时的教学中也时常会渗透的.例如，“遇垂直，想勾股”“遇切点，连圆心”“遇90°圆周角，找直径”等.同时，一些常见的几何基本问题也属于解题经验范畴，如“双平等腰问题”“将军饮马问题”“三垂直问题”“半角问题”“共顶点旋转问题”等.我们如能在平时的教学中多渗透这样的“解题经验”，就能丰富学生的思维储备，为思维起点的顿悟铺好扎实的基石.

2.深入剖析已知条件，快速找准思维起点

分析问题，寻求思路的方法一般有三种：由因导果，执果索因，因果夹击.本文重点探索“由因导果”的思维寻求方式，即从已知条件出发，一步一步推得结论成立.上述案例中介绍的十种不同的解题思维均是从某个特定的已知条件出发，找准了思维起点后最终顺利解决问题的.可见，该思维方式需要学生有一定的深入剖析已知条件的能力，以求浮现出更多的数学表象.当学生拥有足够的“解题经验”作为思维储备时，数学表象就会转化为一个有序的深化过程，进而顿悟出数学直感，即找准了某条正确思路的思维起点.数学直感的得出是解题的重大进展，它能为图形各部分数学关系的沟通起到桥梁作用，为后续的展开数学想象和给出逻辑证明铺平了思维的道路.