发挥数学之美的教育价值

汪梅

[摘  要] 追求美是人类的本能之一，美的存在能激发人们强大的内生动力，数学是一门充满着智慧和美的学科，发掘数学的美能激发学生极大的探索欲望，然而传统的教学模式中，教师和学生在重压之下都疲惫紧张，失去了感受美的精力. 文章中笔者就将谈一谈自己对数学之美教育作用的理解，并结合自身教学实践经验和各位读者分享在课堂中渗透数学之美的方法.

[关键词] 数学之美;数学课堂教学;合分比定理

爱美之心人皆有之，人们在生活中不断追求着美好的事物，美令人向往，令人产生强大的动力，然而人们在生活中提到的美——山水风光的自然美、华章巧奏的韵律美或五彩缤纷的视觉美，仿佛都与数学无关，数学在很多人眼中是抽象的、枯燥的，甚至是冰冷的，数学真的不美吗？当然不是，数学很美，作为自然科学的皇后，数学的美甚至可以说是絕伦的. 著名哲学家罗素也曾感叹道，数学不只是一门揭示真理的学科，如果人们能正确看待它，将会发现蕴藏其中的至高的美.

那么，数学本是一门美的学科，为什么学生感受不到它的精彩呢？笔者认为这和传统教育模式的特点密切相关. 在传统的教学模式下，教师和学生都被应试的指挥棒压得喘不过气来，教师为了提高学生的熟悉度，往往将课堂安排得满满当当，课堂节奏也因此过于紧凑，学生为了得到更高的分数，大量地做习题，题海式地学习，这样的模式给学生带来了极大的身心压力，再加上数学本身就具有较高的抽象性，学生在学习数学时很难体会到乐趣，久而久之，便会丧失对数学学习的兴趣，最直观的影响就是学习的积极性下降，学生变得被动和僵硬，体会不到数学之乐，更遑论数学之美了. 学生眼中的数学变成了负担，本该五彩缤纷的数学世界变成了枯燥的数字与符号累加.

法国数学家彭加勒曾经说过这么一句话，“科学家之所以能如此热忱地探索自然，并不是因为这样的探索能带来实用性的利益，而是因为在探索的过程中科学家们能够获得至高的快乐，而自然界中存在的美正是这份快乐的来源;如果自然没有这样诱人的美，那么它就不值得被探索了，生命的存在也没有了价值”. 这句话虽然有些极端，但却鲜明地表达了他的想法，让我们感受到了美对于人的巨大引导和激发作用. 追求美是人的本能，知道美的存在能让人产生强大的内生动力，探索美的过程能给人带来精神的满足和乐趣. 另一位数学家阿达马也说过，“我们的下意识会对自然现象或者数字关系进行大量的排列组合，这些组合中的大多数并不具有价值，也不具有美感，我们永远也不会注意到他们，存在于我们潜意识当中的几何直觉会将我们的注意力引导到少数和谐的组合上”. 这句话中的几何直觉可以理解为一种数学思维，阿达马指出了数学思维不仅是逻辑思维，而是一种逻辑与直觉的混合思维，两者相辅相成，共同促进了人们的思考. 笔者认为这两句话对我们开展数学教学也有重要的指导作用，教师应意识到数学之美对学生的启发引导作用，让学生在学习数学的过程中锻炼自己的直觉与逻辑思维，教师应改变教学策略，将数学课堂建设成美的高地，做学生探索学习的导游. 下面，笔者想结合自身的教学实践经验，和各位读者分享自己在课堂中渗透数学之美的方法.

[?]巧选例题，让学生直观地感受到数学之美

例题学习是学生数学学习的重要方式之一，通过解决例题，学生可以将零散的知识点有机地结合起来，教师可以结合具体的教学内容，精心选取兼具典型性又藏有惊喜的例题让学生练习，让学生能够在巩固知识的同时体会到数学之美[1].

数学的美形式多样，数字的排列可以成为一首诗，图案的组合可以绘出一幅画，缜密的逻辑、有规律的函数等都可以成为数学的美学元素，教师要具有慧眼和匠心，将这些美学元素挖掘出来，并将其有机地融入教学过程.

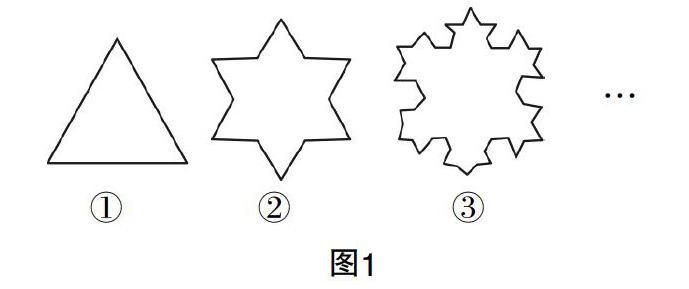
比如，教师在讲授数列的通项公式时，可以用雪花曲线的边数问题（如图1）作为例题. 雪花曲线是德国数学家科赫提出的，以一个等边三角形开始，接着在其三条边的中间位置以其边长的三分之一为边作等边三角形，以此类推. 学生在以此探索等差数列通项公式的过程中也会为图形的精美所吸引，原本枯燥抽象的数学公式仿佛也因此变得生动精彩了起来.

旅游胜地之所以吸引人，就在于世人知道它有着独特的美，教师精心选取例题，让学生在学习时感受到数学之美，能够极大地提高学生学习的积极性，学生就会像是游客一样，对数学世界产生向往之情.

[?]巧设情境，引人入胜

数学本身具有极高的美学价值，但没有好的铺垫，学生也不能完全体会到它的魅力，再拿旅游景区作比喻，旅游局为景区造势，再加以建设和改进，才能更加充分地发掘景区的美，教师在展开课堂时也要熟悉学生的心理，巧用线索，设置情境，吸引学生一步一步深入，方能使其更充分地理解到数学之美[2].

举例说明，指数函数是数学中常用的函数，其增长趋势受底数的影响很大，当底数大于1时，就算只大一点，在幂的累计下最终的结果也会非常可观，为了引出这一性质，教师可以在正式介绍指数函数之前提出这么一个问题作为情境：假设现有一张足够大的硬纸板，其厚度为2 cm，如果我们把它对折100次，其高度将会有多少？学生在经过计算之后会感叹，原本这么不起眼的两厘米在经过了一百次的折叠之后，竟然会比世界最高峰珠穆朗玛峰还要高，他们被指数的力量与一种大气的美震撼，将会对指数留下更深的印象.

再比如，数学中有一个非常著名且实用的不等式“真分数型不等式”，其形式为>（a，b，m∈R*，a（a，b，m∈R*，a

命题逻辑一章的知识对学生的逻辑思维具有重要的提升作用，经过相关知识的学习，学生能够更有条理地应对一些数学证明，但是这一章节的教学却具有较大难度，因为其中涉及了很多诸如“充分条件”“必要条件”这样重要但抽象的术语，学生容易混淆，将证明方向搞反. 这样的问题，教师也可以通过情境设计来帮助学生理解和记忆，比如，教师可以借助电路的知识帮助学生形象地理解有关内容. 如图2所示，电路状态和条件可以建立对应关系.

根据学生的生活环境和认知水平为他们创设合适的问题情境能让学生将抽象的数学知识和生动的生活经验结合起来，帮助学生发现数学的灵动美.

[?]鼓励创新，让学生自己创造美

所谓“授之以鱼不如授之以渔”，虽然教师可以帮助学生发现数学的美，但是如果仅仅满足这种状况，教育的价值就还没有被完全发挥出来，教师还应该在引导学生欣赏数学之美的同时，教会学生如何去创造美，适当地给学生以鼓励.

举例说明，在讲授三角函数相关内容之后笔者曾经出过这么一道例题：试证明等式=. 这样的等式证明一般的做法便是从左向右或者从右向左，通过直接计算得到相等来证明，但其实，它还有很多其他的解决方法，笔者有一位学生在解决这一问题的时候就在鼓励下采用了新方法：易知=，由这个等式根据合分比定理可知==，这就是学生在欣赏美的过程中逐渐培养起的创造美的能力.

数学本就是一门充满着美感的学科，我们不必也不应该将其变得过于严肃板正，而应该引领学生去发现美，去欣赏美，最终创造美，帮助学生学习数学知识，培养数学能力，让学习数学变得既有趣又轻松.

参考文献：

[1]  黄燕玲，喻平. 对数学理解的再认识[J]. 数学教育学报，2002（03）：40.

[2]  黄梅，黄希庭. 知识的加工阶段与教学条件[J]. 教育研究，2015（07）：108-115.