对一个不等式推广的纠正和拓展
2019-09-12 02:09:28陕西省岐山县蔡家坡高级中学722405公宽让
中学数学研究(广东) 2019年15期
陕西省岐山县蔡家坡高级中学(722405) 公宽让
1.问题
《数学通报》2018年第5期问题2421[1]如下:
已知a,b,c∈ℝ+,且a+b+c=3,求证:
文[2]对问题2421的推广如下:
(1)设a1,a2,...,an(n≥3)是非负实数,且满足则
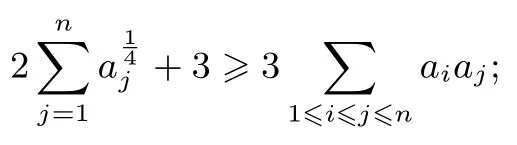
(2)设a1,a2,...,an(n≥3)是非负实数,且满足则
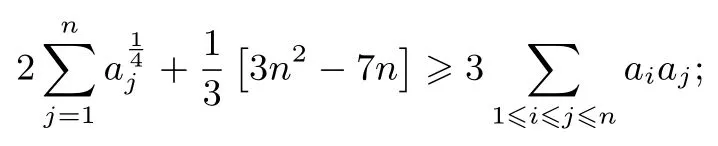
(3)设a1,a2,...,an(n≥3)是非负实数,且满足则对任意正整数k,有
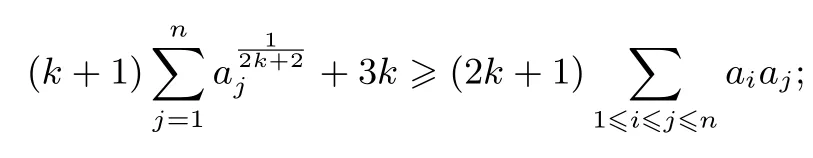
(4)设a1,a2,...,an(n≥3)是非负实数,且满足则对任意正整数k,有
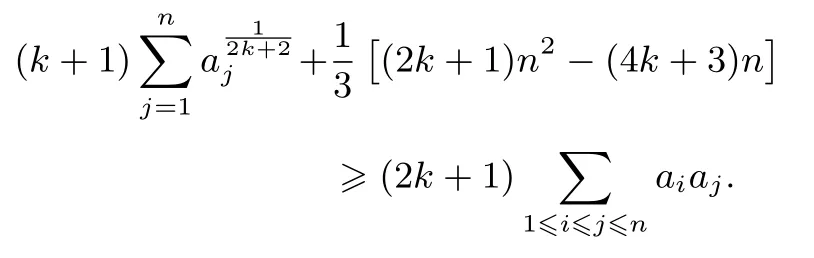
笔者发现,上述(2)、(4)有问题.当n=3时,(2)中的不等式为不是问题2421;当k=1,n=3时,(4)中的不等式也为不是问题2421.可见,文[2]中的(2)、(4)不是问题2421的推广.
2.纠正
经笔者探究,对文[2]中(2)、(4)的错误分别纠正如下.
定理1设a1,a2,...,an(n≥3)是非负实数,且满足则
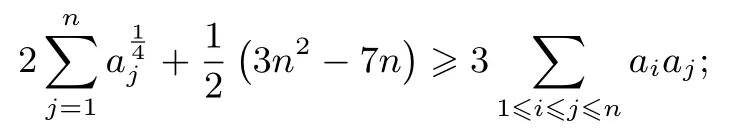
证明由均值不等式,有
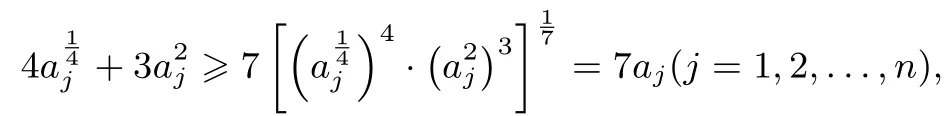
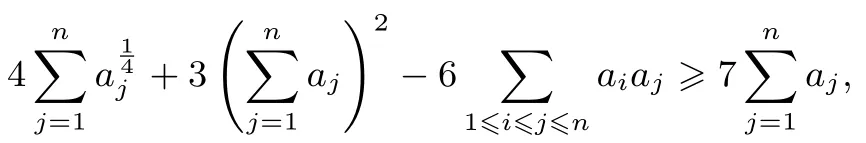
定理2设a1,a2,...,an(n≥3)是非负实数,且满足则对任意正整数k,有
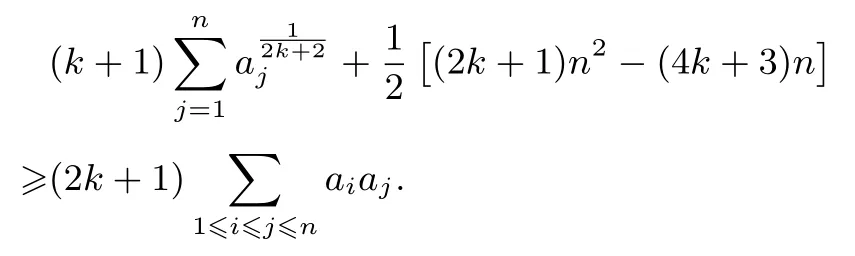
证明由均值不等式,对j=1,2,...,n有
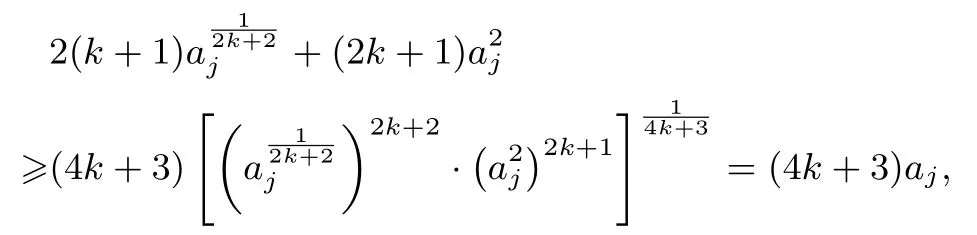
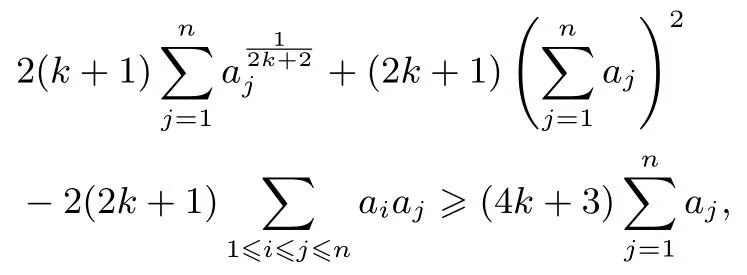
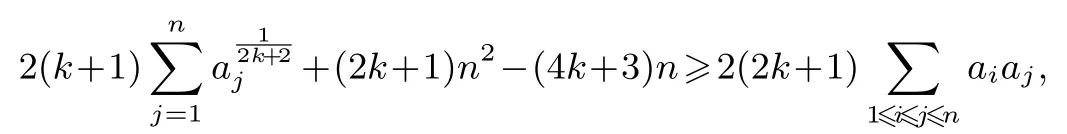
3.拓展
文[2]及上面的研究只是对问题2421按其形式(根指数为大于等于4的偶数)作了推广,其实,问题2421还可以拓展到更一般的情形.
(1)问题2421的拓展
定理3设a,b,c∈ℝ+,且满足a+b+c=3,则对任意正整数k,有
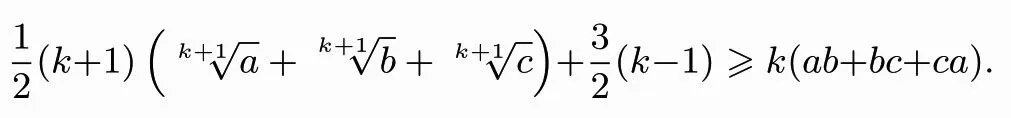
证明由均值不等式有,
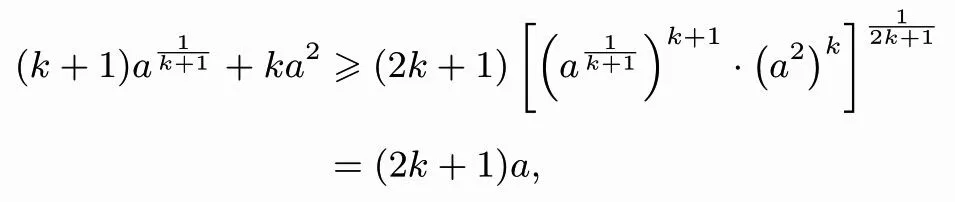
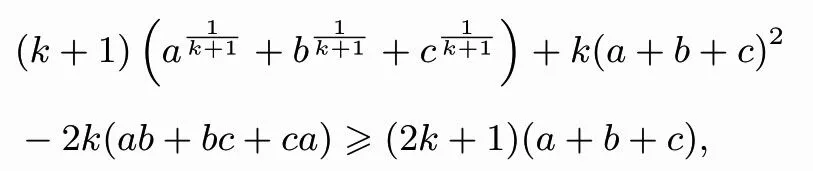
(2)问题2421拓展的推广
定理4设a1,a2,...,an(n≥3)是非负实数,且满足则对任意正整数k,有
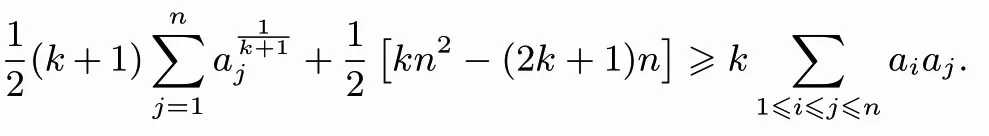
证明由均值不等式,有
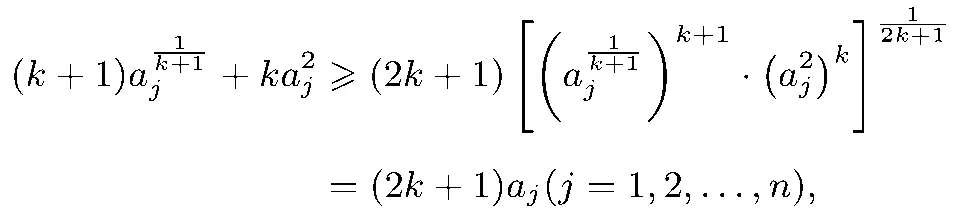
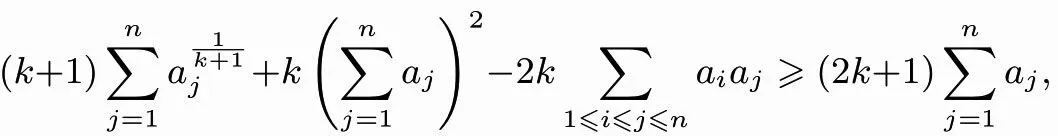
猜你喜欢
中学生数理化·七年级数学人教版(2023年3期)2023-03-21 00:45:16
中等数学(2019年8期)2019-11-25 01:38:14
中学数学研究(广东)(2018年13期)2018-08-11 06:18:42
中学生数理化·七年级数学人教版(2018年3期)2018-05-30 06:58:13
中等数学(2018年12期)2018-02-16 07:48:42
中学生数理化·中考版(2017年3期)2017-11-09 02:07:30
中学生数理化·七年级数学人教版(2016年2期)2016-05-30 21:20:57
高中生学习·高三版(2016年1期)2016-05-30 05:45:06
中学生数理化(高中版.高二数学)(2016年4期)2016-03-01 03:46:20
山西大同大学学报(自然科学版)(2016年6期)2016-01-30 08:29:14

