几个n元不等式

四川省成都实验外国语学校(611130) 宿晓阳

张景中院士在文[1]中指出：“推广是数学研究中极其重要的手段之一，数学自身的发展在很大程度上依赖于推广.数学家总是在已有知识的基础上，向未知的领域扩展，从实际的概念及问题推广出各种各样的新概念、新问题.”推广是研究数学的重要方法，也是数学研究性学习的重要方法，推广可以把问题一般化，从而实现从“一个题”到“一类题”的认知内化.推广可以培养学生的问题意识、探究意识和创新意识.本文尝试将一些朴实且平凡的三元不等式进行推广，得到了一些精致、有趣的n元不等式.供参考与欣赏.同时为我们的英才教育提供一点新鲜血液!

命题1设ai(i=1,2...,n)是正实数，n≥3，S=

证明由均值不等式和柯西不等式，有

上述n个不等式相加，即得

注此题是文[2]中的如下不等式的推广：

命题2设ai(i=1,2...,n)是正实数，n≥2，则

证明由柯西不等式和均值不等式，有

注此题是如下不等式的推广：

(《数学教学》2018年第6期问题与解答1032)设a,b,c是正实数„求证：

命题3设ai(i=1,2...,n)是正实数，n≥3，则

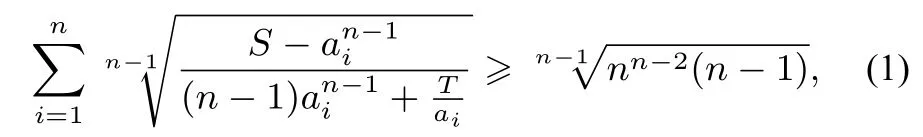
证明由均值不等式，有所以欲证不等式(1)，只需证

又由均值不等式，有

注此题是文[3]中的如下不等式的推广：

命题4设ai(i=1,2...,n)是正实数，n≥3，则

证明易知不等式(3)

注此题是如下的2006年罗马尼亚数学奥林匹克试题的推广：

命题5设ai(i=1,2...,n)是正实数，n≥3，则

证明由均值不等式，有

两边同除以n，即得不等式(4)成立.

注此题是如下的2019年罗马尼亚国家数学奥林匹克试题的推广：

命题6设ai(i=1,2...,n)是正实数，n≥3，则

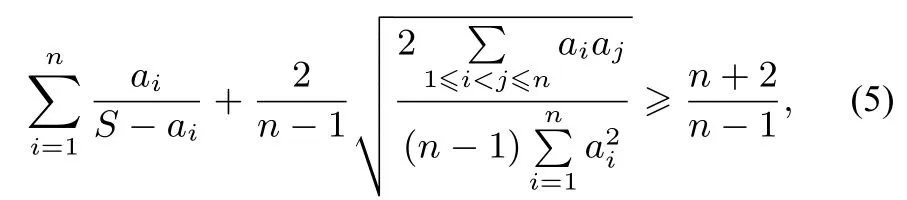
证明由柯西不等式即易知

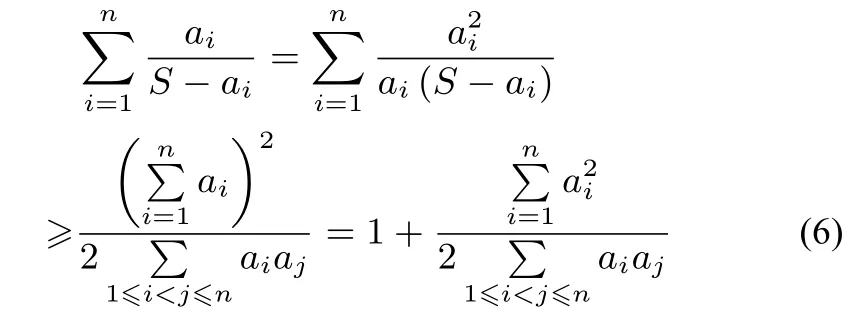
于是不等式(6)和均值不等式即得

即不等式(5)成立.

注此题是如下的2011年西班牙数学奥林匹克试题的推广：设a,b,c是正实数，求证：

命题7设ai(i=1,2...,n)是正实数，n≥3，则

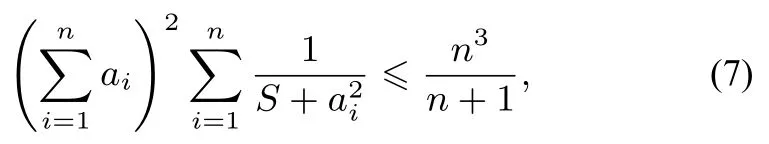
证明由于不等式(7)的对称性，不妨设由柯西不等式设则

即不等式(7)成立.

注此题是如下的《中等数学》2017年第6期奥林匹克问题与解答高531的推广：设正数a,b,c满足a+b+c=3，求证：其中∑表示三元循环和.