妙用韦达定理解决圆锥曲线中向量共线问题

湖南省长沙一中(410005) 赵意扬

向量与圆锥曲线结合的问题，其形式包括单一共线型和混合共线型.解决这类问题的关键是韦达定理的使用，看似简单的题为什么计算起来也不那么简单呢?下面就来谈一谈：韦达定理可以“这样”用.

例1已知抛物线C:y2=4x，已知点F1(-1,0)、F2(1,0)，过F1作直线交曲线C于两个不同的点P、Q两点，设若λ∈[2,3]，求的取值范围.

解析设l:x=ty-1，P(x1,y1)，Q(x2,y2)，联立得到y2-4ty+4=0，Δ=16t2-16＞0，则t2＞1，又所以构造两根之和与两根之积得

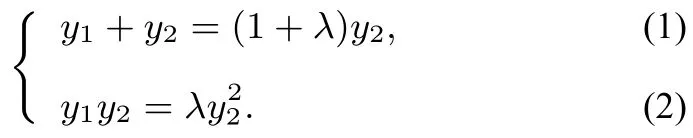
(1)2/(2)得则所以

方法总结1若能得到y1=λy2，则构造出两根之和与两根之积得到消去y2得到再利用韦达定理得于是得到若能得到x1=λx2，也同样处理.

例2已知椭圆的两个焦点分别为F1(-c,0)、F2(c,0)(c＞0)，过点E(3c,0)的直线与椭圆相交与A,B两点，且F1A//F2B，|F1A|=2|F2B|，求直线AB的斜率.

解析1由椭圆的对称性，延长AF1交椭圆于C，则设lAC:x=ty-c，A(x1,y1)，C(x2,y2)，联立

整理得(3+2t2)y2-4tcy-4c2=0，因为F1A//F2B，|F1A|=2|F2B|，所以则有故

即

解析2设A(x1,y1)，B(x2,y2)，因为F1A//F2B，|F1A|=2|F2B|，所以即或

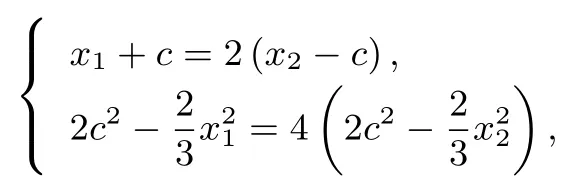
例3已知抛物线C:y2=4x，过抛物线焦点F的直线交C于A,B两点，交准线l于点M，已知求λ1+λ2的值.

解析1设直线AB的方程为：x=my+1(m0).

设A(x1,y1)，B(x2,y2)，又联立方程组消去x得：y2-4my-4=0，Δ=(-4m)2+16＞0，故

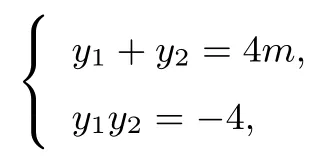
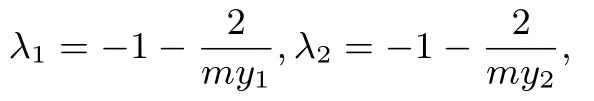
所以

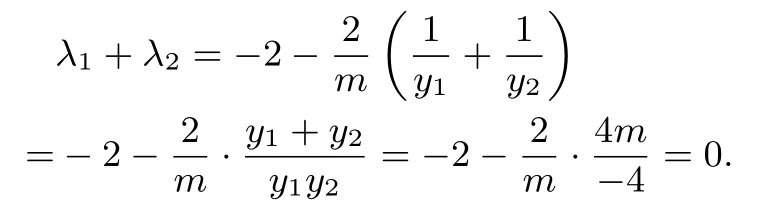
解析2由已知得λ1·λ2＜0.则：

过点A,B分别作准线l的垂线，垂足分别为A1，B1，则有：

方法总结2若则可以用A,B的横坐标x1,x2或纵坐标y1,y2来表示λ1,λ2，当λ1,λ2满足一定的关系时，进一步用韦达定理作整体代换.

例4已知双曲线过点P(0,4)的直线l交双曲线C于A,B两点，交x轴于Q点(Q点与C的顶点不重合)，当且时，求Q点的坐标.

解析1由题意知直线l的斜率k存在且不等于零.设l的方程：y=kx+4，A(x1,y1)，B(x2,y2)，则因为所以λ2所以-4=λ1y1=λ2y2，所以所以即3(y1+y2)=2y1y2，将y=kx+4代入得因为3-k20，否则l与渐近线平行.所以y1+y2=所以所以k=±2，所以Q(±2,0).

图1

解析2由题意知直线l得斜率k存在且不等于零，设l的方程：y=kx+4，A(x1,y1)，B(x2,y2)，则因为所以所以同理即

解析3由题意知直线l的斜率k存在且不等于零.设l的方程：y=kx+4，A(x1,y1)，B(x2,y2)，则因为所以所以

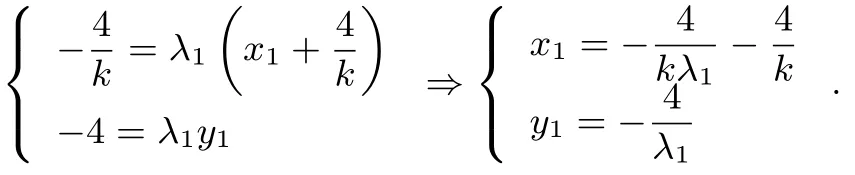
因为A(x1,y1)在双曲线C上，所以1=0，所以所以同理有：若16-k2=0，则直线l过顶点，不合题意所以16-k20.所以λ1,λ2是二次方程的两根.所以所以k2=4，此时Δ＞0，所以k=±2，所以所求Q的坐标为(±2,0).

解析4由题意知直线l的斜率k存在且不等于零.设l的方程y=kx+4，A(x1,y1)，B(x2,y2)，则因为所以Q分的比为λ1.由向量公式得

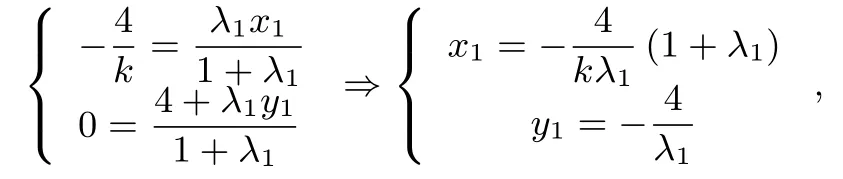
下同解法三.

例5已知过抛物线y2=2px(p＞0)的焦点，斜率为的直线交抛物线于A(x1,y2)，B(x2,y2)(x1＜x2)两点，且|AB|=9.

(1)求该抛物线的方程;

解析(1)直线AB的方程是与y2=2px联立，从而有4x2-5px+p2=0，所以由抛物线定义得|AB|=x1+x2+p=9，所以p=4，抛物线方程为y2=8x.

(2)由p=4，4x2-5px+p2=0化简得x2-5x+4=0，从而从而设即即(2λ-1)2=4λ+1，解得λ=0或λ=2.

方法总结3直线与圆锥曲线相交于A,B两点，若点M满足用A,B的坐标来表示M，如果M在曲线上，则将M的坐标代入曲线方程，如果M没有在曲线上，则必须将M的坐标表达式构造成曲线方程的形式进行处理.

例6设动点P满足其中M、N 是椭圆上的点，直线OM与ON的斜率之积为求动点P的轨迹.

解析设P(x,y)，M(x1,y1)，N(x2,y2)，则由得(x,y)=(x1,y1)+2(x2,y2)=(x1+2x2,y1+2y2)，即x=x1+2x2，y=y1+2y2.因为点M、N在椭圆x2+2y2=4上，所以故

设kOM,kON分别为直线OM,ON的斜率，由题设条件知因此x1x2+2y1y2=0，所以x2+2y2=20.

例7已知两定点满足条件的点P的轨迹是曲线E，直线y=kx-1与曲线E交于A,B两点，如果且曲线E上存在点C，使求m的值和△ABC的面积S.

图2

解析由双曲线的定义可知，曲线E是以为焦点的双曲线的左支，且易知b=1，故曲线E的方程为x2-y2=1(x＜0)设A(x1,y1),B(x2,y2)，由题意建立方程组

消去y，得(1-k2)x2+2kx-2=0.又已知直线与双曲线左支交于两点A,B，有