2019年全国联赛福建省预赛一道解析几何试题的推广*

广东省华南师范大学附属中学汕尾学校(516600) 刘光明

解析几何问题承载着逻辑推理及数学运算等数学素养，重视类比思想在圆锥曲线中的运用有利于培养学生的创新思维和激发学生探索问题的欲望.本文对2019年全国联赛福建省预赛第12题解析几何试题进行探究，发现了圆锥曲线中的一组优美性质，与读者分享.

1.试题呈现与解答

试题(2019年全国高中数学联赛福建赛区预赛试题卷第12题)已知F为椭圆的右焦点，点P为直线x=4上动点，过点P作椭圆C的切线PA、PB，A、B为切点.

(1)求证：A、F、B三点共线;

(2)求△PAB面积的最小值.

图1

试题分析(1)证明：如图1，由题意F(1,0)，设P(4,t)，A(x1,y1)，B(x2,y2)，则切线PA方程为切线PB方程为又切线PA、PB都经过点P，则因此直线AB方程为即3(x-1)+yt=0，故直线AB恒过定点F(1,0)，于是A、F、B三点共线.

(2)由消去x可得(t2+12)y2-6ty-27=0，则

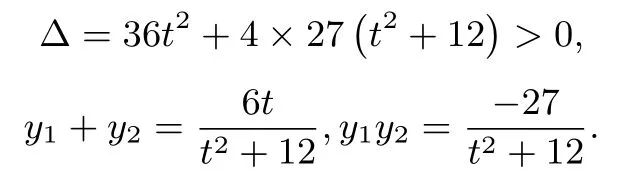
故

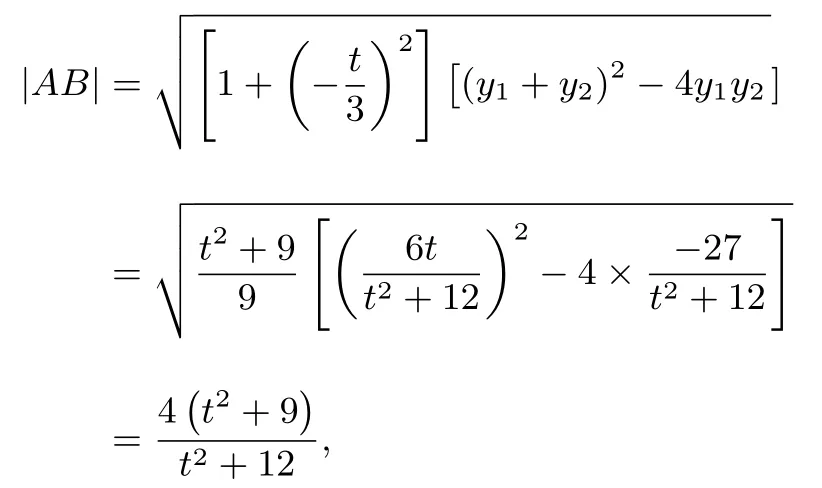
因此函数f(λ)在区间[3,+∞)上单调递增，于是fmin(λ)=故△PAB面积最小值为

点评该题以考查解析几何的基础知识、思想方法和能力素质综合立意，以三点共线、三角形面积为切入点，考查定点问题和弦长问题.在平和中见新奇，沉稳中见活力，较好地考查了圆锥曲线相关知识，又具有很好的拓展性与延伸性.

2.横纵探究，揭示本质

通过不同角度、不同层次的探索、联想、类比发现新问题，充分挖掘解析几何试题，才能揭示数学本质，进一步培养数学抽象素养，提升解析几何的魅力.经过对试题中定直线与定点之间的特殊位置关系，自然让人联想到椭圆中的一般情况，经过几何画板直观演示(如图2示)和严谨代数推理得到结论1.

结论1已知椭圆Γ:点P为直线x=t(|t|＞a)上动点，过点P作椭圆Γ的切线PA、PB，A、B为切点，则直线AB恒过点

证明设P(t,m)，A(x1,y1)，B(x2,y2)，则切线PA方程为

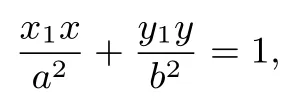
切线PB方程为

又切线PA、PB都经过点P，则

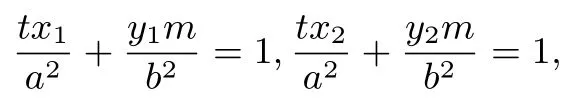
因此直线AB方程为

即b2(xt-a2)+a2my=0，故直线AB恒过定点

图2

当然，在研究有心二次曲线问题中，经常采取类比的思想，椭圆中有结论1，双曲线经过探究，也有类似的性质，见结论2所述.

结论2已知双曲线Γ:点P为直线x=t(0＜|t|＜a)上动点，过点P作双曲线Γ的切线PA、PB，A、B为切点，则直线AB恒过点

结论2的证明可以类比结论1的证明过程得到，在此不作赘述.如果进一步在抛物线中探究，也可以得到一个优美结论，详细表述和论证见结论3.

结论3已知抛物线Γ:x2=2py(p＞0)，点P为直线y=-t(t＞0)上动点，过点P作抛物线Γ的切线PA、PB，A、B为切点，则直线AB恒过点(0,t).

证明设P(m,-t)，A(x1,y1)，B(x2,y2)，又则切线PA方程为切线PB方程为又切线PA、PB都经过点P，则因此直线AB方程为即p(y-t)-mx=0，因此直线AB恒过点(0,t).

无独有偶，2019年全国3卷理科数学第21题解析几何试题就是结论3的一个特例，具体试题摘抄如下：

高考真题(2019年全国3卷理科数学第21题节选(1))已知曲线为直线上的动点，过点D作C的切线，切点分别A,B，证明直线AB过定点.

对称美是数学美的一种重要呈现，数学命题也因逆向思考而更加完美.对于结论1、结论2、结论3，从逆向探究得到了结论4、结论5及结论6.

3.逆向探究，呈现数学美

结论4已知椭圆过点Q(t,0)(0＜|t|＜a)的直线l与椭圆Γ相交于A、B两点，过A、B两点分别作椭圆Γ的两条切线l1,l2，则直线l1与直线l2的交点P恒在直线上.

证明(i)当直线l的斜率存在时，不妨设斜率为k，设A(x1,y1)，B(x2,y2)，x1x2，则直线l的方程为y=kx-kt，又直线l1方程为

直线l2方程为

由(1)×y2-(2)×y1可得

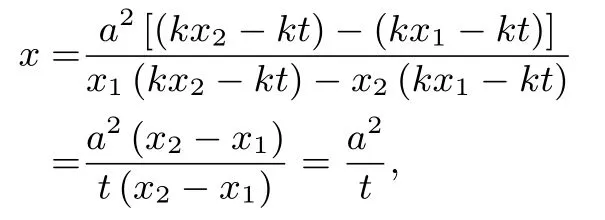
此时直线l1与直线l2的交点P恒在直线上.

(ii)当直线l的斜率不存在时，直线l的方程为x=t，根据椭圆的对称性可知此时直线l1与直线l2的交点P必在x轴上，不妨设P(x0,0)，由可得不妨设A点在x轴上方，则则

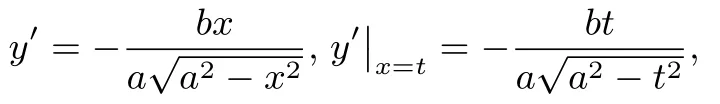
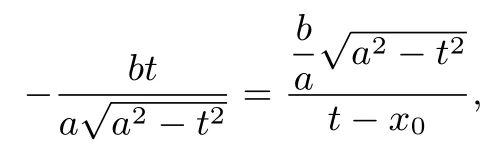
-t(t-x0)=a2-t2,于是也在直线上，综上所述，直线l1与直线l2的交点P恒在直线上.

结论5已知双曲线(a,b＞0)，过点的直线l与双曲线Γ相交于A、B两点，过A、B两点分别作双曲线Γ的两条切线l1,l2，则直线l1与直线l2的交点P恒在直线x=t上.

结论5的证明，可以类比结论4的证明得到，感兴趣的可以模仿着去推导.

结论6过点Q(0,t)(t＞0)的直线l抛物线Γ:x2=2py(p＞0)相交于A、B两点，过A、B两点分别作抛物线Γ的两条切线l1,l2，则直线l1与直线l2的交点P恒在直线y=-t上.

证明设A(x1,y1)，B(x2,y2)，由x2=2py可得则切线l1方程为

切线l2方程为

由(∗)·x2-(∗∗)·x1得

又x1x2,故由题意可知直线l的斜率存在，不妨设为k，则直线l的方程为y=kx+t，由

消去y可得x2-2pkx-2pt=0，所以x1x2=-2pt，因此

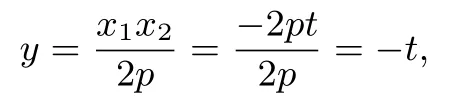
即直线l1与直线l2的交点P恒在直线y=-t上.

4.面积问题的推广

结论7已知椭圆点P为直线上动点，过点P作椭圆Γ的切线PA、PB，A、B为切点，则△PAB的面积最小值为

证明设由结论1可知直线AB的方程为即b2x+cty-b2c=0，故点P到直线AB的距离

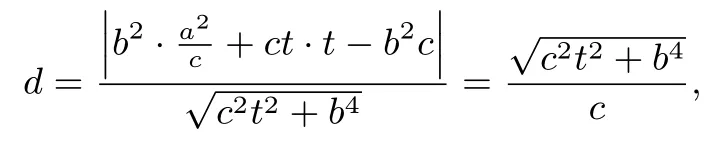
由

消去x可得

又Δ＞0，则

化简整理可得

所以

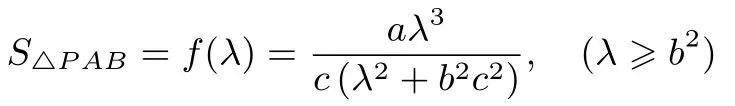
于是

函数f(λ)在区间[b2,+∞)上单调递增，因此

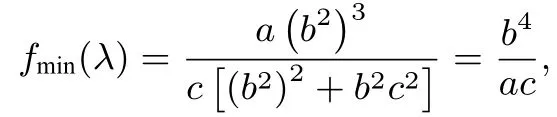
结论8已知椭圆点P为直线上动点，过点P作椭圆Γ的切线PA、PB，A、B为切点，则△PAB的面积最小值为

结论8的证明，感兴趣的读者可以参考结论7证明过程进行，在此不作赘述.

敢于猜想，善于思考，严谨求实，方能不断提高数学教师的实践能力和专业素养，提升创新意识.圆锥曲线内容丰富多彩，活力四射，精心雕琢、用心推理定能让其魅力绽放，绚丽夺目.