巧用变式化解疑难*

广东省广州市第十六中学(510080) 程延清

在新课程的教育改革中，以及新高考背景下，解题能力的培养不仅体现在数学思维的提升上，从中折射出的多种综合思维能力，更加契合新课程改革中对学生综合素养的要求.加强对数学疑难问题处理能力的培养可以有效提升数学思维能力，在寻找解题途径与思路的过程中，也能间接地提升个体对事物的综合处理能力，对个人综合素养的塑造有重要影响和作用.因此，提高数学疑难问题的处理能力一方面可以帮助数学思维的发展，对个人综合能力的发展亦大有裨益，研究数学疑难问题的解题途径和策略有其必要性和有效性.本文将通过一道高考数学模拟题解题途径和策略的探讨，剖析和优化数学疑难问题的求解策略和方法.

一、疑难问题剖析

问题已知f(x)=e2x-ax2，a∈ℝ，若f(x)在(0,+∞)上存在极大值M，证明

(本题出自2019年广州市普通高中毕业班综合测试(一)(理科数学)第21题)

解题思路遇阻原因剖析

函数的相关概念较为抽象和难以理解，对极值点、极值等概念掌握不到位也是解题思路遇阻的原因之一，由于存在概念上的理解性缺失，不能有效地从最基本的概念和方法入手突破解题思维的束缚，对函数解题方法的灵活性和函数思维的复杂性掌握不够，影响对解题思维的方向性把控.从而无法熟练的运用转化化归和分类讨论等数学思想方法突破解题思维的限制.

二、回归基础，破解难点

如何破解此题的思维难点，突破思维瓶颈是成功解决本题的关键，从数学基本概念和基本方法入手，通过题意剖析，明确需加强对函数单调性、极值等基本概念的理解，以及在深刻理解的基础上，熟练掌握利用导数研究函数的单调性、极值的基本方法.利用转化化归的数学思想方法，通过变式分步突破本题的疑难点，冲破解题思维的限制和束缚.本题的“主问题”是不等式的证明，但如果直接从“主问题”入手，由于极大值M无法直接解出以及a的不确定性，则难以直接证明不等式成立，思维也必然受阻.鉴于此，我们可以合理的转化本题的“主问题”，把问题的关注点聚焦在题设条件上，进行变式，把问题转化为求函数的极大值，达到化难为易的目的.

三、逆向变式，分步施策

关注函数相关基本概念(极大值)和基本方法，通过思考和寻找解题途径引起认知冲突，启迪思维进行合理地转化化归，挣脱“主问题”的思维束缚，把“主问题”转化为更为单一的“辅问题”.

变式化归

变式1已知f(x)=e2x-ax2，a∈ℝ，x∈(0,+∞)，求f(x)的极大值M.

思考(1)如何求函数f(x)=e2x-ax2，a∈ℝ，x∈(0,+∞)的极大值？

(2)函数f(x)=e2x-ax2，a∈ℝ，x∈(0,+∞)是否存在极大值？

由于参数a的不确定性，引起对极大值是否存在的思考，产生分类讨论的思维意识，带着问题进行思考，促使进一步的引申和变式.

变式2若函数f(x)=e2x-ax2在(0,+∞)上存在极大值，求实数a的取值范围.

通过逆向思维，进一步转化问题，使得问题更加贴近日常思维，回归数学概念的本真.由于函数的极值与函数的单调性密切相关，因此极大值的问题本质上是要解决函数的单调性问题，从而把问题转化为研究函数的单调性问题，重新设计变式，由难入易，体现数学化归思想的本质.

变式3若函数f(x)=e2x-ax2在(0,+∞)上单调递增，求实数a的取值范围.

将“主问题”转化为熟悉的“辅问题”，进一步降低题目的难度，让题目变得更加熟悉，从而降低解题的难度.

通过对变式3的解答，容易得出a≤2e，结合函数取得极值的充要条件，可以大胆猜测当a＞2e时，函数f(x)=e2x-ax2在(0,+∞)上存在极大值.不妨取a=e2加以验证.

变式4求证：函数f(x)=e2x-e2x2在(0,+∞)上存在极大值.

将参数a的不确定性确定化，使问题进一步回归到极值的基本概念以及求极值的基本方法上来.通过变式分析，回归基础，思考最初问题的解决方案，理顺解题思路.

最后，引领解题思维，从最基础和最熟悉的题型入手，反向寻求解题途径，从而突破疑难题的思维痛点和难点，通过转化化归将问题落点在基础题型与基本方法的理解和掌握上.

四、反向解题，突破难点

变式4求证：函数f(x)=e2x-e2x2在(0,+∞)上存在极大值.

证明f′(x)=2e2x-2e2x，f′′(x)=4e2x-2e2，f′(x)在单调递增，在单调递减，且所以存在使得f′(x1)=0.当x∈(0,x1)时，f′(x)＞0，当时，f′(x)＜0，所以f(x)在x=x1处存在极大值.

变式3若函数f(x)=e2x-ax2在(0,+∞)上单调递增，求实数a的取值范围.

解函数f(x)=e2x-ax2在(0,+∞)上单调递增，等价于f′(x)=2e2x-2ax≥0在(0,+∞)恒成立，等价于在(0,+∞)恒成立，令易求gmin(x)=2e，故a≤2e.

变式2若函数f(x)=e2x-ax2在(0,+∞)上存在极大值，求实数a的取值范围.

解由变式3可知，当a≤2e时，函数f(x)=e2x-ax2在(0,+∞)上单调递增，故当a≤2e时，函数f(x)=e2x-ax2在(0,+∞)上不存在极大值，当a＞2e时，f′(x)=2e2x-2ax，f′′(x)=4e2x-2a，f′(x)在单调递增，在单调递减，且所以存在使得f′(x1)=0，且当x∈(0,x1)时，f′(x)＞0，当时，f′(x)＜0，所以f(x)在x=x1处存在极大值，故a＞2e.

变式1已知f(x)=e2x-ax2，a∈ℝ，x∈(0,+∞)，求f(x)的极大值M.

解由变式2可知，存在使得f(x)在x=x1处存在极大值，且极大值

(2019年广州市普通高中毕业班综合测试(一)(理科数学)第21题)已知f(x)=e2x-ax2，a∈ℝ，若f(x)在(0,+∞)上存在极大值M，证明

解由变式1可知，存在使得f(x)在x=x1处存在极大值且f′(x1)=2e2x1-2ax1=0，即有e2x1=ax1.因为a＞2e，所以

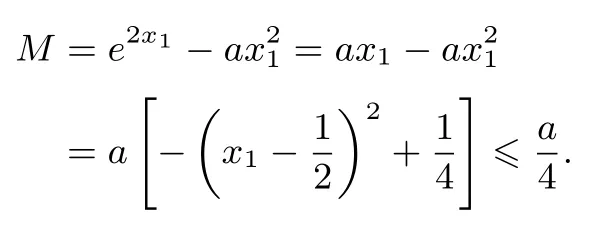
五、反思引申，强化迁移

透过解题过程的演化渗透转化化归的数学思想方法，理解和掌握转化化归的数学思想内核，通过变式破解函数难题的思维瓶颈，设计“主问题”和“辅问题”加深数学基本概念的理解和掌握.

本题最初的“主问题”是证明不等式恒成立问题，通过变式引领思维的发展，把“主问题”一步一步引向求极值以及分类讨论求参数范围等熟悉的“辅问题”上，从而逐步突破“主问题”的思维难点，化难为易，从熟悉的“辅问题”出发，抽丝剥茧，思维层次得到提高，变式设计层层递进，难度逐级降低，通过变式引申“辅问题”，回归数学概念和基础，提高破解难题的思维能力，让思维的发展过程看得见.更加真切的明白解题思维获得的来源，提升问题的转化化归能力，化繁为简，变难为易，体现数学思维的本真！