谈谈在初中数学教学中培养学生数学建模能力

吕慧

【摘要】  数学建模思维是学生重要的一种思维能力，是学生探究数学的重要途径之一，且在建模思维培养过程中促进学生数学知识内化，激发学生创新创造意识，提高学生数学分析能力以及解决问题的能力，奠定学生终身学习与发展的基础。

【关键词】  初中数学 数学建模 创新思维 逻辑思维

【中图分类号】  G633.6               【文献标识码】  A     【文章编号】  1992-7711（2019）20-134-010

学生数学能力的提高是基于解决各种数学问题场景中实现的，在具体的数学问题场景中，充分调动知识体系，运用逻辑思维推理思维、论证思维、数学抽象思维、数学运用思维进行整合加工，解决数学问题，由此，真正促进学生思维体系发展，发展学生数学能力。从科学的角度来看，数学建模是建立数学模型解决实际问题的全过程，其包括了数学模型的建立、求解、分析和检验四大步骤，可见整个过程中，数学建模将实际问题转化形象具体的数学问题模型，由此使得问题探究得其章法，问题得以创造性解决。

1.深挖教材，渗透数学建模教学

学生的数学建模能力不是一蹴而就的，其作为一种相对复杂的数学能力，是在长时的学习环境中，在教师的引导教学下而形成的。教材是教学基石，是学生根本知识的来源，甚至学生建模过程也是教材知识应用的过程。因此，教师在教学就要有意识地根据教材内容，渗透对学生数学建模思维与能力培养，利用数学建模的方式引导学生学习教材内容的同时，利用教材知识为载体，培养学生数学建模思维。

1.1阅读建模类型

问题1：我们知道我们常用的是十进制，而计算机程序使用的是二进制，即只有数码0和1，两者之间的换算过程如以下：

对于二进制（100），为（100）=1×2+0×2+1×2=4+0+1=5

对于二进制（1011），为（101）=1×2+0×2+×2+1×2=1

根据例题，将二进制换算成十进制结果为：__________

解为：9

分析：该题型重在考察学生阅读理解能力，培养学生基本的运算能力，学生通过阅读理解总结信息，探寻规律，进而在数学模型中运用数学规律。在各个数学章节中，教师都可以通过设计此类数学模型，培养学生数学能力。

2.2不等式组数学模型

问题2：某地租赁公司共有50台联合收割机，其中甲型20台，乙型30台。先将这50台联合收割机派往A、B两地区收割小麦，其中30台派往A地区，20台派往B地区。

两地区与该租赁公司商定的每天的租赁价格见下表：

每台甲型收割机的租金 每台乙型收割机的租金

A地区 1800元 1600元

B地區 1600元 1200元

问如果要使这50台联合收割机每天获得的租金最高，请你为该租赁公司提一条合理化建议。

解为：28，29，30这三个值，因此有三种方案。

分析：该题为不等式组的数学建模题型，揭示了一个本质的问题，实际上对于一些数学问题，有时不需要确定具体的数值，但可以求出或确定这一问题中某个量的变化范围，从而找到问题的突破口这一数学规律。因此在类型的数学建模过程要点中，首先建立函数关系式，由不等式的关系求出自变量的取值范围，进而求出分配方案。

2.引进生活，渗透数学建模应用

构建课堂与实际生活相联系的桥梁，促进学生知识内化。同时将生活中的问题利用数学建模去剖析其本质，可谓给学生一双慧眼，将生活看透，启发学生学以致用意识。在此过程中也增加了课堂教学的趣味性，从而极大地调动学生参与性，激发学生积极主动学习的意识。

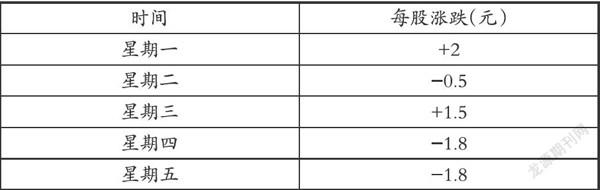
问题3：王上周五在股市以收盘价（收市时的价格）每股25元买进某公司股票1000股，在接下来的一周交易日内，小王记下该股票每日收盘价格相比前一天的涨跌情况：

根据上表回答问题：

①星期二收盘时，该股票每股多少元？

②周内该股票收盘时的最高价，最低价分别是多少？

③已知买入股票与卖出股票均需支付成交金额的千分之五的交易费。若小王在本周五以收盘价将全部股票卖出，他的收益情况如何？

解为：①26.5（元/股）;②28（元/股）;③1740（元）。

分析：该数学问题场景是学生以后生活中将接触到的投资理财的场景，具有一定的实际的意义。将其引进课堂教学中，可以培养学生对数学学习的兴趣。该案例中学生从图表、文字中搜集需要的信息，并将之转化成解决数学问题的条件，因而在数学建模过程促进学生将知识向能力转化，深化了教学的意义。在初中数学各个章节中，可以针对性搭建起与学生生活实际桥梁，重学生体验，重典例，给学生更多学习的启发。

3.自主合作，渗透数学建模迁移

倡导学生自主学习，合作学习，让学生自主思考。有学者指出，让学生发现一个问题，比让学生解决一个问题更加实际的意义。而让学生发现问题，最根本的途径就是让学生自主学习，在自主学习中，充分调用已有的知识体系，探寻知识。我们在数学教学过程中，利用数学建模思维，让学生积极探究数学问题，让学生在丰富的场景中将知识迁移内化。

问题4：为所在小区设计一个最佳的邮政投递路线

解：该数学学习活动然后学生自主合作进行，并没有标准的答案。但该数学探究活动更突显了学生数学探究的过程，突显了学生数学建模思维的时间过程。

分析：首先要教师要给学生一些活动建议，发挥教师点拨、启发的作用：按居住地成立4-6人的小组，对要研究的小区进行观察，收集必要的数据和信息（如平面图，楼的门洞的朝向，道路情况，小区的进出口位置等），分工合作完成测量方案的设计、实测、作图、计算、论证、比较、计算机文稿录入、结果介绍等。最后，得出最佳的路线之后，先不按投递要求随意地走一遍，再按设计的路线实际走一遍，测算出路程看一看相差多少？（记录数据）。在总结分享环节，我们应该更加注重学生在这个过程的体验与感悟，让学生获得真正做数学的乐趣。

在初中数学教学中培养学生数学建模能力，倡导教师在教学中深挖教材资源，丰富生活元素，再者开展学生自主实践活动，我们要实现的教学效果不仅仅是实现对学生数学建模思维的培养，更重要的是在诸多数学建模问题中，让学生发展数学学习思维，提高数学学习能力。

[ 参  考  文  献 ]

[1]齐建华.现代数学教育[M].郑州：大象出版社，2001.

[2]孙雪玉.在初中数学教学中渗透数学建模思想[J].中学教学参考，2014（34）.