日本2018年全国学力·学习状况调查测试卷（小学六年级）

◇编译/林炳雄

（编译者单位：广东深圳市罗湖区教育科学研究院）

A 卷

1.现有一根长0.4m，重60g 的铁丝。

（1）这样的 0.2m 铁丝是多少克？0.1m 铁丝是多少克？请分别作答。

（2）这样的1m 铁丝重多少克？

用□g 表示1m 铁丝的质量，用图1表示铁丝的长度和质量之间的关系。请在图中A、B、C、D、E、F 各点中选出合适点，标上 0.4m 的“0.4”，60g 的“60”和□g 的“□”。

图1

（3）求1m 铁丝质量的正确算式是（ ）。

A.60+0.6 B.60×0.4

C.60÷0.4 D.0.4÷60

2.可以用算式12÷0.8 解答的题目是（ ）。

A.1m 长的铁棒重 12kg，0.8m 长的铁棒重多少千克

B.用 0.8L 的油漆可以涂 12m2，1L 油漆可以涂多少平方米

C.红色胶带长12cm，白色胶带的长度是红色胶带的0.8 倍，求白色胶带的长度

D.把长12m 的丝带截成每段长0.8m 的小段，可以截成几段

3.比较下面两个三位整数的大小。

562 5□3

当5□3 大于562 时，□里应填什么数字？把0 到9 中符合要求的数字都写下来。

4.回答下面的问题。

（1）有 A、B 两块面积相等的地毯。

下表表示的是每块地毯的面积和坐在相应地毯上的人数。

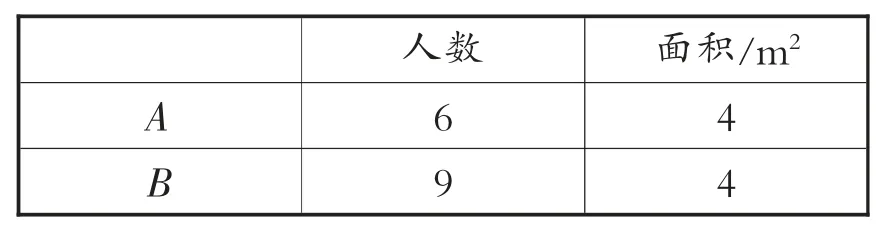
人数 面积/m2 A 6 4 B 9 4

根据上表所给的条件，从下面所给的选项中选出一个合适的答案:（ ）。

A.A 比较拥挤 B.B 比较拥挤

C.A 和 B 一样拥挤

（2）有C 和D 两块面积不同的地毯。

下表表示的是每块地毯的面积和坐在相应地毯上的人数。

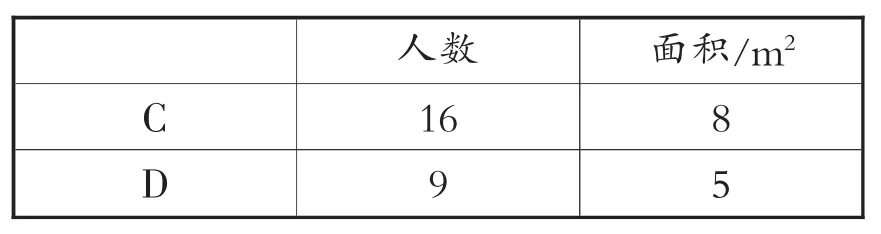
人数 面积/m2 C 16 8 D 9 5

为判断哪块地毯更拥挤，列出了下面两个算式：

C 16÷8=2

D 9÷5=1.8

根据上面的计算，请从下面所给的选项中选出一个合适的答案:（ ）。

A.因为 1m2分别坐 2 人和 1.8 人，所以，C更拥挤

B.因为 1m2分别坐 2 人和 1.8 人，所以，D 更拥挤

C.因为 1 人分别占 2m2和 1.8m2，所以，C 更拥挤

D.因为 1 人分别占 2m2和 1.8m2，所以，D 更拥挤

5.如图2，点 O 是圆心，OA、OB 是两条半径，∠a 是这两条半径的夹角。

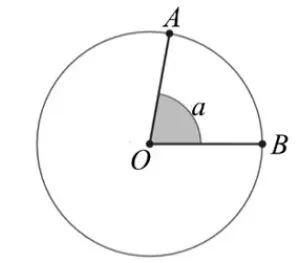
图2

如图3（1），边OA 按箭头方向旋转，夹角∠a逐渐变大。如图3（2），OA、OB 成一条直线，它们的夹角是∠b。如图3（3），它们的夹角是∠c。

图3

（1）请选择：图3中夹角∠b 的度数是（ ）。

A.0° B.90° C.180°

D.270° E.360°

（2）填空：如图4，用量角器测量图3（3）中夹角∠c，它的度数是（ ）。

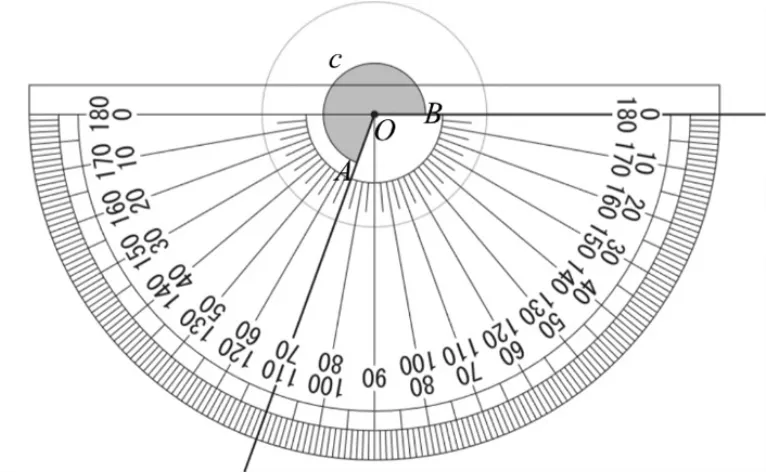
图4

6.有一张方格纸，方格的边长是1cm。上面堆叠有棱长1cm 的立方体。

现有一些立方体按如图5所示堆叠。

图5

当立方体按如图5中A、B 摆放时，其位置描述为：

请描述此时立方体C 的位置。

7.请回答以下问题。

（1）下面的选项中，求圆周率的算式是（ ）。

A.周长×半径 B.周长×直径

C.周长÷直径 D.直径÷周长

（2）一个圆的直径变为原来的2 倍，这个圆的周长是原来的（ ）倍。

A.2 B.3.14 C.4 D.6.28

8.在 A、B、C、D、E 五个地点，分别测量了同一天上午9 时到下午5 时每小时的气温。为将A地的气温与其他四地的气温作比较，制作了4 张折线统计图（如图6）。

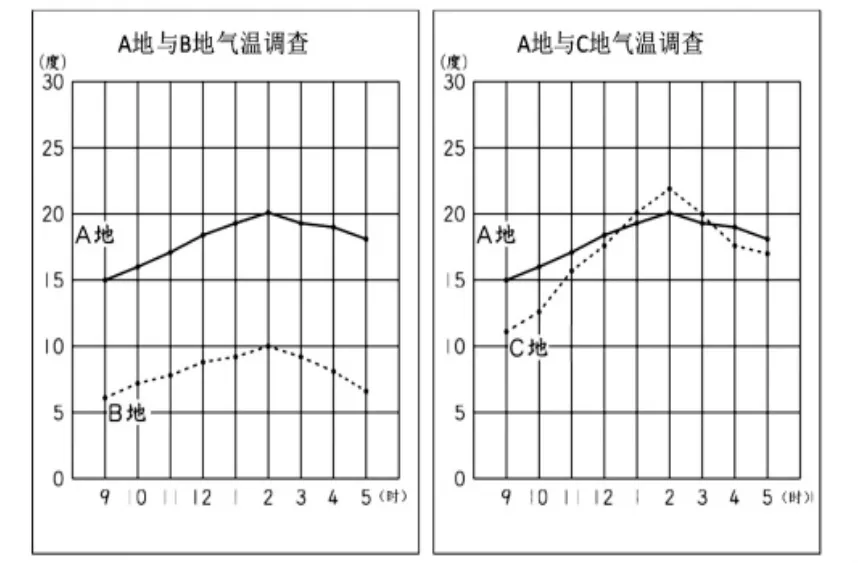
图6

观察图6，能同时满足下列两个条件的是（ ）地。

B 卷

1.在我们的身边，有很多利用图形的边与边完全重合，并且可以不断重复排列形成的图案。小明和他的朋友们对这类图案十分感兴趣。他们对此进行了研究。

下面是他们研究的由正三角形（等边三角形）组成的鳞形图案（如图7）。

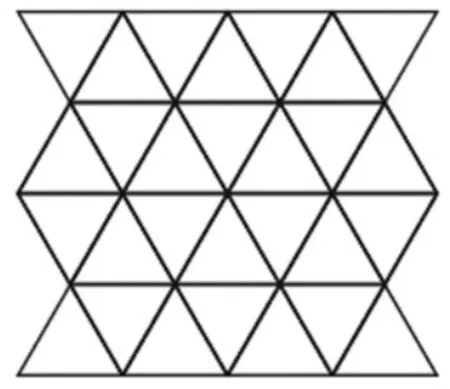
图7

小明他们在鳞形图案中描画出了各种各样的图形。

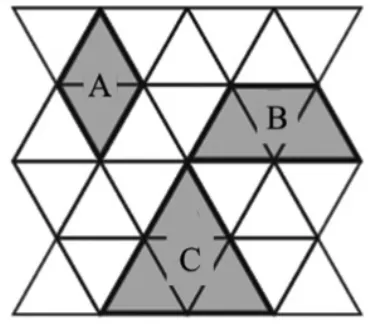
图8

小明说：由2 个正三角形可以组成菱形A。

小刚说：由3 个正三角形可以组成梯形B。

小娜说：由4 个正三角形可以组成正三角形C，那么由4 个正三角形还能不能组成别的形状呢？

（1）在上面的鳞形图案中，由4 个正三角形还能组成的图形是（ ）。

A.长方形 B.直角三角形

C.平行四边形 D.正六边形

如有困难，可以借助图7自己试着画画看。

接下来小明和他的朋友们对龟壳图案进行了研究。龟壳图案是由正六边形组成的。他们对鳞形图案和龟壳图案（如图9）做了如下描述。

图9

小明说：因为图形的边与边完全重合，没有一点缝隙，所以围绕在点A 和点B 周围的角的度数和都是360°。

小刚说：在点A 的周围有6 个正三角形的角围绕，而正三角形每个角都是60°，所以围绕在点A 周围所有角的度数和是 60°×6＝360°。

小娜说：在点B 的周围有3 个正六边形的角围绕，而正六边形每个角的度数都是120°，所以围绕在点 B 周围所有角和是 120°×3＝360°。

小明和他的朋友们还对笼目图案进行了研究。笼目图案是由正三角形和正六边形组合而成的。（如图10）

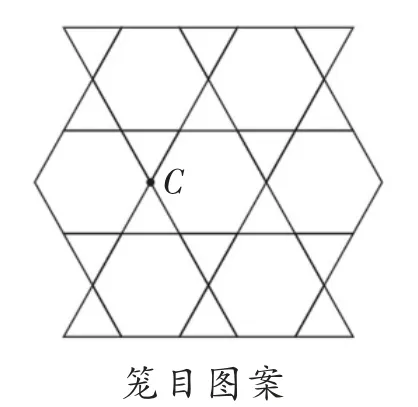
图10

（2）请写出围绕在点C 周围的图形的名称，并用算式表示这些图形每个角的度数与点C 周围所有角的度数和360°之间的关系。

2.张老师计划在一年级学生联欢会上进行投篮游戏。

首先，明确投篮游戏的规则。

接下来，制订了如下计划。

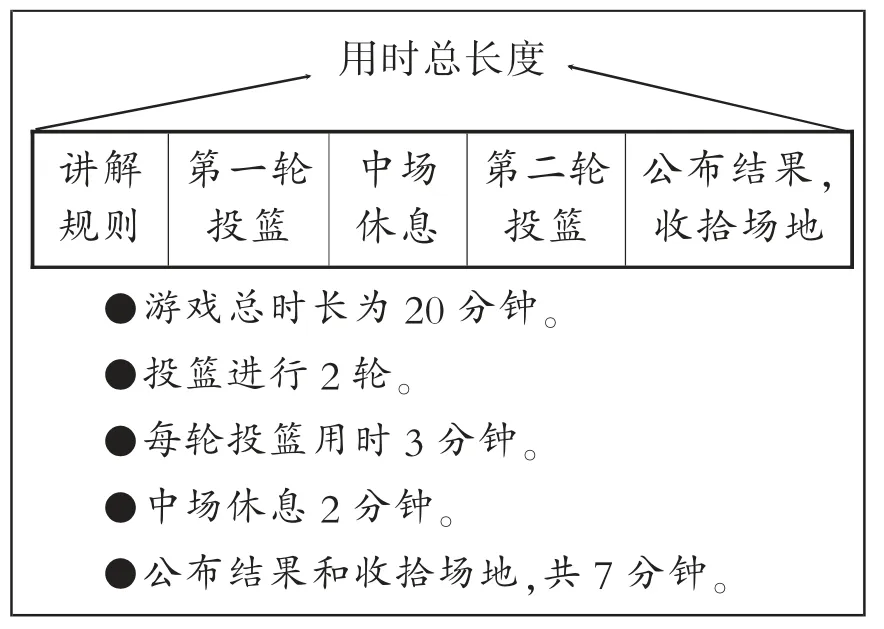
（1）在张老师的计划里，讲解规则部分可用时间为多长分钟？

每轮投篮包括投球的时间和数进球数的时间。为保证每轮投篮都在3 分钟以内，请思考投球需要多长时间。

小明说：每轮投篮的用时如下面的算式所示：投球时间+数球时间=每轮投篮用时。

设数每次进球用时2 秒。

投球时间越长，进球数也会更多，随之数进球数的用时也会越长。

因此，张老师将每轮投篮的投球时间设定为40 秒。

当投球时间为40 秒时，一轮投篮用时142秒。当投球时间延长到50 秒和60 秒时，一轮投篮的进球数分别增加到64 个和80 个。

（2）为了能让每轮投篮耗时尽量接近3 分钟，投球时间用 40 秒、50 秒、60 秒，哪个更好呢？

仍设每数一个进球所花时间为2 秒，请在下面作业纸表格的（ ）中填写正确答案。请在40 秒、50 秒、60 秒中选择正确的答案填入作业纸的[ ]中。

作业纸投球时间40 秒50 秒60 秒进球数51 个64 个80 个数进球数时间102 秒（ ）秒（ ）秒一轮游戏时间142 秒（ ）秒（ ）秒当投球时间是[ ]秒时更好。

3.芳芳的学校举行了“坚持向别人问好”和“经常读书”两个活动。学校在7月和12月对全校625 人进行了问卷调查，结果用条形图呈现，如图11。芳芳通过观察条形图做出两个笔记。

图11

雯雯和天天就芳芳做的笔记展开了讨论。

雯雯：在笔记1 中坚持问好的人多，但是在笔记2 中经常读书的人多。

天天：这是为什么呢？

芳芳：笔记1 和笔记2 是从不同的视角做出的总结。

（1）对于笔记1 和笔记 2 的结论，芳芳分别是从什么视角做出的？

关于“坚持向别人问好”活动，学校在12月分3 组分别对一二年级、三四年级和五六年级进行了问卷调查。用条形图（图12）呈现结果。

图12

芳芳:参加活动并回答问卷人数最多的是五六年级。

天天:但是，一二年级、三四年级、五六年级的总人数分别为 175 人、200 人、250 人，与参加活动的人数不一样，我们来求一下参加活动人数占总人数的比例。

一二年级、三四年级和五六年级3 个组参加“坚持向别人问好” 活动人数和各组总人数的比例关系如图13。

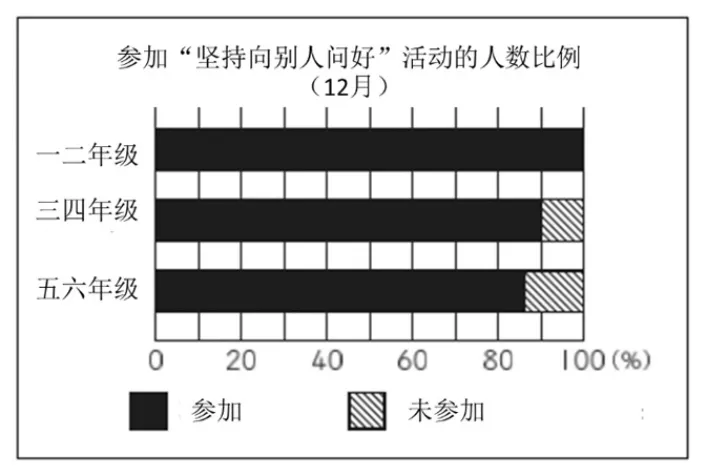
图13

（2）由图12和图13，得到以下结论：

请从下面①、②、③选项中选出正确答案填入上面的括号A，从④、⑤中选出正确答案填入上面的括号B。

4.小肖和朋友们在学习九九乘法表。

首先，我们看九九乘法表的第2 行和第3 行。

图14

下面是他们关于纵向两个数之间关系的讨论。

小肖：第 2 行的 4 和第 3 行的 6，这两个数的和是 10。6 和 9 的和是 15，8 和 12 的和是 20。它们的和都是第5 行的数。

小温:2 与 3 的和是 5，18 与 27 的和是 45。果然是第5 行的数！

小亮:根据 8 与 12 的和，18 与 27 的和与第5行的数的关系，得到下面的算式：

小肖:如小亮的想法，2＋3 等于 5，5 是被乘数。所以结果就是第5 行的数。

小温:第2 行与第3 行的数纵向相加时，都有（2+3），即被乘数为 5。所以第 2 行和第 3 行的和就是第5 行的数。

小亮:以此类推，第4 行与第5 行的数竖向相加的和就是第9 行的数。

（1）参照小肖的想法，第 4 行与第5 行纵向的两个数32、40 相加，得到如下与第9 行相关的算式，请在下面的A 框和B 框中填入算式。

下面是他们对横向连续几个数的讨论。

小肖：求横向排列的 3 个数 4、5、6 的和，4+5+6=15，结果是 15。15 是4、5、6的正中间的数 5的 3倍。

小亮：横向排列的 3 个数 18、21、24 的和是63，是正中间的数21 的3 倍。

小肖：那么，当数为横向排列的5 个的时候，又是怎样的情况呢？

小肖他们对横向排列的 5 个数 6、12、18、24、30 作了研究。

小温：横向排列的 5 个数 6、12、18、24、30，它们的和是 90，所以 90 是 18 的 5 倍。

小肖：横向排列的 5 个数 6、12、18、24、30，它们的和是90，是正中间的数18 的5 倍。

（2）请对横向连续的 7 个数 4、6、8、10、12、14、16，像小肖那样进行说明。

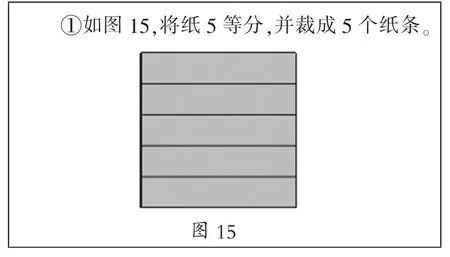
5.小樱和她的同学想在黑板的上方挂几串纸环。他们从老师那里拿到了100 张纸。每张纸可以做5 个纸环，每30 个纸环连起来为一串。

纸环串的做法

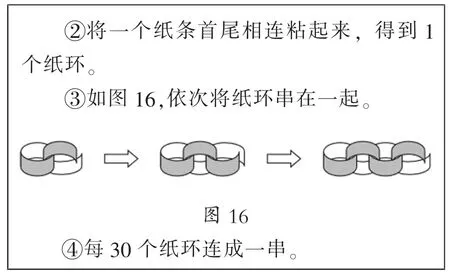
如图17所示，他们想在一块7m 长的黑板上每50cm 挂一串纸环。

图17

（1）在长7m 的黑板上，从最左端到最右端挂满纸环，如果能有100 张纸那就足够了。

下面是小宋根据上面的条件做的部分解答。

请接着小宋的解答继续证明：为什么100 张纸可以完成这项任务？

拿到的纸有红、蓝、黄、绿4 种颜色且数量相同。小樱按照图18的顺序做了一串纸环。

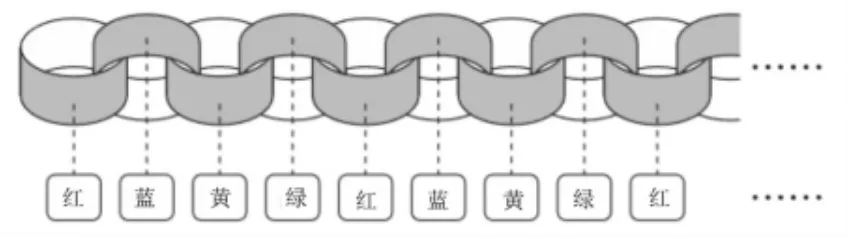
图18

（2）如图18所示，当第1 个纸环的颜色是红色时，那么第30 个纸环应该是什么颜色？

A.红 B.蓝 C.黄 D.绿