“图形与几何”试题精选

一、选择题

1.小华用6 个同样大的正方体摆成一个物体。从前面和上面看到的分别是如图1所示的图形，从右面看这个物体，看到的是（ ）。

图1

2.学校准备建一个足球场，下面三块地的面积，选（ ）比较合适。

A.100 平方分米 B.100 平方米

C.1 公顷 D.1 平方千米

3.如图2，丁丁将一些练习本摞在一起，从正面看是一个长方形，再将它们均匀地斜放，这时从正面看是一个近似的平行四边形，它们的（ ）相同。

A.形状 B.面积 C.周长

图2

4.下面的问题中，（ ）与体积有关。

A.包装一份生日礼物需要多少彩纸

B.一个玻璃球沉入装满水的杯子中，溢出多少水

C.油漆大厅里的柱子，需要多少油漆

D.给一个玻璃柜台各边装上角铁，需要多少角铁

5.小芳有2 根长分别是4 厘米、9 厘米的小棒，如果她想从下面的4 根小棒中选择1 根围成一个三角形，应该选（ ）长的。

A.3 厘米 B.5 厘米 C.8 厘米 D.14 厘米

6.图3中，甲的表面积与乙的表面积相比较，（ ）。

A.甲大 B.乙大 C.一样大 D.无法确定

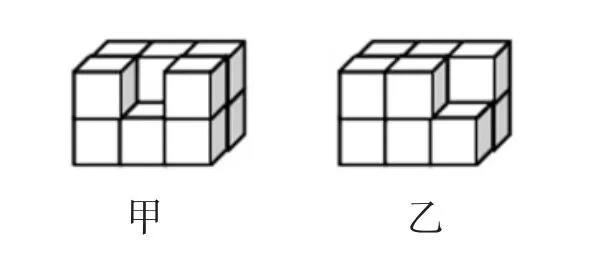
图3

7.一个长 26 厘米、宽 19 厘米、高 0.7 厘米的物体，最有可能是（ ）。

A.衣柜 B.普通手机

C.数学书 D.橡皮

8.如图4，点子图中有一个图形，有以下描述：①这是一个四边形；②这是一个平行四边形；③这是一个梯形；④这个图形有两条对称轴；⑤这个图形中有一个直角。其中正确的有（ ）。

A.①③ B.①⑤

C.①②④ D.①③⑤

图4

9.一个平行四边形相邻两条边的长分别是6 厘米、4 厘米，量得一条边上的高为5 厘米，这个平行四边形的面积是（ ）平方厘米。

A.20 B.30 C.20 或30

10.一个三角形最小的内角是55°，这个三角形一定是（ ）三角形。

A.等腰 B.锐角 C.直角 D.钝角

11.下面4 个图形中，经过折叠能围成如图5所示的正方体纸盒的是（ ）。

图5

12.张芳想把一根9 厘米长的木条截成三段围成一个三角形（每段的长度都是整厘米），有（ ）种不同的围法。

A.1 B.2 C.3 D.4

13.如图6，把一个底面半径为4cm 的圆柱，拼成一个近似的长方体，长方体的表面积比圆柱增加了40cm2，圆柱的高是（ ）cm，体积是（ ）cm3。

A.251.2 B.5 C.10 D.50.24

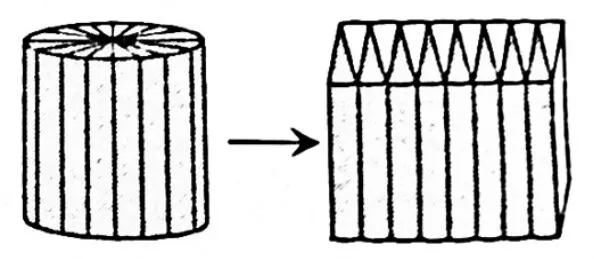
图6

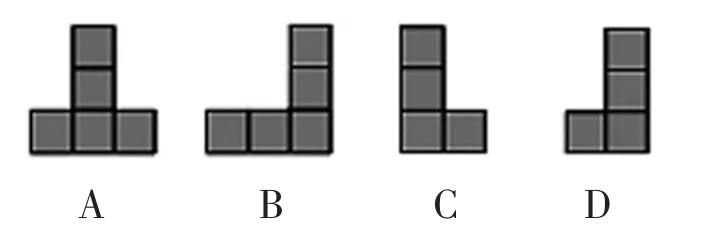
14.按图7中的描述搭成的积木，从左面看是（ ）。

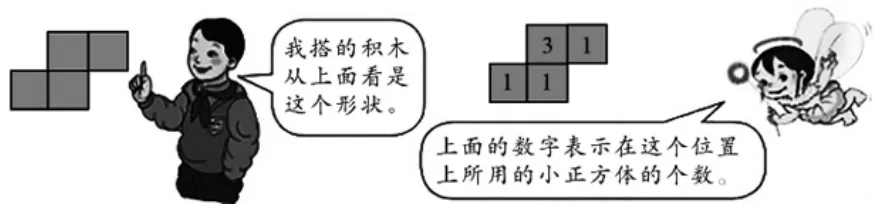
图7

15.有一张边长为4 分米的正方形纸，如果在这张纸上剪4 个最大的等圆，4 个圆的面积之和是这张纸的（ ）。

A.78.5% B.80% C.75%

16.正方形的4 个顶点都在半径为10 厘米的圆上，正方形的面积是（ ）平方厘米。

A.75 B.100 C.157 D.200

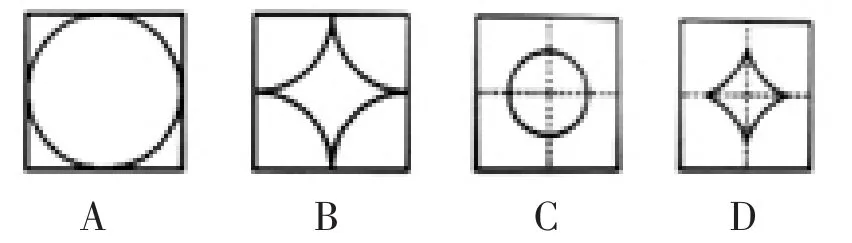
17.如图8，将一张正方形纸片沿虚线向上对折，再沿虚线向右对折，得到一个正方形，然后剪下一个角。将这张纸片展开后应该是（ ）。

图8

18.图9是某品牌汽车的标志，这个标志有（ ）条对称轴。

A.1 B.2 C.3 D.4

图9

19.如果把体积相同的两个物体，分别浸没在高度相等的甲、乙两个圆柱形水杯中，甲杯水面上升3cm，乙杯水面上升5cm，那么甲、乙两个水杯的容积之比是（ ）。

A.9∶25 B.3∶5 C.25∶9 D.5∶3

20.学校在书店北偏东30°方向 500 米处，书店在学校（ ）。

A.北偏东 30°方向 500 米处

B.南偏西 30°方向 500 米处

C.东偏北 30°方向 500 米处

D.西偏南 30°方向 500 米处

二、判断题

1.一个长方体，如果有两个相邻的面是正方形，这个长方体就是正方体。（ ）

2.如果圆柱的体积是圆锥的3 倍，那么它们一定等底等高。（ ）

3.边长是 4cm 的正方形按 2∶1 放大后的面积是32cm2。（ ）

三、填空题

1.公式推导。

我们知道，面积的大小就是含有面积单位的数量，以此类推，体积的大小就是含有（ ）的数量。我们在一个长6 厘米、宽2 厘米、高3 厘米的长方体纸盒内摆体积是1 立方厘米的小正方体木块，一行可以摆（ ）个，一层可以摆（ ）行，可以摆（ ）层，一共可以摆（ ）个木块。你发现了吗？长方体所含（ ）的数量，就是长方体的（ ），等于（ ）的乘积。

2.根据相关研究，室内景点人均活动面积低于1 平方米，室外景点人均活动面积低于0.75平方米时，就有发生踩踏事故的危险。在一个古镇景点戏台前，有一片上底是30 米、下底是50米、高是60 米的梯形室外场地，为保证安全，这片场地上最多只能容纳（ ）人同时看戏。

3.如图10，已知长方形 ABCD 中，点 A、C 的位置用数对表示分别是 A（3，8）、C（7，6）。那么点 B、D的位置用数对表示分别是：B（ ，）、D（ ，）。

图10

4.长方体容器内装有水，容器内壁底面长方形的长为15 厘米、宽为9 厘米。现在把一个圆柱和一个圆锥放入容器内，水面升高2 厘米。又知放入容器后，圆锥全部浸入水中，而圆柱则有露在水面上。如果圆柱和圆锥的底面半径、高都分别相等，那么圆柱的体积是（ ）立方厘米。

5.如图11，三个长方形的面积都是1，请用分数表示出阴影部分（三角形）的面积。

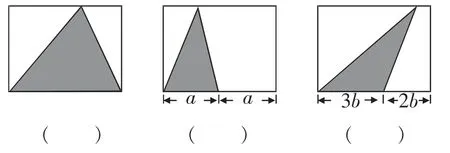
图11

6.推导圆面积公式常采用“化圆为方”“化曲为直”的转化策略。把一张圆形纸片剪开后，拼成一个宽等于半径，面积不变的长方形。这个长方形的周长是16.56cm，则这张圆形纸片的面积是（ ）cm2。

7.如图12，大圆的半径是小圆半径的2倍，阴影部分是一个正方形，面积是60 平方厘米，那么小圆的面积是（ ）平方厘米。

图12

8.如图13，平行四边形ABCD 的面积是100平方厘米，甲、乙两个三角形的面积比是5∶3，则阴影部分的面积是（ ）平方厘米。

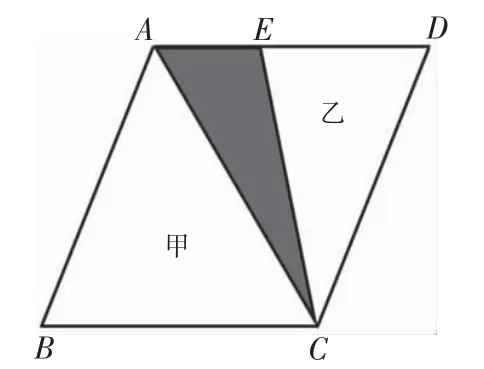
图13

9.如图14，长方形中有两个扇形，①的面积与②的面积相等。这个长方形的面积是（ ）cm2，周长是（ ）cm。

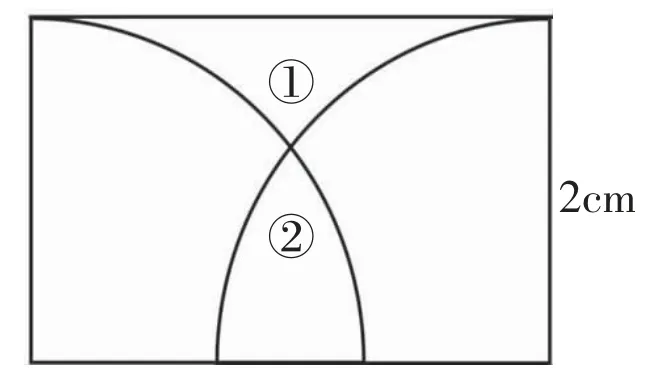
图14

10.如图15，用边长为1dm 的正方形纸板，制成一副七巧板，将它拼成“小天鹅”图案，其中阴影部分的面积为（ ）dm2。

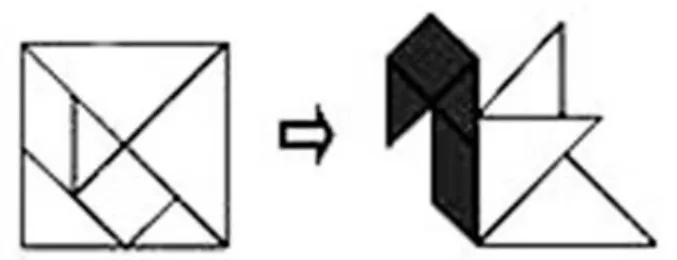
图15

四、综合应用

1.小华要买两本书，如果用纸把两本书包起来，有几种包法？哪种包法最省纸？请说明理由。（书长 17 厘米，宽 24 厘米，厚 2 厘米）

2.用一张长12 厘米、宽6 厘米的长方形纸制作一个圆柱的侧面(以桌面为底)，要求这个圆柱的容积尽可能大，但又不超过160 立方厘米。请你用自己喜欢的方式写出设计方案，并计算出这个圆柱的容积。（提示：π 取 3，接口处忽略不计）

3.在一个长 9 厘米、宽 6 厘米、高 5 厘米的长方体木块中，先锯掉一个最大的正方体，再在剩下的木块中锯掉一个最大的正方体，最后在剩下的木块中再锯掉一个最大的正方体。

（1）第一次锯掉的正方体的棱长是（ ）厘米。

（2）第二次锯掉的正方体的棱长是（ ）厘米。

（3）锯掉这三个正方体后，剩下的木块的体积是多少立方厘米？（写出解答过程）

4.一种圆柱形饮料罐，底面直径是7 厘米，高是10 厘米。将24 罐这种饮料放入一个长方体纸箱内。（如图16）这个纸箱的容积至少是多少立方厘米？做一个这样的纸箱，至少要用硬纸板多少平方厘米？（箱盖和箱底的重叠部分按1800平方厘米计算）

图16

5.如图17，把一个大正方形分成9 个相同的小方格，给图中的1 个白色小方格涂上颜色，使涂色部分成为一个轴对称图形。请用4 种不同的涂法表示。

图17

6.（1）有一个三角形，如图18所示，要把它分成三个面积相等的三角形，可用的测量工具只有一把刻度尺，请在图18中画出示意图。

（2）有一个正方形，如图19所示，要把它分成三个面积相等的四边形，且中心点O 为每个四边形的一个顶点，可用的测量工具也只有一把刻度尺，请在图19中画出示意图，并简要说明画法。

（3）有一个圆，如图20所示，要把它分成三个面积相等的扇形，测量工具只有一把刻度尺，请在图20中画出示意图，并简要说明画法。

图18

图19

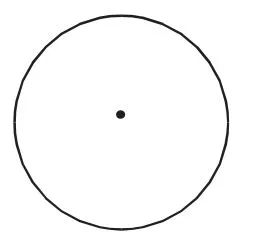
图20

五、数学作文

星期天，哲哲和瑶瑶在家玩橡皮泥。当哲哲看到手中的不规则橡皮泥时，想起了五年级所学的体积知识，他很想知道这块不规则橡皮泥的体积，你觉得他们会怎么做呢？请你以“不规则橡皮泥的体积”为题目，写一篇200 字左右的文章，要求条理清晰，结构完整。