对小学数学阅读题的分析与思考
◇ 南欲晓
近几年,温州市小学六年级毕业检测数学试卷,在原有题型的基础上增加一种题型,命名为“阅读与思考”“阅读与解答”“阅读与尝试”“读图与思考”,是以“附加题”(满分之外另计分数或等次)的形式出现的。由命名可见,此种题型是以数学阅读为背景,测试学生推理素养,这也是对纸笔测试做的新尝试。
数学阅读主要是通过一些情景故事、解题过程、数学家故事等内容,让学生在阅读中不仅关注显性内容,而且关注蕴含在阅读材料中的数学知识、方法、思想等隐性内容。数学阅读强调的不是计算的繁难,而是激发学生思维活跃,促进数学的思考和理解。
数学阅读的测评主要是检测学生通过阅读数学材料后,能否从书面材料中获取有效信息,并根据获取的信息进行加工、推理,从而解决新的问题;重要的是考查学生能否用数学的眼光观察现实世界,能否用数学的思维思考现实世界,能否用数学的语言表达现实世界。
下面以2016年温州市小学六年级教育质量综合测评数学试卷中的“阅读与思考”题为例,谈谈对数学阅读题的理解。

一、数学阅读材料简析
阅读材料(如图1)分为材料 1 与材料2。材料1 是用来判断一个分数是否可以化成有限小数,它的标准就是最简分数的分母分解成的质因数除了2和5 不含其他质因数,这是显性的知识内容。但是,这个标准是否正确?是不是所有的有限小数化成最简分数后,它的分母分解成的质因数是除了2 和5 不含其他质因数呢?这是隐性的知识内容,需要学生经过计算和推理之后才能得到。这两个知识点对于小学六年级学生来说是完全可以理解的。

图1
材料2 是纯小数与分数之间的关系。材料2 中显性的知识是:对于有限小数转化为分数,有几位小数,转化成分数的分母就是10 的几次方,分子就是小数的小数部分;对于循环小数转化为分数,循环节有几位,转化成的分数的分母就是几个连续的9,分子就是几位循环节的小数。至于为什么可以这样转化是隐性的知识,需要学生去计算与化简才能得到。
在阅读材料中用列表的方式把有限小数、循环小数与分数对应起来,便于学生理解。由此可见,在数学阅读中,学生的思维要经历从阅读材料字面意思的理解到阅读材料中各要素之间关系的明晰这样一个过程。
二、数学阅读题组简析
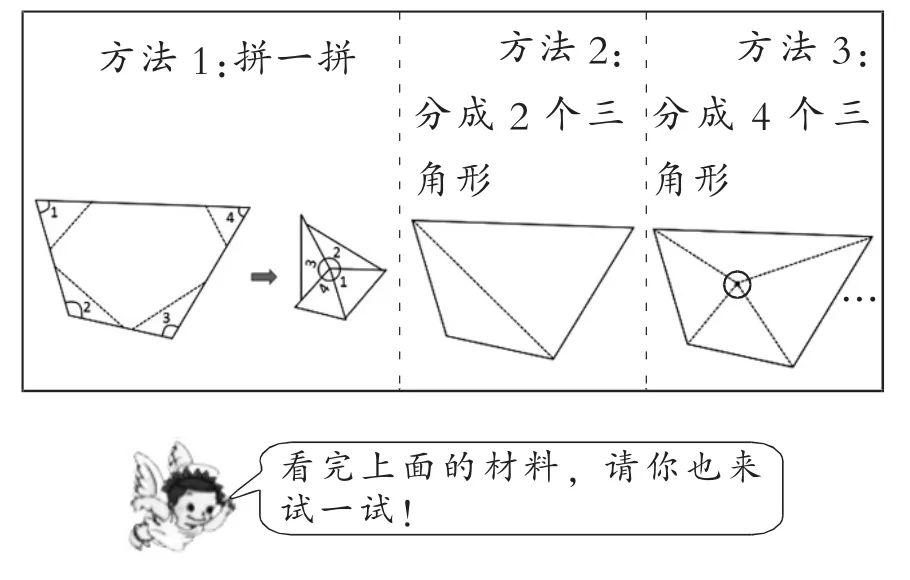
“我来判一判”(如图2),即判断所给的分数能不能化成有限小数,主要考查学生是否理解方法性内容,包括:学生能否读懂内容讲的是什么?能否在具体的例子中应用?能否将用整段描述的文字梳理成有条理的步骤?是否对方法的来源有一定的质疑能力?

图2
“我来填一填”(如图3), 要求学生不仅能发现材料2 中的循环小数和分数之间的关系,也能关注对应的有限小数和分数转化之间的联系。如,要得到首先就要发现循环节只有一位的纯小数转化为分数,它们的分母都是9,分子和循环节是相同的。在寻求联系得到规律的过程中,考查学生的推理能力,以及在面对全新的知识时是否能够重组并进一步抽象与结构化的能力。

图3
“我来试一试”(如图4),主要考查学生完成此题的思维过程。首先发现所给小数的循环节是两位,进而确定约分前的分母是99。99 的因数有1、3、9、11、33、99,根据“分母与分子之差为 9”可知,相应的分数有符合“最简分数”条件的只有最后得到的数是这是寻找规律、得出规律、应用规律的过程。在这个过程中,学生需要将一些信息按照一定的方式组织起来,准确把握其内在特征,才能明确要解决的问题,从而确定范围、不断调整,最终寻找到问题解决方案。

图4
对于“我来说一说”(如图5),许多人认为这道题有“超越课标”的嫌疑。实际上通过观察,学生不难发现“对和错”的判断主要看学生是否能够用“素材作为证据”来表达,是否能够借助“规律的适用性”做进一步的探索,是否能有根有据地思考,也就是常说的“言之有物、言之有理、言之有据”。

图5
三、数学阅读题的评价
数学阅读题考查不仅要关注学生答题情况的表现,更要关注导致这些表现背后的各种思维过程。虽然学生思维过程与理解水平难以直接检测,但是可以借助学生在作答过程中的实际表现加以判断:什么样的思维过程能够引发这样的表现?这样的表现说明学生的思维过程可能处于什么水平?因此,对于不同水平及其表现特征的刻画显得极其重要。
所以,在数学阅读题答案或标准的制定中不仅要关注答题是否正确,更要关注这个答案背后反映出的不同水平学生的思维特征和探究方式,从而判断学生理解水平的层次。
四、小学数学阅读题样题
(一)阅读与解答。
数学思想方法是数学的灵魂。转化思想作为重要的数学思想方法之一,在我们的学习生活中无处不在。如,在“曹冲称象”的故事里,把大象的质量转化为石头的质量;又如,推导平行四边形面积计算公式时,把平行四边形转化为长方形(如图6)……

图6
1.回忆一下,在以前的数学学习中,利用转化思想我们还可以将( )转化为( )来研究。
2.你还能用转化的数学思想方法来解决以下数学问题吗?
(1)一个拧紧瓶盖的瓶子里装有一些水(如图7),根据图中的数据,可以计算出瓶中水的体积占瓶子容积的( )。
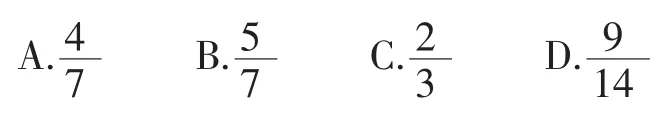

图7
(2)如图8,一张半径为4 厘米的圆形纸片在一个足够大的正方形内任意移动,这张圆形纸片不可能接触到的部分的面积是多少平方厘米?(请列式解答)
(二)阅读与尝试。
“山重水复疑无路,柳暗花明又一村……”

1.如图9,五边形的内角和是( )度。
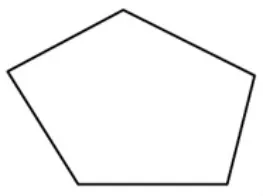
图9
2.一个多边形的内角和是1080°,它是( )边形。
3.如图10,把一个正方体木块,沿 AB、AC两条对角线削去一部分后会形成一个新的平面。在这个平面上,∠BAC 的度数是( )。
A.45° B.60° C.90° D.135°

图10
4.如图11所示,一个面积约24 平方分米的等边三角形内有一个圆形的钟面。每当整点时,钟面上都会出现一个奇妙的等边三角形阴影。阴影部分的面积是( )平方分米。
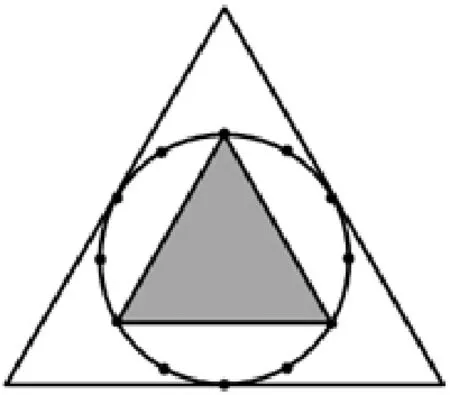
图11

