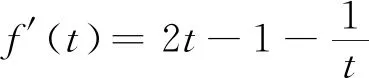错在哪里

1 安徽省安庆市第一中学

洪汪宝(邮编：246004)

(1)求椭圆C的方程；

(ⅱ)求△ABQ面积的最大值.

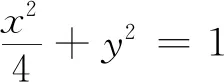
(ⅱ)设A(x1,y1),B(x2,y2)，

得(4k2+1)x2+8kmx+4m2-16=0，

所以△=(8km)2-4×(4k2+1)(4m2-16)=16(16k2+4-m2)>0.

当且仅当m2=16k2+4-m2，即m2=8k2+2，符合△>0，△ABQ面积的最大值为12.

解答错了！错在哪里？

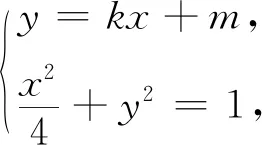
得(4k2+1)x2+8kmx+4m2-4=0，其判别式

△′=(8km)2-4×(4k2+1)(4m2-4)=16(4k2+1-m2)=-16(4k2+1)<0，

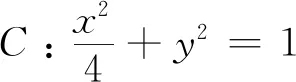
那么△ABQ面积的最大值到底怎么求呢？

正解同前得

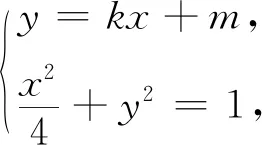
△′=(8km)2-4×(4k2+1)(4m2-4)=16(4k2+1-m2)≥0，得m2≤4k2+1，

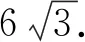
本题主要考查椭圆的定义、标准方程、直线与椭圆的位置关系、弦长公式、点到直线的距离公式、三角形的面积等多个知识点，对学生分析问题和解决问题的能力要求较高，特别强调利用韦达定理来解题时，一定要注意该定理所满足的条件，另外应用基本不等式求最值时要满足三个条件“一正二定三相等”，缺一不可.

2 甘肃省临泽县第一中学

祁居攀(邮编：734200)

导数及其应用的证明题一直以来都是以压轴题出现在高考试题中，是高考中的热点，也是学生学习的难点，学生在解答过程中一是找不到方法而无从下手，二是方法选择不合适导致半途而废，本文将学生做题中出现的错误加以分析，供读者借鉴学习！

题目已知函数f(x)=e2x-ex-ax,且f(x)≥0.

(1)求a的值；

(2)若f(x1)=f(x2),x1≠x2，求证：ex1+ex2>2.

解析因为f(0)=0，且f(x)≥0恒成立，所以f(0)是f(x)的最小值，也是极小值，它的必要条件是f′(0)=0，得a=1

以下证充分性：

当a=1时，f(x)=e2x-ex-x，则f′(x)=2e2x-ex-1=(2ex+1)(ex-1),

在(-∞,0)内f′(x)<0,f(x)单调递减；在(0，+∞)内f′(x)>0,f(x)单调递增.

故f(0)是f(x)的最小值，也是极小值.

综上得，a=1.

第二问解答

错解1 由(1)知当f(x1)=f(x2),x1≠x2时x1x2<0，不妨设x1<0

由e2x1-ex1-x1=e2x2-ex2-x2,得(ex1-ex2)(ex1+ex2-1)=x1-x2，

由x1<0x1-x2，即ex1-x1>ex2-x2，

设g(x)=ex-x，只需证g(x1)>g(x2)恒成立，即证g(x)在R上单调递增，

由g′(x)=ex-1，得

在(-∞,0)内，g′(x)<0,g(x)单调递减；在(0，+∞)内，g ′(x)>0,g(x)单调递增.

与已知所证相矛盾.

解答错了！错在哪里？

错因分析由于两变量x1、x2分布在了所构造函数的两个不同的单调区间，从而导致利用函数的单调性无法证明，也就是说一个不等式的证明，若构造的函数不合适将不一定能得到正确的证明.

正确解析由(1)知当f(x1)=f(x2),x1≠x2时，x1x2<0，不妨设x1<0

由e2x1-ex1-x1=e2x2-ex2-x2,得(ex1-ex2)(ex1+ex2-1)=x1-x2，

设g(t)=(t-2)et+t+2，则g′(t)=(t-1)et+1，

记h(t)=(t-1)et+1，则h′(t)=tet<0，

所以g′(t)在(-∞，0)内单调递减，故g′(t)>g′(0)=0，

所以g(t)在(-∞，0)内单调递增，故g(t)

即(t-2)et+t+2<0，所以原命题ex1+ex2>2成立.

错解2 设t=ex>0，所以f(t)=t2-t-lnt，

由f(x1)=f(x2),x1≠x2，则f(t1)=f(t2),t1≠t2，

由x1<0

要证ex1+ex2>2，即证t1+t2>2，即证t1>2-t2，

因为t1<1

由f(t1)-f(2-t2)=f(t2)-f(2-t2)，(t2>1)

令g(t)=f(t)-f(2-t),(t>1)

则g′(t)=f′(t)+f′(2-t),(t>1)

当1

当t>2时，g′(t)>0，g(t)单调递增.

所以g(t)≥g(2)

解到这里已经无法利用函数的单调性确定f(t)与f(2-t)的大小.

解答错了！错在哪里？

错因分析利用函数的单调性比较两变量的大小，则两变量必须在同一区间内，否则将无法比较，本题由于0

注意若把要证t1+t2>2，即证t1>2-t2改为证t2>2-t1情况会怎样呢？

正解解析接上面证明要证t1+t2>2，即证t2>2-t1，

因为t1<11,2-t1>1.

由f(t2)-f(2-t1)=f(t1)-f(2-t1)，(0

令g(t)=f(t)-f(2-t),(0

则g′(t)=f′(t)+f′(2-t),(0

故g(t)=f(t)-f(2-t),(0g(1)=0成立，即f(t)-f(2-t)>0.

所以f(t2)-f(2-t1)=f(t1)-f(2-t1)>0，

即f(t2)>f(2-t1)(下面证f(t)的单调性)

所以在(0，1)内f′(t)<0，f(t)单调递减，在(1，+∞)内f′(t)>0，f(t)单调递增.

所以在t2>1,2-t1>1时，由f(t2)>f(2-t1)，得t2>2-t1.

即证得t1+t2>2，原命题ex1+ex2>2成立.

总结提升(1)利用推理法证明不等式时每一步推理都要等价，否则会出现必要性成立而充分性不成立的情况.

(2)证明过程中所涉及的构造函数要符合本题自变量所限制的条件，否则会出现一些错误的结论.