讲题讲什么——由怎么做到怎么想

(邮编：225721)

江苏省兴化市戴泽初级中学

1 缘起

图1

题1 已知：如图1，△ABC中，D、E是BC上的点，满足BD=CE，AD=AE，∠1=∠2,试找出图中全等三角形，并说明理由.

师：请大家根据条件找出图中全等三角形，并说明理由.

生1：△ABD≌△ACE.由∠1=∠2，根据等角的补角相等，可得∠ADB=∠AEC,又BD=CE，AD=AE，可得△ABD≌△ACE(SAS).

生2：△ADC≌△AEB，由BD=CE，可得BD+DE=CE+DE，即BE=CD，又∠1=∠2，AD=AE，可得△ADC≌△AEB(SAS).

师：很好，大家都听懂了吗？好，看下一题.

这是笔者听到的师生解决问题时的一段对话，学生回答很正确，说理过程严谨，教师也给予积极评价，似乎很完美了.但学生在讲题过程中都在讲这道题怎么做，即问题的解决过程，没有怎么想的，即问题的分析过程.教师只评价对错，象征性地了解其他学生是否听懂，这就是目前普遍存在的只讲“怎么做”不讲“怎么想”的典型案例，那么这两者有何区别呢？会讲“怎么做”应该表明学生会做这道题了，但是缺少解题思路的分析，比如依据什么线索进行思考：怎么想到由∠1=∠2得，∠ADB=∠AEC，由BD=CE，得BE=CD，有没有其他全等三角形等等.而从听众角度分析，学生只听到“怎么做”，他们能理解其中的道理吗？今后可以解决类似问题吗？他们的收获有哪些？一切都不得而知!

讲“怎么做”是告诉听众要先这么做、再那么做，这与读参考答案有何区别！无论是讲题人还是听讲人都缺乏问题的分析过程和思维的发展过程，以致教学效果大打折扣.因此，在学生讲题，也包括教师讲题时，要从讲“怎么做”到讲“怎么想”，从关注解题过程到关注思维过程，揭示思维发生和发展的过程，促进对问题的深度思考.

2 有效追问，激发“怎么想”的意识

追问即追着问，在原有问题之后根据学生的回答进一步针对性提问，促进深层次思考[1].当学生只讲解题过程时，教师可以根据学生所讲内容进行追问，如“你是怎么想的”“哪些条件启发你这样做”“怎样启发别人也这样做”等，激发学生有条理思考问题的意识，引导学生关注方法的生成过程，会解释方法的合理性.

比如在学生回答题1后，教师应追问“你是怎么想到这两个三角形全等的”“怎么想到证∠ADB=∠AEC和BE=CD”，引导学生从图形直观和条件分析的角度进行思考.比如“由BD=CE，AD=AE分别在△ABD和△ACE中，猜想△ABD和△ACE全等，但是还缺一个条件，已知∠1=∠2，根据等角的补角相等，可得∠ADB=∠AEC，所以两三角形全等可证”，“由∠1=∠2，AD=AE分别在△ADC和△AEB中，但是还缺一个条件，已有BD=CE，可得BE=CD，所以全等可证”.像这样，通过追问，引导学生细化找全等、证全等的过程，可加深全等SAS方法的综合运用.

3 强化分析，指导“怎么想”的方法

数学家乔治·波利亚认为解题分析有四步骤：①弄清题意；②拟定计划；③实行计划；④回顾.只讲“怎么做”无疑是跳过第①、②步，直接到第③步.其实弄清题意是解题的重要基础，也就是明确条件是什么，由条件能得到什么结论，条件之间是否产生什么新结论，问题是什么，需要什么条件，与已有条件之间有什么联系等.教师应指导学生学习分析问题的方法，建构思考问题的策略.

3.1 想已知条件，由因执果，培养递进思维

条件是解决问题的线索，要重视条件的分析过程，引导学生理清有哪些条件，可得到哪些结论，逐渐逼近问题核心，使思维合理有据，解法自然生成.

图2

A. 6 B. 5 C. 4.8 D. 4

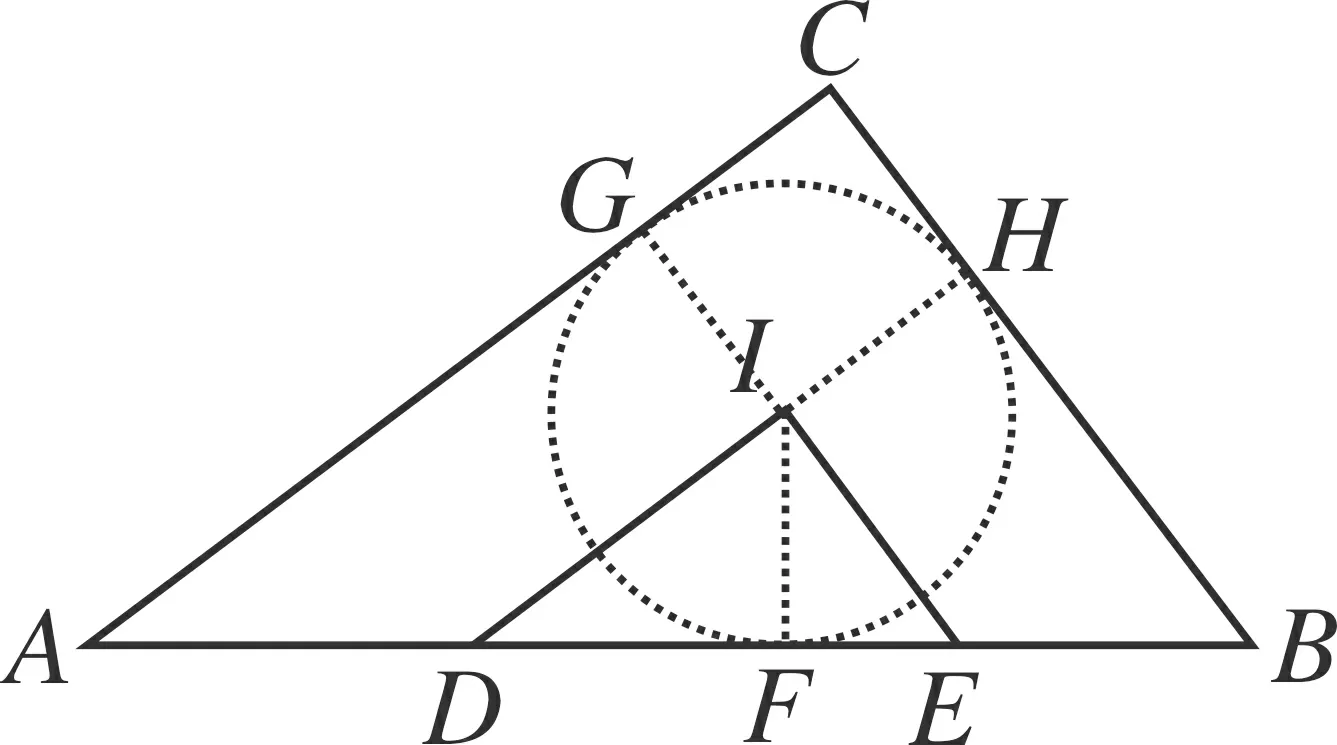
图3

思路1 如图3，由平行得△DEI∽△ABC，可用相似性质中周长比等于相似比，求出DI即可.由内心想内切圆，求出半径为1，在△DBH中求出DH就可以求出DI.

图4

思路2 如图4，与思路1类似，换一个角度求出DI.

思路3 如图5，与思路1类似，由相似性质中周长比等于对应边上高的比，求出CM即可.

图5

思路4 如图6，由内心想角平分线，加上直线平行，联想基本图形——平行+平分，可得两个等腰三角形，则△DEI的周长就是AB的长.

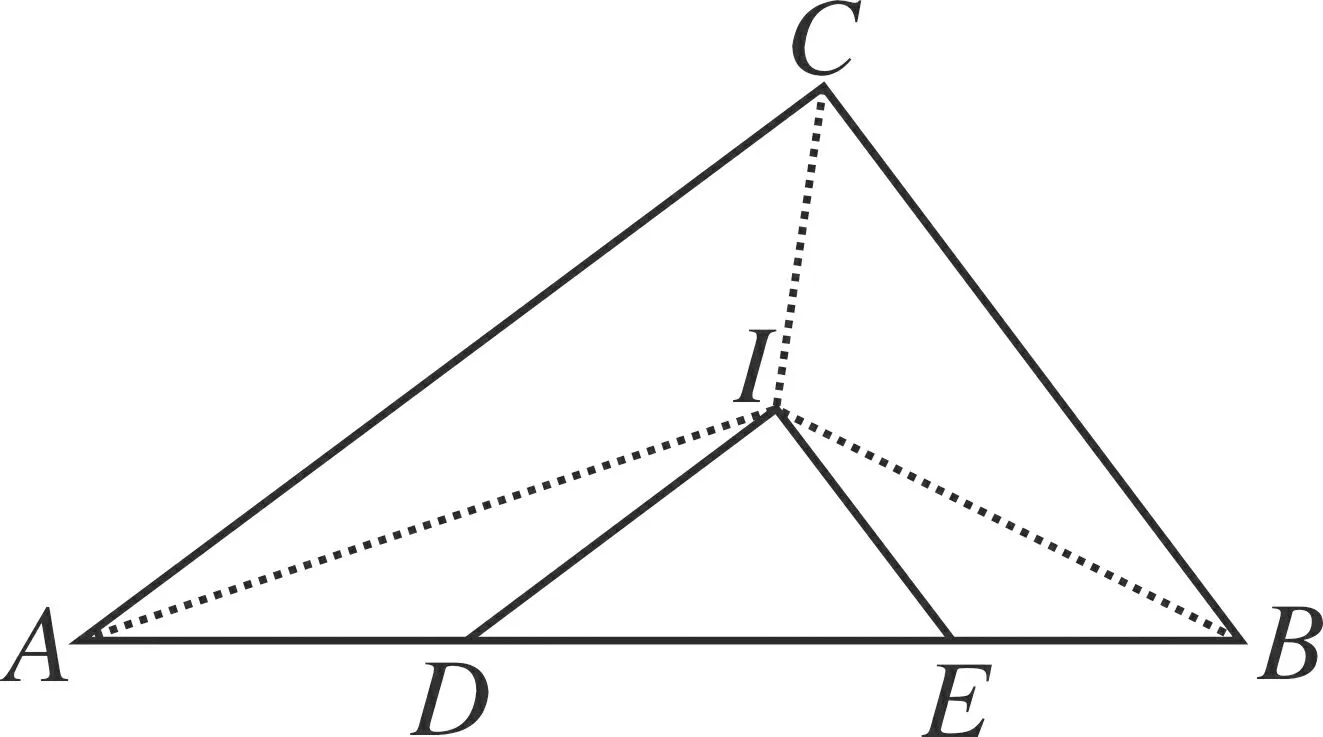
图6

像这样，只有让学生讲出分析条件的过程，才能加深对条件的多种理解，促进在联想中发现不同思路，在对比中辨别方法优劣.听众自然也经历了思考问题的全过程，感受由条件出发进行联想，尝试有条理地分析与表达，顺应思维的发展方向.

3.2 想问题解决，由果索因，培养逆向思维

从问题出发就是运用逆向思维，颇有点“反其道而思之”的意思， “李白打酒”是一个典型问题：李白街上走，提壶去打酒；遇店加一倍，见花喝一斗，三遇店和花，喝光壶中酒.试问酒壶中，原有多少酒？从正向思考，无疑需要列出较复杂的方程，但是从“喝光酒”思考，即壶中酒量为0往回推，问题随之轻松解决.

3.3 想因果联系，综合分析，培养整体思维

分析题目应引导学生准确找出条件和问题，充分挖掘条件的作用，分析条件能带来的结论，同时要分析解决问题需要什么条件，强化条件和结论之间的联系，整合双向资源，从而解决问题.

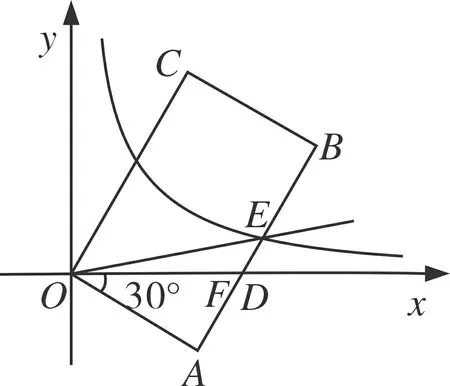
图7

图8

生：老师可以帮我讲一下这道题吗？题目条件多，没有思路.

师：我们一起来分析，从条件展开联想.

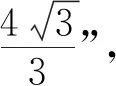
师：问题是“求k的值”，需要什么条件？

生：啊，这么简单啊，我会了，就是要分析条件中每一句话，找出条件与问题之间的联系啊！

像这样，并没有特殊的解题方法，只是充分挖掘条件和问题的内在联系，让思维层层递进，犹如剥洋葱般逐渐呈现真相，发现解决问题的方法.

4 重视积累，夯实“怎么想”的基础

建构主义学习理论认为：学习是引导学生从原有经验出发，生长(建构)起新的经验[2].已有经验是“怎么想”的基础，它是数学活动重要的知识储备、方法来源、思想载体，只有具备一定的数学活动经验，才能实现问题与已有经验的联系、整合、重组和优化.

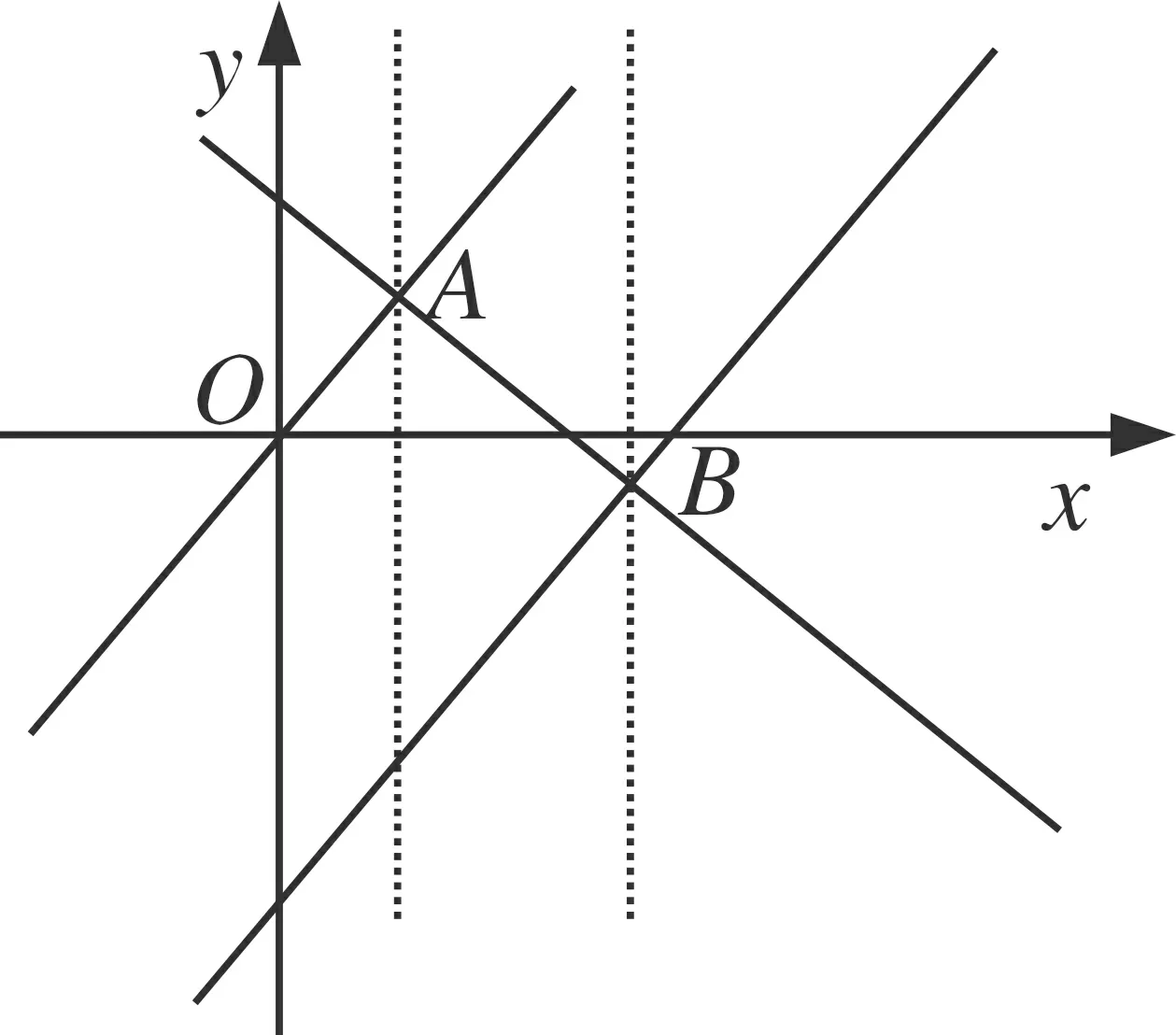
图9

师：刚才大家分析得都很好，求点B的横坐标是一个难点，请大家先独立思考5分钟，然后组内交流.

师：两位同学都发表自己的做法，就是用方程组求交点坐标.

图10

师：说得真好，生3创造性地从图形相似角度思考，方法简单易懂，尤其是思路清晰，讲出自己思考的过程，为你点赞！

本题中，学生将当前问题和已有经验进行联想，如不等式与函数关系，交点坐标的代数解法、函数平移变化性质、相似三角形判定与性质等，教师要引导学生积累解题活动经验，如代数中常见的式结构：乘法公式、方程模型、函数模型等，也可以是图形中的形结构：三角形基本变换、特殊四边形、圆中基本图形、函数与图形结合等.

5 重视交流展示，增强“怎么想”的动力

学生讲题的本质是师生交往互动的过程，应是主动活泼、富有个性的过程.教师应搭建学生交流展示的平台，对学生在讲题过程中的表现给与积极评价，让学生乐学、善讲、勤思，享受讲题成功的乐趣，增强思维发展的动力.

图11

题5 (2018 泰州)如图11，平面直角坐标系xOy中，点A的坐标为(9，6)，AB⊥y轴，垂足为B，点P从原点O出发向x轴正方向运动，同时，点Q从点A出发向点B运动，当点Q到达点B时，点P、Q同时停止运动，若点P与点Q的速度之比为1∶2，则下列说法正确的是( )

A．线段PQ始终经过点(2，3)

B．线段PQ始终经过点(3，2)

C．线段PQ始终经过点(2，2)

D．线段PQ不可能始终经过某一定点

师：请大家积极思考，有想法请说出来.

生1：点P、Q都在运动，是否可以表示出直线表达式？

生3：我来试试，去分母得(y-2)t=3y-2x，变形为(t-3)y=-2x+2t,要想过定点就是与t值无关，则t的系数为0，当y=2时，x=3,过定点(3,2).

师：讲得很好，用直线表达式求定点，但是运算量大了点，是不是有更简便的方法，谁能帮帮我？

图12

生4：我还有一个更好的方法.

师：真的吗？请你到讲台前告诉大家的想法.

其实，预设的方法就是求直线表达式，但是运算量大，不够简便，通过老师的“示弱”，有效激发学生思考的热情，促进学生借助图形深入思考，敏锐发现OP=2AQ比值不变联想到相似，从图形角度创新解决问题.

6 结语

“怎么做”与“怎么想”之间并无矛盾，并不是讲“怎么做”就不好，写此文的初心是为强化讲题时对思路的分析，强化对问题的深度思考，促进讲题人和听讲人思维的碰撞，引导学生建构解决问题的策略方法，消除机械模仿、缺乏理性思考的弊端.如果上升到培养人的角度，我们既需要行动的执行者，更需要行动的策划者、组织者，思想是行动的先导，思想是行动的指南，独立思考、精准表达应是现代人的良好品质！