对一道中考压轴题的再探究

(邮编：230061) (邮编：230061)

安徽省合肥市庐阳区教研室 安徽省合肥市第四十五中学

每年的中考几何压轴题都是老师和学生们关注的焦点，中考几何压轴题综合性强，考查的知识点多，图形纷繁复杂、千变万化，对学生们的思维能力和数学思想方法要求都比较高.学生在解题过程中往往因为辨析不出问题的本质，找不到解决问题的突破口而造成丢分.在中考几何压轴题的复习课教学中，老师要帮助学生学会分析问题的本质，抓住几何图形的变化规律，从本源出发，顺藤摸瓜，通过变式探究，解决疑难问题.

下面以一道中考题为例，从一个简单基本图形入手，层层递进，为读者们剖析简单图形到复杂图形的演变过程，希望对我们平时的几何复习课教学有所启发.

1 原题呈现

2016年安徽省中考数学第23题如下：

图1

如图1，A、B分别在射线OM、ON上，且∠MON为钝角.现以线段OA、OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP，△OBQ，点C、D、E分别是OA、OB、AB的中点.

(1)求证：△PCE≌△EDQ；

(2)延长PC，QD交于点R：

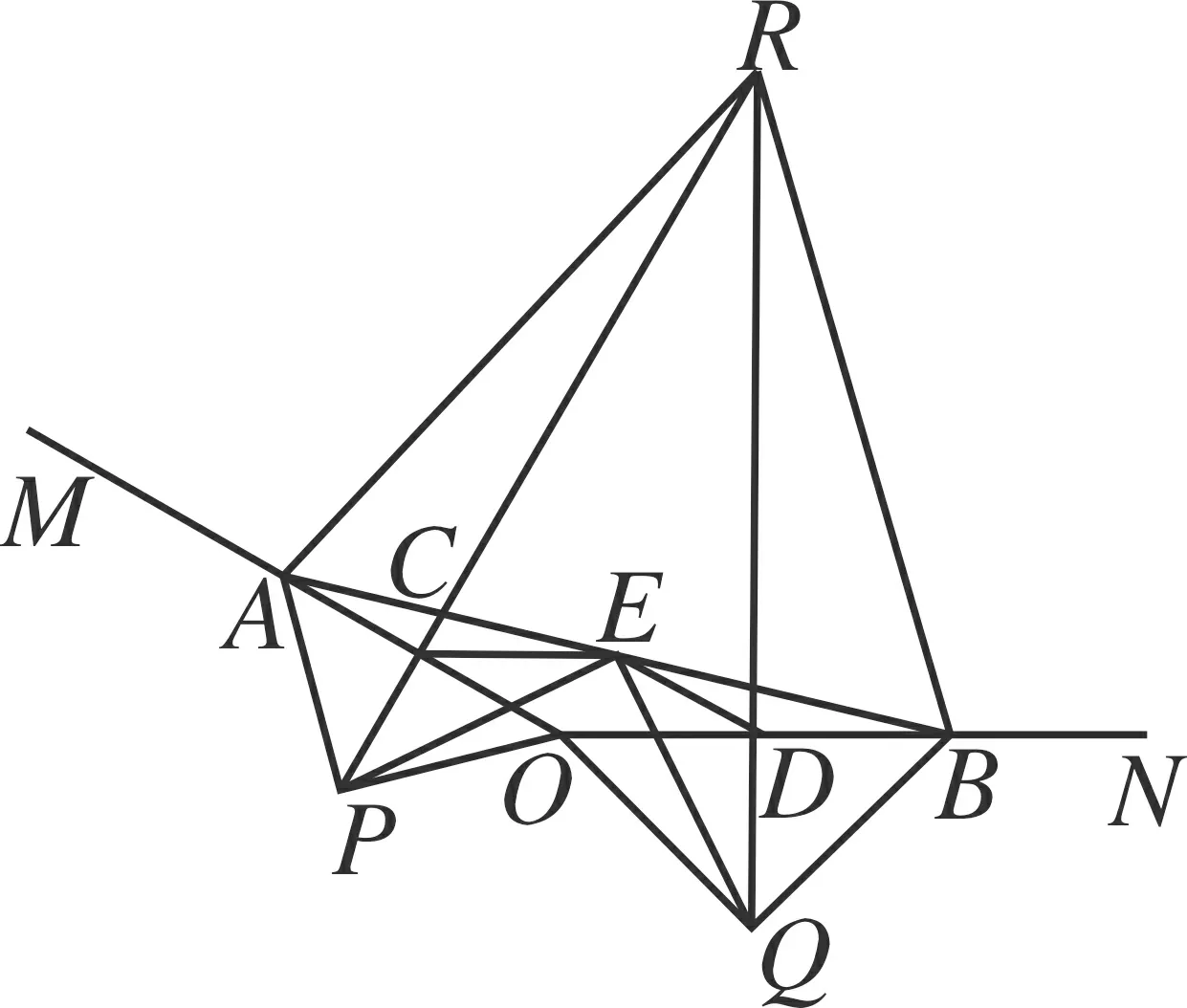
图2

①如图2，若∠MON=150°，求证：△ABR为等边三角形；

图3

②如图3，若△ARB∽△PEQ，求∠MON的大小和AB∶PQ的值.

本题综合考查了相似、中位线、直角三角形的性质，考查图形之间的变化及内在联系，综合性强，特别是图形线条较多，关系复杂，学生们看不懂图，读不懂题.眼花缭乱的图形让学生们找不到解决问题的突破口，这也是失分的关键原因.

但真的没有章法可循吗？要想认识本题，我们先从一个基本图形说起.

图4

2 追根溯源

问题1 如图4，△ABC中，AC=BC，过点A作AQ⊥BC于点Q，过点B作BP⊥AC于点P，E是AB的中点，连接PE、QE.求证：PE=QE.

证明因为BP⊥AC，所以∠APB=90°.在Rt△ABP中，

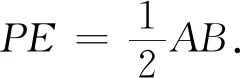
事实上，由于等腰三角形是轴对称图形，PE=QE是显然的，不仅如此，根据对称性，还能得到∠1=∠2.

上述关于线段长度和角度的关系是基于一类特殊的三角形——等腰三角形，于是可以作出大胆的猜想，在一般三角形中，此结论是否也成立呢？

图5

问题2如图5，△ABC中，过点A作AQ⊥BC于点Q，过点B作BP⊥AC于点P，E是AB的中点，连接PE、QE.求证：PE=QE，∠1=∠2.

证明与问题1证法同，得PE=QE.

在△AOP和△BOQ中，因为∠APO=∠BQO=90°,∠AOP=∠BOQ，所以∠1=∠2.

无论是在等腰三角形，还是一般三角形中，∠1=∠2这个结论都是成立的.现在换一个角度来分析这个问题，也就是说，若先假设∠1=∠2，那么PE=QE是否依然成立呢？

3 引申探究

依然从特殊的三角形——等腰三角形着手.

图6

问题3 如图6，△ABC中，AC=BC，O是△ABC内一点，且满足∠1=∠2，过O点分别作AC、BC的垂线，垂足分别为点P、Q，E是AB的中点，连接PE、QE.求证：PE=QE.

由等腰三角形的轴对称性，易得PE=QE.也可以借助全等三角形的相关知识加以证明.

探究之一

思考在一般的三角形中，结论PE=QE是否依然成立？

图7

问题4 如图7，△ABC中，O是△ABC内一点，且满足∠1=∠2，过O点分别作AC、BC的垂线，垂足分别为点P、Q，E是AB的中点，连接PE、QE.求证：PE=QE.

证明分别取OA、OB的中点F、D，连接PF、EF、QD、ED.

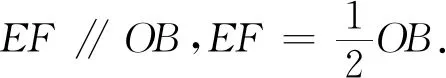
所以四边形ODEF是平行四边形，从而∠OFE=∠ODE.

因为∠PFO=2∠1，∠ODQ=2∠2，∠1=∠2，所以∠PFO=∠ODQ，从而∠PFE=∠EDQ.

所以PF=ED,EF=QD，从而△PFE≌△EDQ，故PE=QE.

探究之二

思考图中的∠PEQ与∠1、∠2有什么样的数量关系.

实验发现：

图8

特殊情况1 当∠1=∠2=30°时，如图8所示，运用几何画板，测量出∠PEQ=60°、即△PEQ是等边三角形.

图9

特殊情况2 当∠1=∠2=45°时，如图9所示，运用几何画板，测量出∠PEQ=90°，即△PEQ是等腰直角三角形.

猜想∠PEQ=2∠1.

下面借助于图9，给出详细的证明过程.

证明因为∠PEQ=∠DEF-(∠PEF+∠QED)， ∠DEF=∠AFE，

所以∠PEQ=∠AFE-(∠PEF+∠QED)=∠AFE-(∠PEF+∠EPF)

=∠AFE-(180°-∠PFE)

=∠AFE-(180°-∠PFO-∠EFO)

=∠AFE+∠EFO-180°+∠PFO

=∠PFO=2∠1.

4 试题形成

图10

在探究的过程中，我们发现，四边形CPOQ对于结论的推导是没有任何帮助的，在保证∠PAO=45°的基础上，把线段CP、CQ隐藏，就得到了图10所示的图形.

图11

如果把图10绕点O进行旋转得到图11，也就是2016年安徽省中考题的第23题的图1.在此基础上增加一些条件，就可以得到这道中考题的后面两个问题.2016年的安徽省中考第23题压轴题也就产生了.

2016年安徽省中考第23题，第(1)问证明两个三角形全等，学生找两条等边并不困难，难点在于如何找一对等角，而文中借助图9的探究之二证明的∠PEQ=2∠1的解题思路和第(1)问找等角，以及第(3)问求∠MON的度数，过程与方法是完全一致的.也就是说，如果我们在平时的课堂教学中，能重视基本图形的教学，引导学生注重图形之间的变化，那么这道压轴题解决起来就会轻松很多.

5 几点思考

关于中考前压轴类习题的教学，有以下几点需要老师们关注.

(1)关注学生们的最近思维发展区

“最近发展区”这一概念是由前苏联教育家维果茨基提出的，它指的是现有水平和潜在发展水平之间的幅度，也叫做“教学的最佳期”.“最近发展区”的“最近”是基点，“发展”是目标．维果茨基认为至少可以确定学生有两个发展水平：第一个是现有发展水平，是由已经完成的发展程序的结果形成的心理机能的发展水平，表现为学生能独立地、自如地完成教师提出的智力任务；第二个是潜在发展水平，是那些尚处于形成状态，表现为学生还不能独立地完成任务，但在教师帮助下，在集体活动中，通过训练和自己的努力才能完成的智力任务.在课堂教学活动中，关注学生思维最近发展区，就是在学生最需要的时候给予指点、鼓励和帮助，从学生已有的知识储备出发，通过教师合理的引导、指导，尊重知识的形成过程，通过观察、猜想、验证、证明等思维过程获取知识与能力，进而形成思想与方法.这也是以人为本教育理念的核心内容.

(2)注重学生数学活动经验的获得

这里所说及的经验是指学生们把现实生活中的问题抽象转化成数学问题的过程中，所经历的观察、实验、归纳、类比、猜想、验证、推理证明等方法，进而形成的抽象概括的能力，也包括在解决某些数学问题中发现问题、提出问题、分析并解决问题的数学素养.在处理某些一般性的结论时，往往先把问题特殊化，在特殊状态下去寻找某些结论，获得一些经验，再在一般状态下去思考特殊状态下的结论是否仍然成立.本文分析的2016安徽省中考第23题的研究过程就是反复运用了特殊到一般的研究思路.

(3)学会研究动态问题中某些内在的规律

图形的变化纷繁复杂，点的运动、线的运动亦或是图形的运动，势必造成线段的长短变化、角度的大小变化、乃至图形的形状、位置等发生变化.在这些变化过程中有可能有某些亘古不变的内在规律，我们要带领学生们学会发现这些规律、研究这些规律、提出合理的观点与结论，进而推导证明这些结论与规律，这也既是数学教育的核心素养所在，也是几何教学的魅力所在.

波利亚曾说过：“解题的成功，要靠正确地转化.”教师在教学中要不断引导学生进行解题回顾与反思，帮助学生梳理、提炼基本图形，遇到问题时分离出基本图形，基本图形残缺时，构造基本图形，这样可以以这些基本图形为载体，培养学生的识图能力、分析推理能力. 实践证明：它是一种非常重要的，而且是行之有效的方法. 可以说：一张基本图形胜似千言万语！