无锡中考“尺规作图”题特色分析及教学启示
(邮编:214443)(邮编:214443)
江苏省江阴市第一初级中学 江苏省江阴市夏港实验学校
纵观全国各地的数学中考试题,因地域的不同而各具特色,如天津市的格点画图问题、北京市的阅读理解型压轴题、无锡市的尺规作图问题等都成为地区中考试题的名片和标签.历经传承和发展的这些试题凝聚了命题者的智慧,彰显了试题的特色和创新,而对这些试题特色的研究,有利于一线教师精准把握教学方向,最大限度地提高学生的思维能力.本文主要阐述无锡市数学中考尺规作图题的特色和教学启示,以期引起同行的深入探讨.
1 试题特色
1.1 作图与推理“嫁接”
数学是一门培养思维能力的学科,苏联教育家托利亚尔在《数学教育学》一书中指出:“数学教学是数学(思维)活动的教学.”可见培养思维能力在数学教学中的重要地位.其中,“推理能力”被规定为在数学课程中应该注重发展学生的“十个核心关键词”之一,作为数学学科初中阶段的培养目标.

图1
案例1 (2018·无锡)如图1,平面直角坐标系中,已知点B的坐标为(6,4).
(1) 请用直尺(不带刻度)和圆规作一条直线AC,它与x轴和y轴的正半轴分别交于点A和点C,且使∠ABC=90°,△ABC与△AOC的面积相等.(作图不必写作法,但要保留作图痕迹)
(2) 问:(1)中这样的直线AC是否惟一?若惟一,请说明理由;若不惟一,请在图中画出所有这样的直线AC,并写出与之对应的函数表达式.

图2

整个题目以推理立意,学生必须在分类的基础上,全面地考虑问题,把问题所有情形都要画出来,要求学生思维有较强的缜密性.解决此问题思维深刻性体现在要根据条件△ABC与△AOC的面积相等迅速得出直线AC始终经过OB中点的结论,抓住了这个本质问题进行深入细致的分析,实际上是直线AC绕OB的中点旋转,需要空间想象能力,善于运用集中思维,把思考方向集中到∠ABC=90°,运用交轨法分析才能解决问题.试题以画图为依托,在限制了面积相等和直角的条件下,通过分析才能找到作图的方向,其本质还是回归到几何图形的性质和几何图形之间的联系.
1.2 作图与数学活动“链接”
史宁中教授认为:作为创新能力思维基础的归纳能力,是建立在实践的基础上的,更多地依赖于过程,依赖于经验的积累.《义务教育数学课程标准》(2011年版)(以下简称《课标》(2011年版))指出,教师教学应使学生掌握基本数学知识和技能,体会和运用数学思想方法,获得基本的数学活动经验,并提出了“四基”的基本理念.数学实验、操作、推理等数学活动是积累数学活动经验的绝佳途径,而实际教学中很多教师忽视数学学习的过程价值,尺规作图考查数学活动和探究过程,试题较好地体现了课程标准的思想.

图3
案例2 (2014·无锡)(1)如图3,Rt△ABC中,∠B=90°,AB=2BC.现以C为圆心、CB为半径画弧交边AC于D,再以A为圆心,AD长为半径画弧交边AB于E.

(2)如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫作黄金三角形.请以以图4中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.(注:直尺没有刻度!作图不要求写作法,但要保留作图痕迹,并对作图中涉及的点用字母进行标注)

图4
分析
1.3 作图与数学实验“融合”
《课标》(2011年版)把创新意识放在突出重要的位置,而数学实验是培养学生创新意思的有效途径.在教学中,很多教师仅仅满足于数学知识的教学和数学思想方法的教学,对学生创新意识的培养并没有引起足够的重视,教学还没有提高到育人的高度,而研究能够考查学生创新能力的试题对教学中培养学生的创新意识和、提高数学教育的育人价值是很有益的.

图5
案例3 (2106·无锡)如图5,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC.
(1)线段BC的长等于___________;
(2)请在图中按下列要求逐一操作,并回答问题:

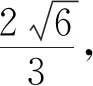
分析此题也可以看作是数学实验题,难点和亮点在第(2)②题,问题的实质就是把线段OD三等分,所以联结CD,过点A作CD的平行线即可,这是考试中考生普遍作法.也有考生是运用平行线分线段成比例定理或三角形重心性质来完成作图.当然最为简洁的作法是过点A作OD的垂线,垂足为P,则点P就是所求作的点.问题的解法入口较宽,但都要求学生善于对数学问题进行转化,即能运用所学的知识把一条线段三等份,对问题的特征和隐含的关系进行具体的分析.不同的作法,体现了学生扎实的几何基础,强大的几何构图能力,数形结合等数学思想高度自动化的运用能力.这样的考查方式不同于一般的证明题,已知条件来证明结论,思考方向明确,而需要学生根据已知条件自己探究到达结论的路径,需要思维灵活.多种解法能启迪学生多方向、多角度思考,体现思维的广阔性.学生的多种创新解法显示学生思维活跃、多谋善变,其思维具有发散性和直觉性.
2 教学启示
2.1 摈弃模型教学

2.2 凸显思维方法
数学是一门培养思维能力的学科,而尺规作图恰好能够考查学生思考问题的方法,展示思维的过程,强调思维的开放性、深刻性、灵活性、发散性.这些试题的出现对教师的教学提出了更高的要求,如果平时的教学就题论题,不注重思维方式的引导和培养,学生在考场中就很难适应此类试题,从无锡地区近几年的中考来看,学生在此类问题上的失分是比较严重的.从思维方式来看,一般的思维方式有:比较、分析、综合、抽象、概括等,而对于数学学科来说,归纳推理和演绎推理是最为重要的思维方式,类比和联想,一般化和特殊化的思维方法是教学中必须要教会学生使用.尺规作图问题,表面来看是作图,实际上考查的就是学生的思维方式和思维能力,很多问题都适合用分析法来解决问题,即假设图形已经做好,需要满足何种条件,再转化为基本作图来解决问题,当然对于思维能力较强的学生,用综合法也未尝不可,很多问题虽然作图的结果(结论)是一定的,但问题成立的条件却有很多,问题的开放程度高,需要有较强的逆向思维能力,如果教师平时教学没有真正重视思维能力的教学,考场失分是理所当然的事情.案例1中的第(2)题发现圆心必在OB的垂直平分线上,得出OA=BA,这是典型的运用分析法解题,即由果索因.如果学生缺少这些思维方法,思路就会受阻,思维就缺乏广阔性和灵活性,可见数学教学应把数学思维方式、方法的教学放在突出重要的位置.
2.3 重视核心素养
随着社会和经济的发展,学生的核心素养的培养将会成为学科教学的重点,从数学学科的特点来看,可以在教学中培养学生的6大素养即:数学抽象、数学直观、逻辑推理、数学运算、数学建模、数据分析.2011版的数学课程标准还提出了培养学生数感、符号意识、创新意识、应用意识.纵观无锡市中考数学试题的尺规作图问题,很好地契合了上述要求,如案例3第(2)题的②,从阅卷的结果来看,学生的作法就有二十多种,其中过点A作OD的垂线,就很好地体现了数形结合的思想、几何直观能力,以及强大的创新意识,思维深刻而又简洁.案例1的第(2)题,要证明直线AC的不惟一性,需要学生有较强的逻辑推理能力,试题的难度和考查点,都集中于此,就是以尺规作图为载体,考查学生的逻辑推理能力.这些试题引导教师在平时的教学中要立意高远,根据数学学科的特点,以培养思维能力为核心,落实数学核心素养,真正发挥数学学科的育人价值.

