由一道求比值问题所引发的探究与思考

(邮编：200435 )

上海市岭南中学

1 问题提出

图1

图2

2 三点探究

2.1 如何证明D、E、F三点共线？

2.2 图2的辅助线生成点到底在哪里？

既然证明D、E、F三点共线比较棘手，不如反其道而行之，直接延长DE至点F，使EF=BE，连接CF与AF，那么四边形ABCF为正方形吗？即△ABD与△FCD全等吗？遗憾的是依据该辅助线的作法不易证明．注意到两三角形确实全等且BD=CD、∠EDC=∠ADB，不妨延长DE后使DF=DA，则△FCD≌△ABD，得FC=AB且∠FCD=∠ABD=90°(即四边形ABCF为正方形)，易证△BCE≌△FCE得BE=FE，问题迎刃而解．当然，图2的辅助线也可描述为“过点C作CF⊥BC，交DE延长线于点F”，证明也是手到擒来之举．

综合分析上述两种方法可知，辅助线生成点本质在于如何把两条线段BE与ED整合成一条线段DF，从而把三条线段间的比转化为两条线段间的比．因此，由等腰直角三角形想到补为正方形看似精彩，但却只是一种表象，属于特殊条件下的技巧性处理，不具有一般性．

图3

既然是把线段BE与DE整合成一条线段，那么能否把它们直接整合在射线BE上呢？当然直接在BE的延长线上截取EP=ED不易处理，但过点C作BC的垂线BP并截取CP=CD，连接EP、BP(如图3)，则易证△ABD≌△BCP且△CDE≌△CPE，得∠BPC=∠ADB=∠EDC=∠EPC，即B、E、P三点共线，仿上也可求得比值．

图4

2.3 求线段比有哪些转化策略？

策略一求值计算转化

图5

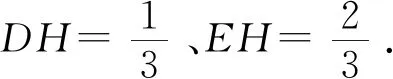
第二、求出所求比的两条线段与第三条线段间的数量关系．

图6

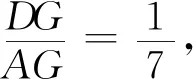
第三、直接计算两线段的长度

图7

策略二利用比例转化．

图8

例4 (2018年大连市中考第25题)如图8，△ABC中，点D在AB上，点E在BC上，且∠BDE=2∠ABC，点F在BD上，且∠AFE=∠BAC，延长DC、FE，相交于点G，且∠DGF=∠BDE．

(1)在图中找出与∠DEF相等的角，并加以证明；

(2)若AB=kDF，猜想线段DE与DB的数量关系，并证明你的猜想．

说明课前三天笔者就把例1与网友提供的图2印发给学生，同时抛出了上述三个思考问题，并要求学生对自己研究的结论或观点应提供配套习题加以佐证．上面是笔者依据课堂探究结果整理而得，其中例2与例4由笔者提供并当堂完成，而作为2019年本区一模考填空题压轴题的例3并非课堂上的探究题，原题由学生抄自教辅资料．不过令人欣慰的是，在本次一模测试中笔者所任教班级例3的得分率为0.57，远超于区0.28的平均水平，可见课堂教学效果发挥了关键作用．另外，课堂上还处理了学生课前准备的两道证明三点共线题，限于篇幅整理时略去．

3 三点思考

3.1 习题教学应避免“就题秀法”

“就题论题”现象虽然在日常教学中依然有一定的“市场”，但毕竟容易遭到诟病，因此在各类展示课与比赛课中已难得一见，取而代之的是“一题多解”“一模多能”或“一图一课(其实就是一题多变)”等更加开放性的习题教学新模式．单就“一题多解”的课堂教学而言，笔者经过长期观察发现：其基本流程往往只是不同解法的一一展示，缺少对方法生成的本质挖掘，似有“秀”方法之嫌．另外，发表在各类数学杂志上“一题多解”类文章有些也只是把各种解法进行简单罗列，对“为什么会产生一题多解”缺乏深层次挖掘，也有见“法”不见“理”之感，对习题教学可能会存在一定的误导．相反，笔者正是从挖掘辅助线的生成本源入手，揭示了例1中图2的辅助线并非源于“补形”，而是意在将分子中的两条线段整合成一条线段(即把三条线段之比转化为两条线段之比)，进而从“截长补短”角度生成出一题多解．然后又从“如何求线段比”入手，打开生成“一题多解”的另一扇窗．特别是思路分析也并非解题过程的简单呈现，而是从“知识转化”角度详细剖析思维生成的来龙去脉，不仅讲清“怎样做”，还着重明析“为什么这样做”，引导学生学会“怎样想”，为提升学生分析问题的转化能力奠定坚实的基础．

3.2 习题教学应注重“以题会类”

虽然“题海战术”之弊人皆知之，但“反复刷题”却又让不少同仁欲罢不能，其中缘由固然复杂，但缺乏“以题会类”的教学意识恐怕也是不容忽视的重要因素之一．课堂上，笔者以追求“以题会类”的习题教学最高境界为重，从知识转化角度，借助“知识溯源(回顾初中阶段与解题目标相关的知识源)”，针对“如何证明三点共线”归纳了四种常见的处理方法，又通过四道例题详细剖析了“如何求线段比”的转化策略，明析处理这两类问题的主要思考方向，并针对不同题目详细分析如何依据条件而选择适当知识源进行转化的策略解读与示范操作，极大地提升了学生处理同类问题的迁移与类化能力．

3.3 习题教学应突出“能力为重”

令人欣慰的是，“以发展学生思维能力为重”的习题教学观早已深深植根于广大同仁的育人理念，不过究竟如何发展学生的思维能力还是仁者见仁智者见智．对此，笔者的实践体会是务必要坚持三点：第一、完善学生处理问题的思维方式是发展思维能力的基础．与只教“做法”不同，笔者还长期坚持教“想法”，引导学生用“知识溯源式目标分析法”解决问题，从而学会“怎样想”．所谓“知识溯源式目标分析法”主要分为三步——首先要明确问题的目标是什么(如例1的目标就是求线段之比)、其次追溯初中阶段与目标相关的知识源(如求线段比的知识源主要有计算与比例转化两大类)、最后依据题目条件选择合适的知识源逐步转化(如例1依据特殊的等腰直角三角形和中点等条件宜选择通过计算求比值)；第二、丰富学生处理问题的转化策略是发展思维能力的关键．解题中思维受阻是无法避免的，这就要求学生要具备丰富的转化策略，积极调控受阻思维，突破难点．虽然转化策略在形式上千变万化(如化复杂为简单、化陌生为熟悉、化繁难为简易、化一般为特殊、化综合为单一、化高维为低维等)，但依据“所有数学问题都是运用所学过的知识解决的”可知“知识转化”才是一切转化之源(无论是“求线段之比”还是“证明三点共线”都体现了“知识转化”精髓；即使对于“截长补短”，在把线段不等关系转化为相等关系再转化三角形全等的转化线路图中，也凸显了“知识转化”的主线)．因此，实际教学中只有坚持以“知识转化”为本，才能真正丰富学生的转化策略，提升他们的转化能力；第三、发挥学生处理问题的能动性是发展思维能力的保障．毫无疑问，课前抛出问题以留给学生足够的思考与探究时间、课堂上放手让学生畅谈自己的想法与做法、课后鼓励学生进一步探究与质疑等系列举措，积极发挥了学生参与问题解决的能动性，激活了他们思维的主动性与创造性，全面地提升了他们的思维能力．

当然，如何加强对习题潜在功能的挖掘是一个永恒的开放性主题，也值得大家深度思考与进一步探索．