2019年高考浙江卷第21题的探究及教学启示

(邮编：323000)

浙江省丽水中学

2019年浙江高考结束后，关于数学试题偏难的消息铺天盖地.学生普遍认为解析几何题难入手，变元之间难转化，甚至有种解析几何“白学”的感觉.浙江高考卷向来重视学生的数学能力考查，我觉得2019年第21题是对学生解析几何基本能力的很好考查，是让学生理解解析几何是坐标几何的经典例题，有利于培养学生的数学建模和数学运算等核心素养.下面我们一起来欣赏这道题的风采.

1 题目呈现

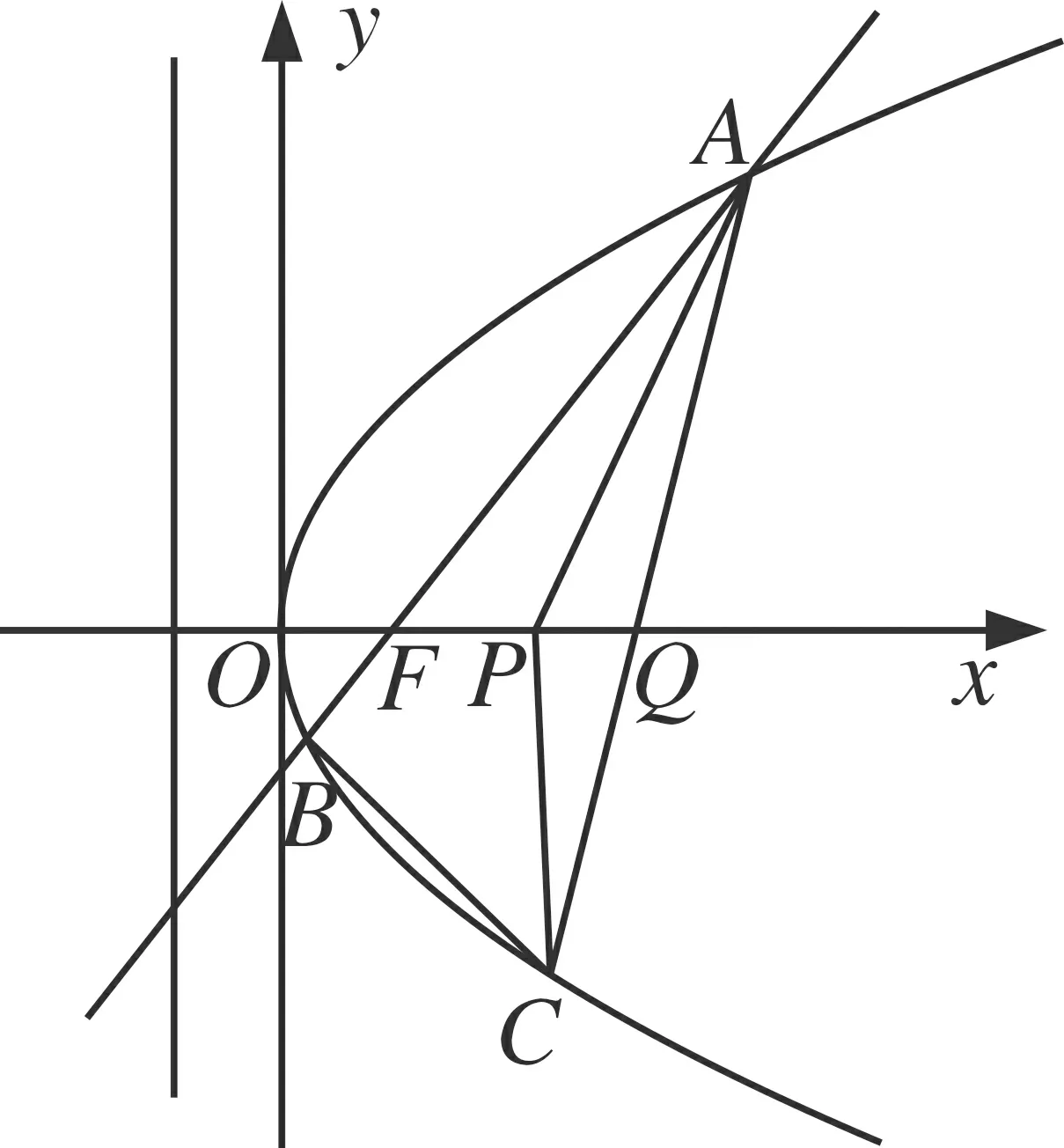
图1

(2019年高考浙江卷第21题)过焦点F(1, 0)的直线与抛物线y2=2px(p>0)交于A,B两点，点C在抛物线上，△ABC的重心P在x轴上，直线AC交x轴于点Q(点Q在点F右侧)．

(1)求抛物线的方程及准线方程；

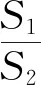
条件分析由焦点坐标可以求得抛物线方程是y2=4x，准线方程是x=-1.

第二问是求两块面积之比，由于A,B,C三个点都是动点，所以学生在考场里面就觉得题目难入手，找不到问题的突破口.波利亚在著作《怎样解题》中提出了一个有名的解题理论表：

下面我们将根据波利亚的解题理论表展开解题策略探究.

策略一设点参数建立单参数函数模型

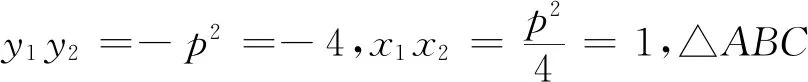
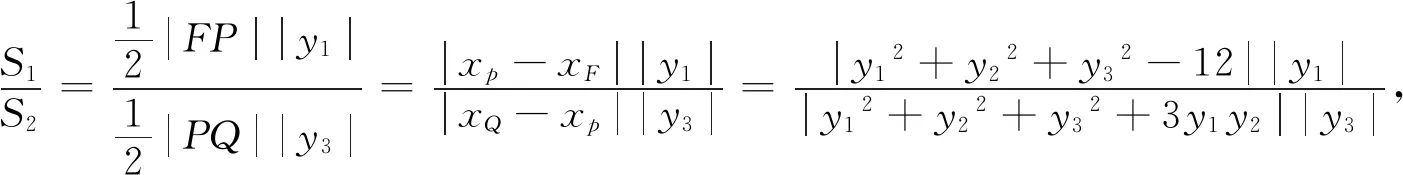
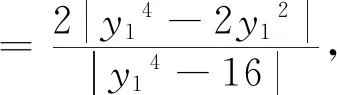
点评策略一是由焦点弦性质得到A，B两点的坐标关系，由重心坐标关系进而得到A，B，C三点的纵坐标之间的关系. 通过直线的点参数方程，代数化的面积比表达式中每一个量都可以用y1表示，最终建立关于y1的目标函数，需要学生具备很好的转化与化归能力.在消元的过程中需要有很好的数学运算能力，我们在平时的教学过程中更多的要让学生动手计算，体验解析几何中坐标间的相互转化，这与解析几何培养学生数学运算能力的初衷是一致的.点参数的思想方法与解析几何是坐标几何的本质相吻合.但是这种策略计算量大，考试的有限时间内需要我们进一步挖掘题目的几何背景.

策略二挖掘几何背景构建单参数函数模型

解析由于点P是△ABC的重心，连接BP，则SAPB=SAPC，

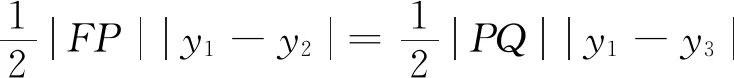
图2

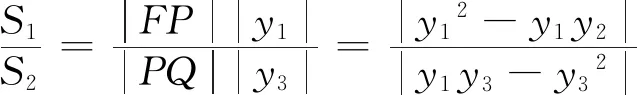
目标函数处理策略一

目标函数处理策略二

目标函数是关于y1的高次分式函数，通过抛物线方程降次，因为y12=4x1

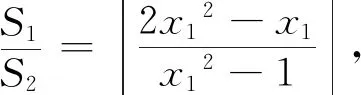
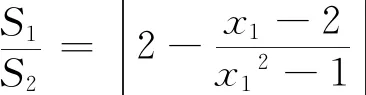
点评策略二是在挖掘题目几何背景后巧妙地得到面积比的函数模型，解析几何是用代数的方法解决几何关系与性质的一门几何学分支，利用重心这一几何性质得到面积相等，可以用纵坐标表示底边之比，进而建立面积比的函数模型，几何代数相得益彰，与解析几何的思想方法相辅相成.解析几何的教学要引导学生善于发现几何背景，善于化归几何关系，善于几何关系代数化.

策略三借助几何性质构建双参数函数模型

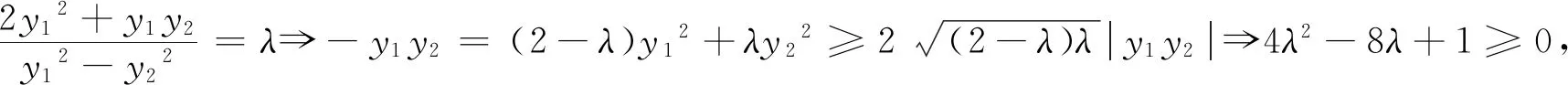
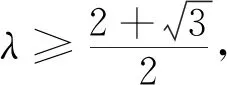
故P(2,0).

点评多元最值问题常用的方法是消元，同时也要分析题目条件与目标的结构，积定平方和最小这样的不等式思想引导我们建立二元目标函数，这也体现了不等式是处理解析几何目标函数的重要方法，与解析几何韦达定理设而不求的思想相辅相成！

策略四设直线构建单参数函数模型

解析设直线lAB:x=ty+1,则

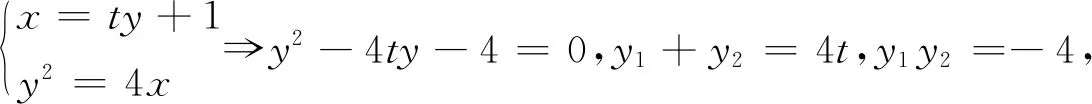
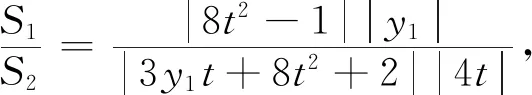
点评设斜率参数求解表达式最后的结果是关于y1和t双元函数，通过韦达定理容易消去t，得到与策略一一样目标函数，问题最后还是回归到点参数上，与命题者的初衷一致.

策略五借助平面向量基本定理构建单参数函数模型

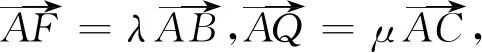
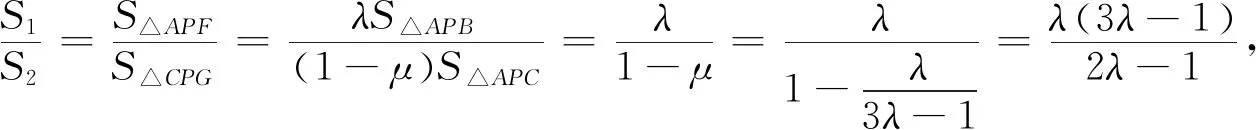
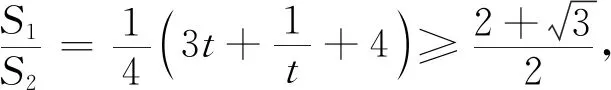
点评平面向量在几何问题中有独特的优势，用向量基本定理构建面积比函数模型，感悟“基”的思想，正是数学知识融会贯通的体现.通过分析发现策略四解题过程中并没有用到抛物线的方程以及性质.由图形可知这道题明显考察直线与抛物线综合问题，为什么可以离开抛物线解题？P点坐标又怎么求？带着疑问进一步挖掘题目的命制背景.

深度挖掘题目命制背景

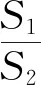
点评命题背景其实是三角形中有关重心面积比最值的问题，这个问题与抛物线没有任何关系，只是通过将三角形置于抛物线中，探究△ABC三点坐标间的关系求解重心坐标，考查了直线与抛物线相交弦性质，这也是命题者一定要求解重心坐标的原因.

3 变式提升

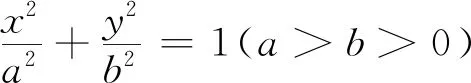
条件分析将抛物线改为椭圆，A、B仍然满足焦点弦性质，点C在抛物线上，没有改变问题的本质,弄清了题目的本质，其实点C在什么位置是没有关系的.

图3

变式2 (2019湖州三校联考)已知抛物线L:y2=2px(p>0)的焦点为F，过点M(5,0)的动直线l与抛物线L交于A,B两点，直线AF交抛物线L于另一点C，|AC|的最小值为4.

(1)求抛物线方程；

(2)记△ABC,△AMF的面积分别为S1,S2，求S1·S2的最小值.

条件分析A(x1,y1),B(x2,y2),C(x3,y3)，y1·y2=-20，

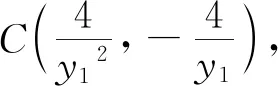
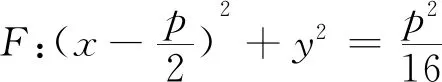
(1)求抛物线C的方程；

(2)设点M(t,0)，N(2t,0)(t为正常数)，直线PM，PN分别交抛物线C于A、B两点，求△ABP面积取最小值时点P的坐标.

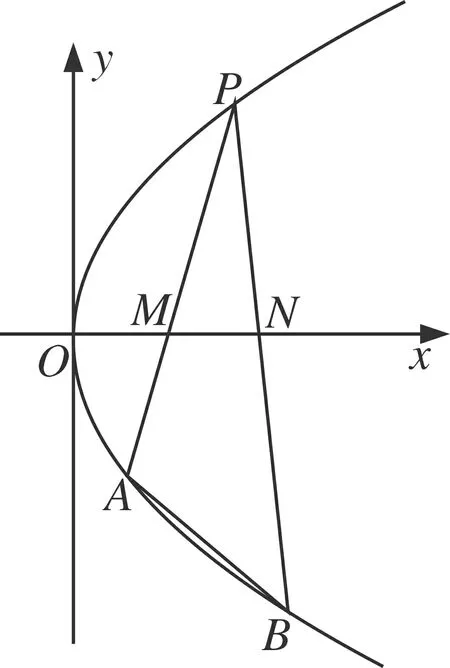
图4

条件分析C:y2=4x，P(x0,y0),A(x1,y1),B(x2,y2)，可求得

实现了三个点坐标间的相互转化.下面解法同理2019年浙江卷21题.

点评变式2与变式3坐标间相互转化的思想与高考题的思想是一致的，只是高考题几何味道浓一点，需要学生利用重心化归面积比函数模型，更加体现解析几何的本质.

4 题目价值

设点与设线是处理直线与圆锥曲线综合问题最基本的方法，本道抛物线与直线的综合问题需要学生发现问题的几何背景并且厘清题目中三个动点之间的关系，用点参数建立模型比斜率参数建立模型容易处理，这与学生的一贯思维有所区别，启示学生不能思维定式，要具备分析问题，解决问题的能力.很好地体现了解析几何是坐标几何这一重要特征.题目注重考查学生的数学建模，数学运算等核心素养.重视解析几何本质问题的探究，体现了想的多一点的命题理念.有利于引导高中数学突出数学本质，重视学生对数学的探究；有利于落实新课程改革精神，实现高中数学教学的高质量运行，进一步推动中学的素质教育.

5 教学反思