“龙江2号”月球轨道微卫星定轨分析

欧阳琦，牛东文

（北京航天飞行控制中心，北京100094）

引 言

随着现代科学技术的发展，技术性能强，功能密度高的微纳卫星成为各国研究的热点。微纳卫星建立在微电子学、微型机械、微加工等现代航天高科技基础上，具有成本低、重量轻、体积小、性能高、研制周期短等特点，在实现全球通信、对地观测以及快速反应的军事侦查等方面起到了重要作用[1]。微纳卫星已经在近地空间得到了广泛应用，近年来，美国国家航空航天局（National Aeronautics and Space Adminis‐tration，NASA）和欧洲航天局（European Space Agency，ESA）等国际航天机构也纷纷将微纳卫星引入到深空探测项目中，以实现探测任务效益的最大化。INSPIRE（Interplanetary Nanospacecraft In a Rel‐evant Environment）是喷气推进实验室（Jet Propul‐sion Laboratory，JPL）规划的利用微纳卫星探测深空的首个任务，任务计划将两颗3U微纳卫星送入太空，并飞离地球150 万km，以验证微纳卫星在深空中的生存能力。NASA也将于2020年在发射Orion EM1时搭载发射13颗微纳卫星用于深空探测[2]。

我国近年来也开展了微纳卫星深空探测的相关任务。为充分利用“嫦娥4号”中继星任务发射过程中的运载剩余能力，哈尔滨工业大学研制的月球轨道天文观测微卫星“龙江2 号”已于2018 年5 月21 日随“嫦娥4号”中继星搭载发射。“龙江2号”质量只有47 kg，2018 年5 月25 日进入环月轨道，并成功完成了对月成像任务，成为全球首个独立完成地月转移、近月制动、环月飞行的微卫星[3]。

在微纳卫星深空探测任务中，为充分利用一次深空探测任务的运载能力，通常通过搭载等形式将多颗微纳卫星与主探测器同时送入探测轨道。由于深空测控资源有限，在任务的实施过程中，测控资源通常优先保障主探测器任务，分配给微纳卫星的测轨时间较少。由于轨道计算精度对于探月任务的成功实施至关重要，有必要对有限测控资源条件下微纳卫星的定轨精度进行分析。本文以微纳卫星深空探测为背景，采用“龙江2号”微卫星的轨道测量数据对其定轨精度进行分析。介绍了微卫星飞行任务及其飞行过程中影响测定轨的因素，并对微卫星地月转移段和环月段的定轨精度进行了分析，为后续微纳卫星深空探测的轨道确定提供有益参考。

1 任务分析

1.1 “龙江2号”微卫星飞行任务

“龙江2 号”微卫星与运载火箭分离后，单独完成地月转移、近月制动阶段的飞行，最终进入环月轨道。微卫星系统的飞行过程如图1 所示[4]。微卫星在地月转移段的主要动作包括微卫星对日定向，多次轨道中途修正，直至达到月球近月点附近。进入环月轨道后，微卫星择机进入对月成像模式。

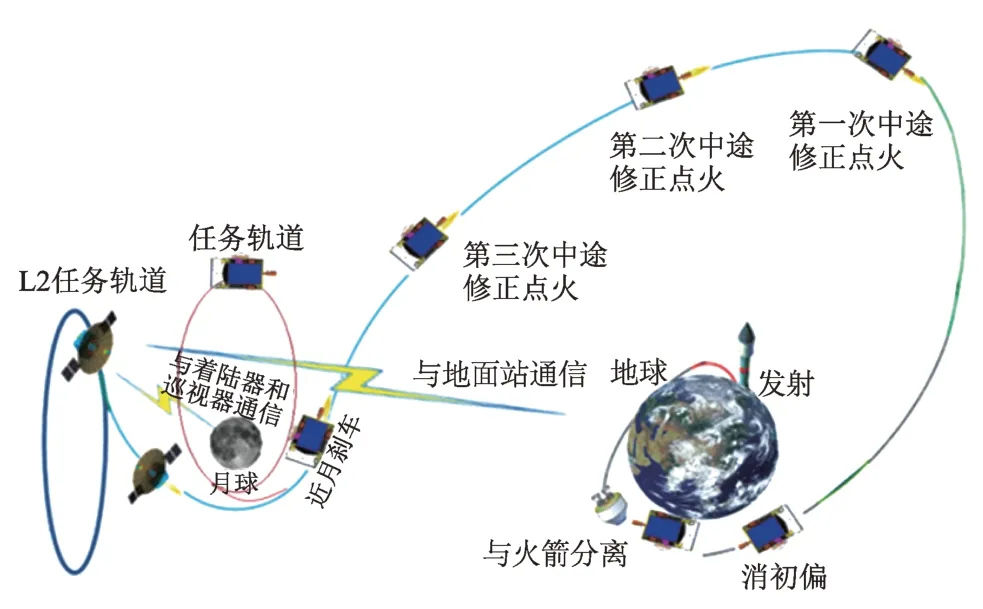
图1 “龙江2号”飞行过程Fig.1 Mission flight process of Longjiang-2

1.2 观测数据

“龙江2 号”于2018 年5 月21 日发射升空，经过2 次中途修正、近月制动后，于2018 年5 月25 日22时进入近月点高度约为350 km，远月点高度约为13 700 km的环月大椭圆轨道，周期约为20.4 h。本文对该卫星地月转移段以及环月段的轨道精度进行分析，其 中环月段采 用 2018 年 5 月 30 日—2018 年 7 月19日期间的测量数据。在地月转移段，圣地亚哥站、佳木斯站、纳米比亚站、喀什站以及青岛站参与了微卫星的测轨；在环月段，青岛站、喀什站和纳米比亚站对微卫星进行了测轨，测量数据包括USB 测距和测速，测站分布如图2所示。环月段测控资源相对紧张，每天有两站跟踪，共约3～4 h的轨道测量数据。

图2 测站分布图Fig.2 Station location

1.3 动量轮卸载

微卫星姿态控制系统采用了整星零动量的三轴稳定方案，星上装有动量轮和推力器。动量轮以内力矩作为控制力矩，通过动量轮的加载和卸载就可以吸收卫星本体的动量矩，从而达到控制姿态的目的。当外部干扰力矩或推力器的喷气控制过程使动量轮转速达到饱和时，必须对动量轮转速进行卸载控制[5]。由于动量轮卸载采用喷气卸载的方式，会对卫星本体产生附加加速度。目前轨道确定一般采用动力学统计定轨方法[6-7]，而卫星的动力学模型准确与否是影响动力学统计定轨精度的重要因素，因此在轨道确定过程中需要考虑动量轮卸载的影响。微卫星进入环月轨道后，采用对日定向三轴稳定控制模式，动量累积效应明显，一般1～2 d，微卫星动量轮会卸载一次。

2 地月转移段轨道精度评估

2.1 动力学模型

定轨分析采用的计算软件为北京航天飞行控制中心开发的定轨软件系统[8]。轨道解算中的一些计算因素见表1。

2.2 轨道精度评估

为保证任务的实施，微卫星地月转移段的每次轨控前轨道需要满足一定的精度要求。本文定轨精度评估采用星历比较的方法。将任务期间计算的轨道外推至轨控开机点得到的星历与事后计算的精密星历进行比较，并以二者的最大偏差作为衡量定轨精度的依据。任务中，各关键弧段星历精度评估如表2 所示，评估结果为轨道坐标系下的偏差，其中R方向为径向，T方向为横向，N方向为轨道面法向。由表2 结果可知，微卫星自入轨开始至顺利进入工作轨道期间，定轨位置精度在km量级，速度精度在m/s量级。第一次中途修正前由于多个目标航天器同时发射入轨，分配给微卫星的测控资源相对较少，其定轨精度相对较差。近月捕获点附近的定轨速度精度较低是由轨道特性所决定的。近月制动点为以月球为中心引力体的大椭圆轨道的近月点，该处的卫星状态变化迅速，轨道确定和预报的精度相对较低。

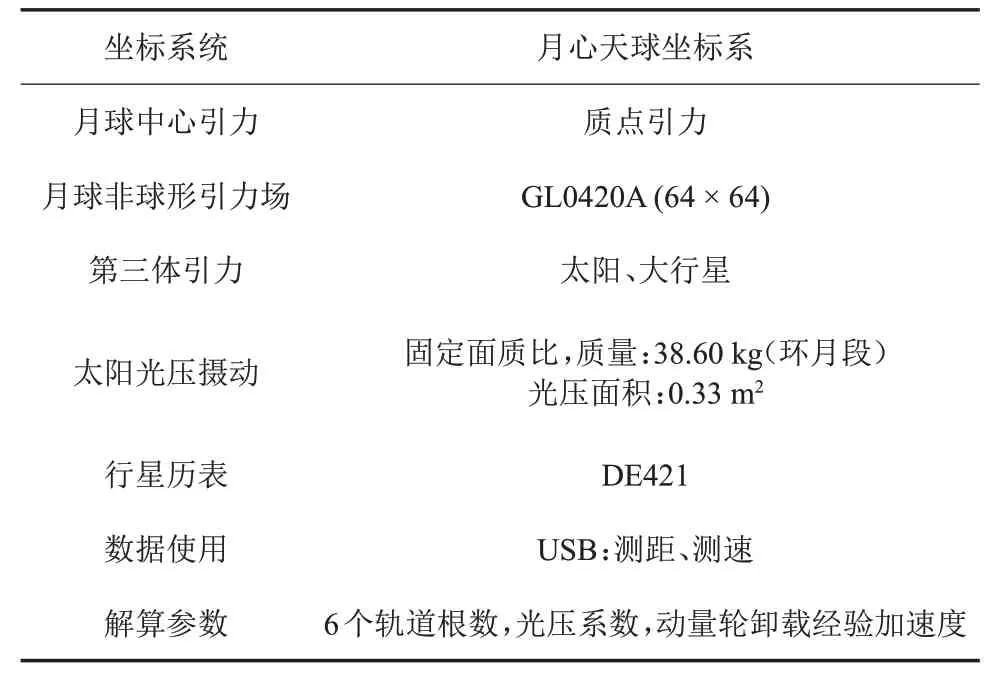
表1 轨道解算因素Table 1 Orbital resolving factor

表2 地月转移段轨道精度评估Table 2 Precision evaluation of Earth-Moon transfer orbit

3 环月段轨道精度评估

3.1 摄动力影响分析

微卫星环月轨道主要受到各行星质点、太阳光压等摄动力的影响。图3 给出了在2018 年07 月27 日9:00初始轨道的基础上外推3天后各摄动源产生的摄动加速度，可以看出，微卫星在环月大椭圆轨道上飞行时，月球、地球的质点引力为主要的摄动源，除此之外，太阳质点、太阳光压以及月球J2 项的摄动影响最大，达到10-6量级，是无法忽略的。地球J2 项、月球固体潮影响较小，约为10-9量级，其它大行星质点摄动影响最小，约为10-12量级。月球质点、J2 项以及固体潮的摄动影响呈周期性，在近月点处最大，在远月点处最小；太阳、地球等其他行星质点引力的摄动影响则相反，在近月点处最小，在远月点处最大。地球J2 项和太阳光压的摄动影响相对平缓，其中，太阳光压摄动影响在阴影区有明显的减小。

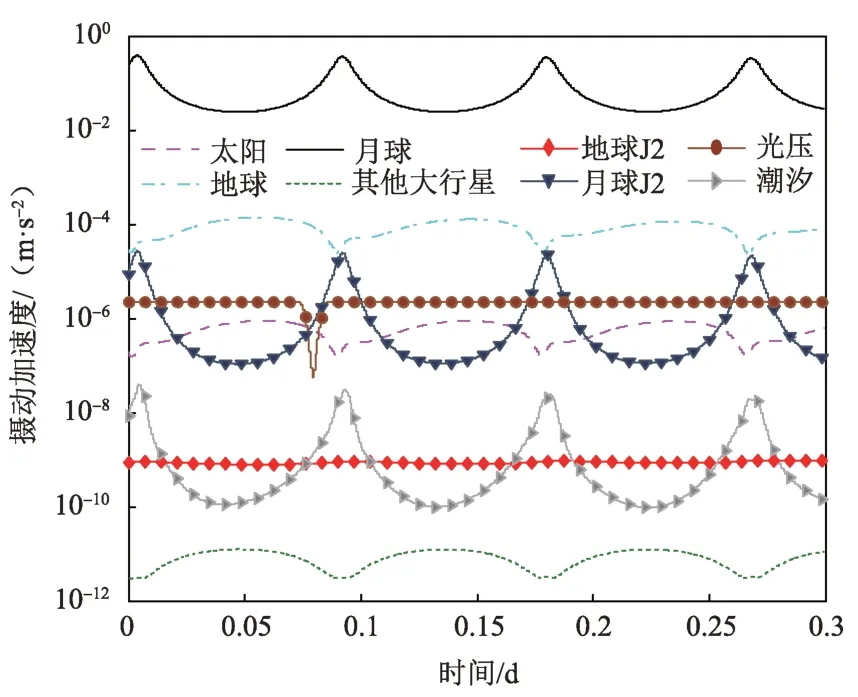
图3 摄动源影响Fig.3 Effect of perturbative force

3.2 动量轮卸载影响分析

以 2018 年 6 月 3 日 7:40 至 2018 年 6 月 6 日 17:00间的观测弧段为例，共有两次动量轮卸载。在不考虑动量轮卸载影响的条件下，求解系统差和光压系数，定轨数据残差如图4所示（图中横坐标为相对于2018年6月3日0时的小时数）。可以看出，不考虑动量轮卸载时残差拟合程度并不理想。因此，将动量轮卸载作为短时间内的常数加速度处理，即在每次动量轮卸载期间，每个方向添加一个常数加速度，而在动量轮卸载期间以外的时间段，此力设置为零，在轨道确定中将动量轮卸载产生的加速度作为未知量进行求解。在考虑动量轮卸载的影响后，定轨数据残差如图5所示。由图4和图5可知，在定轨过程中考虑卸载的影响，定轨过程中解算卸载的加速度，数据拟合程度显著好转。

3.3 数据弧段长度选择

对于微卫星轨道确定来说，由于每天的测量数据较少，较长的数据弧段对于提高该卫星的环月大椭圆轨道的定轨精度有益。然而一般1～2 天，微卫星动量轮会卸载一次，越长的弧段动量轮卸载的次数越多，微卫星的动量轮卸载会产生喷气推力，进而对轨道产生影响，采用长弧段来定轨并不一定能有效提高定轨的精度，因此定轨弧段的选择要综合考虑这两方面的因素[9]。

图4 定轨残差图（不求解动量轮卸载经验加速度）Fig.4 Data residuals of the orbit determination（Without solving wheel-off loading acceleration）

以 2018 年 6 月 1 日 22:50—2018 年 6 月 6 日 17:00间的观测弧段为例，共有3次动量轮卸载。本文对比求解了1 次、2 次、3 次动量轮卸载经验加速度的情况，同时求解了光压系数的系统差，结果如表3 所示。3种求解策略下求解得到的光压系数以及动量轮卸载产生的加速度量级没有显著差异。图6 给出了3种策略下的轨道坐标系定轨误差椭圆（3 倍方差），可以看出，求解2 次动量轮卸载经验加速度比求解1次时定轨误差明显减少，求解3次动量轮卸载经验加速度比求解两次对定轨精度的提高效果并不明显，其它观测弧段的定轨也能得到类似结果。由于采用越长的观测弧段进行定轨计算效率越低，综合考虑精度和计算效率的影响，本文解算弧段为3～4 天，解算卸载次数为2次。

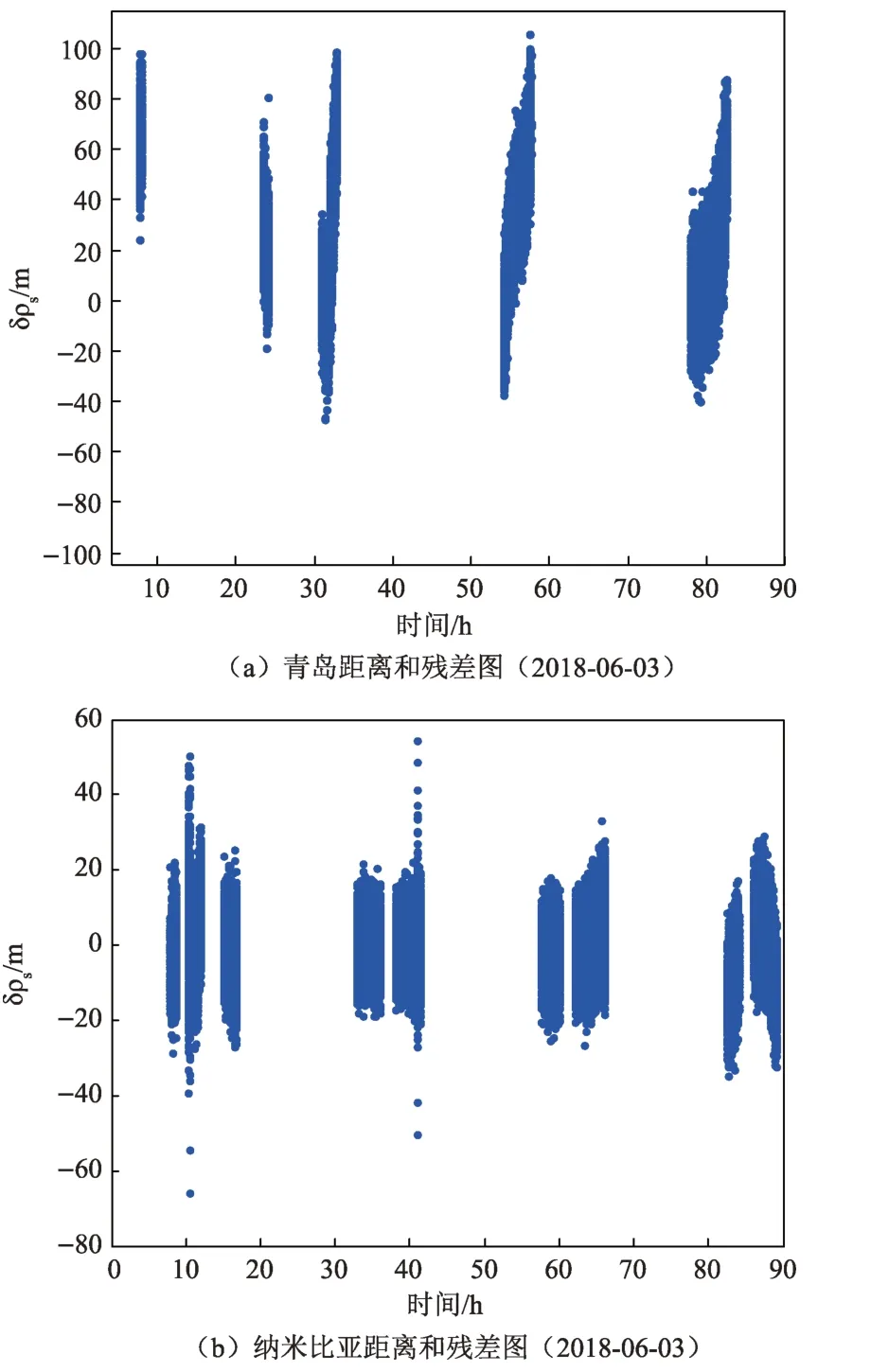
图5 定轨残差图（求解动量轮卸载经验加速度）Fig.5 Data residuals of the orbit determination（Solving wheel-off loading acceleration）

表3 动量轮卸载求解策略比较Table 3 Comparison of the wheel-off loading solving strategies

3.4 轨道精度评估

微卫星环月段的轨道精度分析方法采用两组弧段定轨星历比较重叠弧段的模式[10]。根据上一节的分析，采取求解2次动量轮卸载的策略，取包含两次卸载的最长数据弧段用于轨道确定（例如，取第1次卸载之后和第4次卸载之前的数据用于轨道确定，求解第2 次和第3 次卸载的加速度）。微卫星一般1～2 天动量轮会卸载一次，重叠弧段长度约为2～3 天。将微卫星 2018 年 5 月 30 日—2018 年 7 月 19 日期间的数据进行分组，比较相邻两组弧段定轨得到的重叠弧段星历，得到轨道坐标系下位置和速度偏差的最大值。以第1、2 组比较结果和第2、3 组星历比较结果为例，如图7 所示。可以看出，轨道面法向（N方向）的偏差相对较大，且与轨道周期相关。

图6 定轨误差椭圆Fig.6 Error ellipse of orbit determination

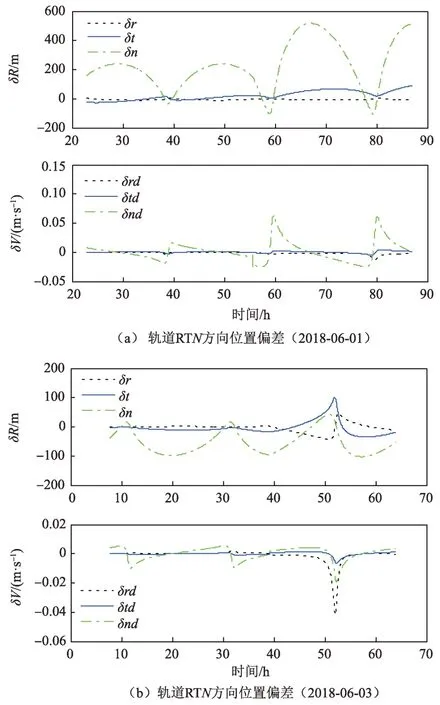
图7 重叠弧段星历比较Fig.7 Comparison of the overlap arc ephemeris

统计重叠弧段星历比较结果，均值和方差结果如表4所示，各组位置和速度偏差总和如图8所示。重叠弧段内位置最大偏差约为1 000 m，速度最大偏差约为0.27 m/s。根据重叠弧段偏差统计结果可知，微卫星环月段定轨位置精度为km 量级，速度精度为dm/s量级。

表4 重叠弧段偏差统计Table 4 Statistical results of the overlap arc ephemeris difference

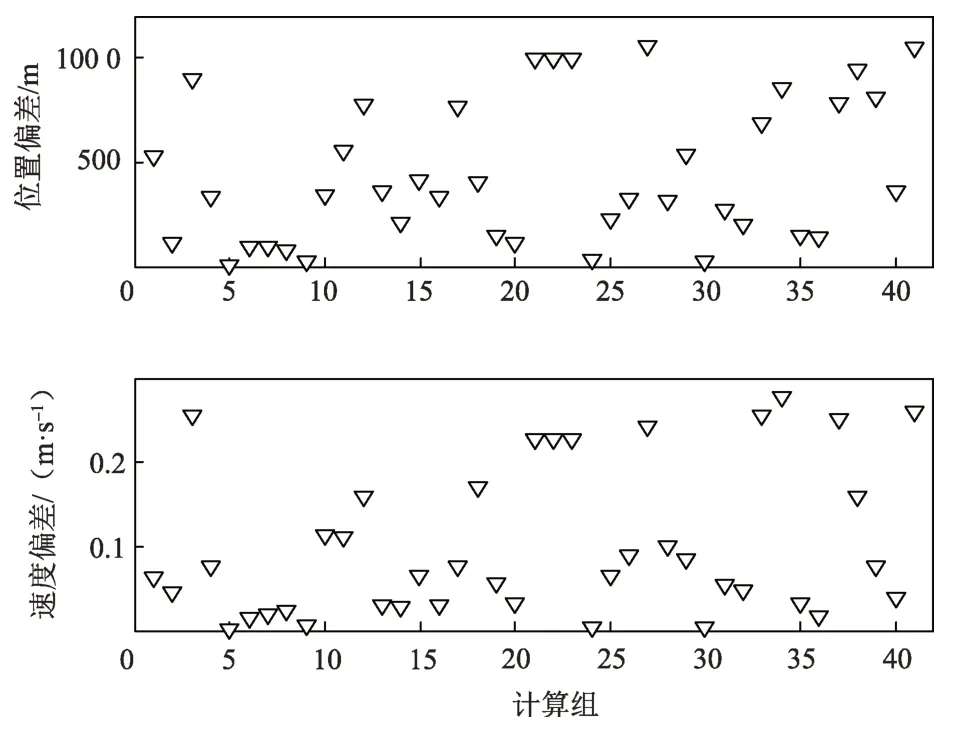
图8 重叠弧段偏差Fig.8 Difference of the overlap arc ephemeris

4 结 论

为实现探测任务效益的最大化，各航天大国纷纷将微纳卫星引入到深空探测项目中。微纳卫星通常通过搭载等形式送入探测轨道。由于深空测控资源有限，分配给微纳卫星的测轨时间较少，有必要对有限测控资源条件下微纳卫星的定轨精度进行分析。

本文采用“龙江2号”微卫星的轨道测量数据对其定轨精度进行分析。对“龙江2号”微卫星飞行任务进行了介绍，给出了参与测轨的测站分布、微卫星动量轮卸载规律等影响测定轨的因素。“龙江2 号”微卫星只有USB 轨道测量数据，且环月段测控资源相对紧张，每天有两站跟踪，共约3～4 h的轨道测量数据。对微卫星地月转移段的定轨精度进行了分析，通过分析摄动力、动量轮卸载以及数据弧段长度的影响，给出了微卫星环月阶段所使用的定轨策略。综合计算效率和计算精度的影响，发现采用求解2次动量轮卸载经验加速度的定轨策略较优。通过重叠弧段比较的模式，给出了微卫星环月段的定轨精度，为后续微纳卫星深空探测的轨道确定提供有益参考。